基于BP神经网络的运量预测模型优化研究

2013-06-11欧阳帆

交通运输研究 2013年12期

欧阳帆

（交通运输部水运局，北京 100736）

0 引言

目前运量预测中应用得比较多的模型优化方法是组合预测模型，它是综合利用各种预测方法，如运输弹性系数法、时间序列分析法、回归分析方法、灰色模型预测等，以适当加权平均形式得出的综合预测模型。其基本思路是：首先分别利用上述几种单项预测模型得到几组基础预测值，通过比较各个预测值与原值之间的误差，给定每组预测值的加权系数，最后通过加权平均得出最终的预测值。这种方法是一种线性的预测模型，存在一定的局限性，而且权重的分配也存在较大的主观性，特别是当实际值与预测值存在非线性关系时，该模型就无法进行预测。

本文将探讨人工神经网络技术在运量预测中的可行性，通过建立非线性组合预测模型，并结合实例分析，研究基于人工神经网络的运量预测模型的实用性。

1 BP神经网络的原理

人工神经网络（Artificial Neural Network）是一种理论化的人脑神经网络的数学模型，是基于模仿大脑神经网络结构和功能而建立的一种信息处理系统，具有高度的非线性，能够进行复杂的逻辑操作和非线性关系实现的系统。BP（Back-Propagation）神经网络是一种前向型神经网络，在人工神经网络的实际应用中，有80%的人工神经网络模型采用的是BP网络或它的变化形式。由于BP算法具有强大的非线性映射能力，在许多实际应用中发挥了重要的作用[1]。

从结构上看，BP神经网络是典型的多层网络，分为输入层、隐层和输出层。其中，隐层可以有多层，层与层之间多采用权连接方式，同一层单元之间不存在相互连接。图1给出了一个三层BP网络结构。BP神经网络模型实现了多层网络学习的设想。当给定网络的一个输入模式时，它由输入层单元传到隐含层单元，经过隐含层单元逐个处理后，传输到输出层单元，由输出层单元处理产生一个输出模式，将误差值沿着连接通路逐层传送并修正各层连接权值。对于给定的一组训练模式，不断用一个个训练模式训练网络，重复前向传播和误差反向传播过程，直到各个训练模式都满足要求。具体过程和算法如下[2]。

步骤1：初始化。输入、输出样本为{xki，dk│k=1，2，…，n；i=1，2，…，ni}。其中，xki为输入的样本数据；dk为样本数据的期望输出；k为样本容量，在样本输入时要对其进行归一化处理，取值范围限制在0～1之间。

步骤2：k=1，把样本对（xki，dk）提供给网络。步骤3：计算隐层各节点的输入xj，输出yj，其中j=1，2，…，nj。

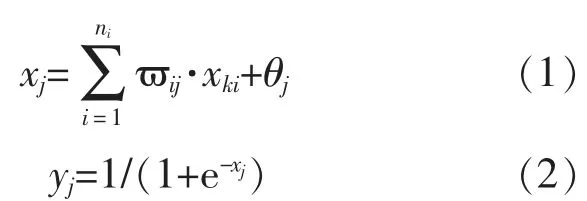
步骤4：计算输出层节点的输入xk，输出yk。

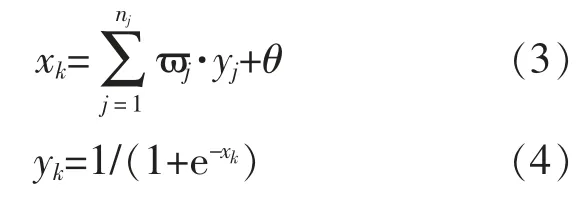
步骤5：计算单样本点误差Ek的变化率。

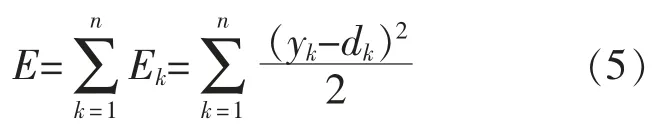
步骤6：修正各连接线的权值和阈值，计算公式略。

步骤7：k=k+1，重复步骤2～步骤6，直至网络全局误差E小于预先设定的一个较小值或学习次数大于预先设定的某个值，结束学习。

步骤8：对己经学习好的BP网络加载检验样本，输出分析结果，至此BP算法运行结束。

目前，BP神经网络模型的计算可以利用DPS、MATLAB等数据处理软件来完成。

图1所示为一个三层的BP网络模型。

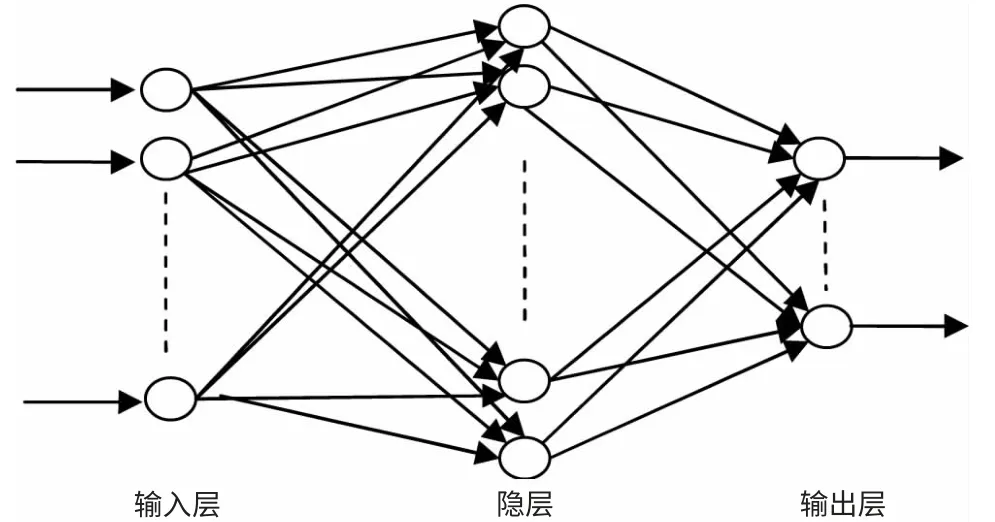
图1 一个三层的BP网络模型

2 基于BP神经网络的预测优化原理

利用BP神经网络优化进行预测优化的思路与组合预测模型基本相同，只是加权通过BP神经网络来完成。首先将各种单项预测方法的预测值作为BP神经网络的输入层，将代表相应年份的实际值作为输出层，然后用足够多的预测样本训练这个网络，使不同的输入向量得到相应的输出值，从而在各参加组合的单项预测方法的预测结果与实际值之间建立一种非线性映射关系，经过不断的学习及测试，满足一定的精度要求之后，该网络就可以作为非线性组合预测的有效工具，用于预测并得到最终预测结果[3]。

本文以1990～2009年全国水路货物运输量为实例进行具体说明。基础数据见表1，表中数据来源于1991～2010年出版的《中国统计年鉴》。

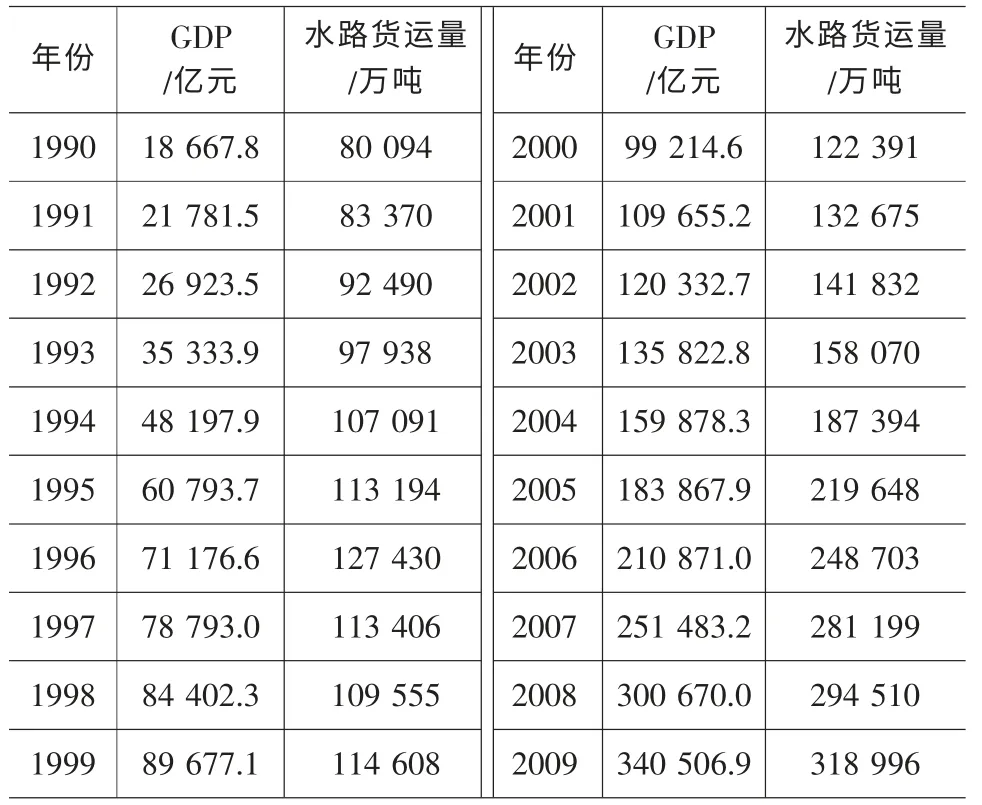
表1 1990～2009年全国GDP与水路货运量指标[4-23]

2.1 单项预测模型

本文选取一元线性回归模型、一次指数平滑法和灰色系统GM（1，1）模型分别建立预测模型，对原始数据进行预测，预测模型如下：

a）一元线性回归模型（以GDP作为自变量，运量作为因变量）；

b）一次指数平滑法，取α=0.98进行计算；

c）灰色系统GM（1，1）模型。

预测结果见表2。

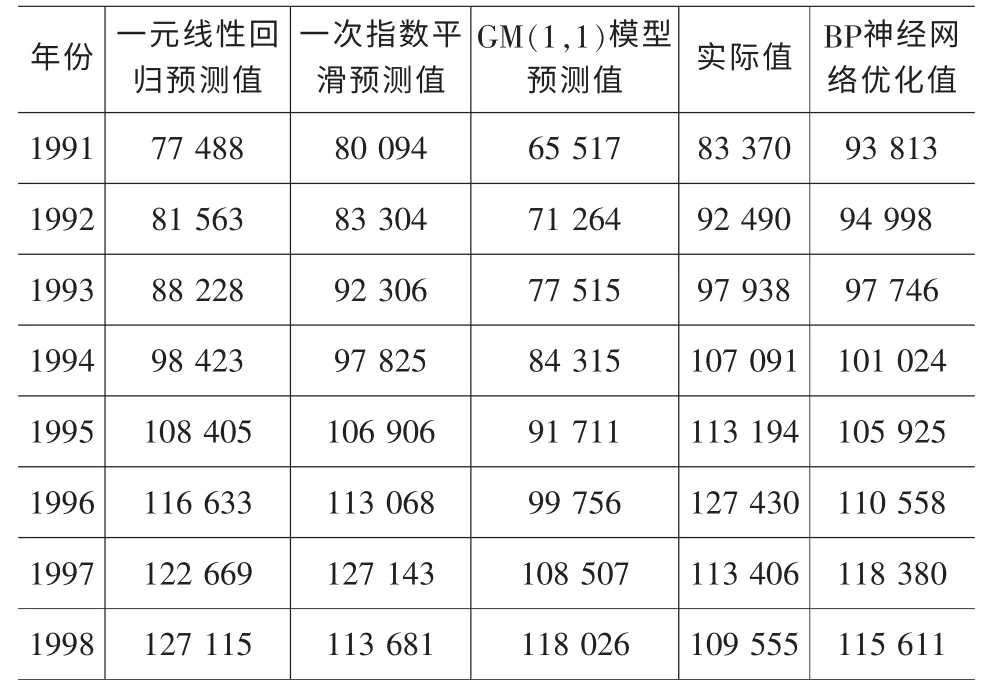
表2 各预测模型的运量预测值及优化值单位：万吨

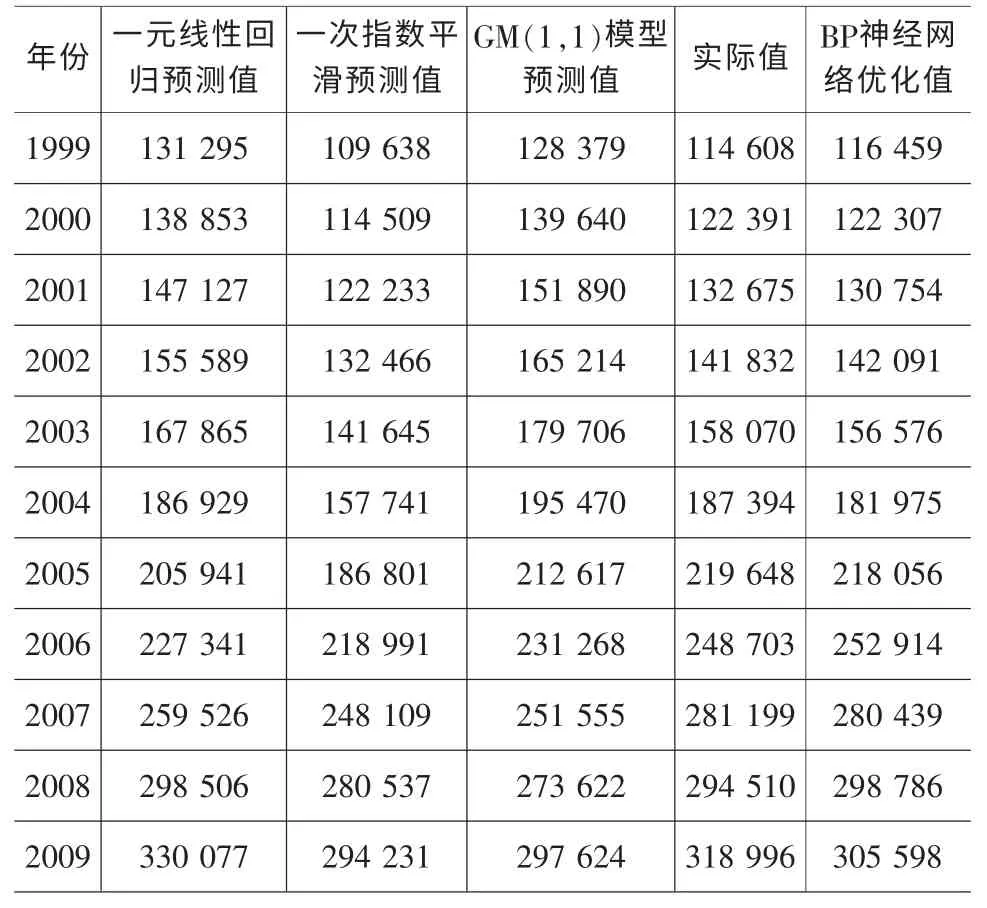
表2（续）

2.2 BP神经网络优化

利用DPS统计软件自带的BP神经网络模型进行计算，将2.1中3个模型的预测数据（1991～2009年）作为输入量，选择“标准化变换”（归一化），隐层神经元数量取30（经多次训练，发现神经元为30个左右时精度相对较高），训练过程见图2。训练完毕得到最终预测优化结果见表2，残差为0.00082。由于得到的各层神经元的权重太多，这里就不再一一列举了。

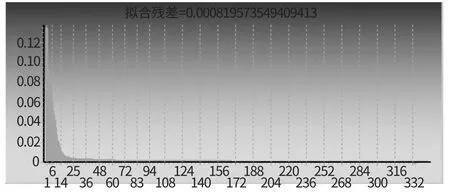
图2 预测模型优化的训练过程

2.3 误差检验

通过计算标准误差与平均绝对百分比误差，来反映不同模型的精确程度，计算方法如下[24]。

标准误差（均方误差）：

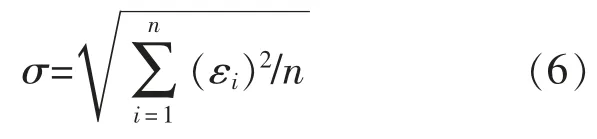
平均绝对百分比误差：

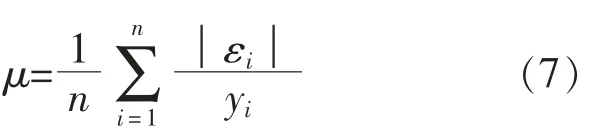
式中，σ为标准误差；μ为平均百分比误差；ε为单个预测值与实际值之间的误差。

计算结果见表3。

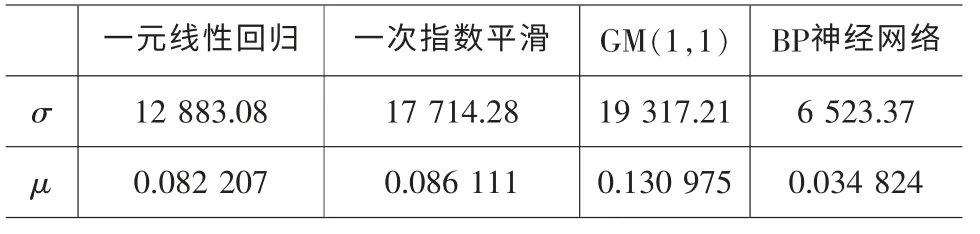
表3 各预测模型的标准误差

根据表3可知，采用基于BP神经网络优化的预测模型计算得出均方误差为6523.37，平均绝对百分误差为0.034824，均小于各单项预测方法的误差值。由此证明，采用基于BP神经网络的运量预测模型优化了单项预测模型，提高了预测精度。

3 结论

本文论述了BP神经网络的理论，以及基于BP神经网络的运量预测模型的优化问题。以时间序列分析法、回归分析方法、灰色模型预测方法为基础，以1990～2009年全国水路货物运量为样本数据，充分利用BP神经网络的非线性映射能力，建立实际运量发展趋势与各种单项预测方法的有用信息之间的一种复杂的关联，并通过数据的学习和训练实现预测精度的提高。实例分析证明，基于BP神经网络的运量预测优化模型，能有效克服单个预测方法的局限性，更好地反映实际运量的发展情况，这种方法在运量预测中是可行的。但是，基于BP神经网络进行预测优化是以大量的历史数据为前提的，在数据样本较少的情况下，预测精度可能会受影响。

[1]易帆.神经网络预测研究[D].成都：西南交通大学，2005.

[2]张庆年.交通运输系统分析与优化[Z].武汉：武汉理工大学，2005.

[3]宋玉强.人工神经网络在时间序列预测中的应用研究[D].西安：西安建筑科技大学，2005.

[4]中华人民共和国国家统计局.中国统计年鉴[M].北京：中国统计出版社，1991.

[5]中华人民共和国国家统计局.中国统计年鉴[M].北京：中国统计出版社，1992.

[6]中华人民共和国国家统计局.中国统计年鉴[M].北京：中国统计出版社，1993.

[7]中华人民共和国国家统计局.中国统计年鉴[M].北京：中国统计出版社，1994.

[8]中华人民共和国国家统计局.中国统计年鉴[M].北京：中国统计出版社，1995.

[9]中华人民共和国国家统计局.中国统计年鉴[M].北京：中国统计出版社，1996.

[10]中华人民共和国国家统计局.中国统计年鉴[M].北京：中国统计出版社，1997.

[11]中华人民共和国国家统计局.中国统计年鉴[M].北京：中国统计出版社，1998.

[12]中华人民共和国国家统计局.中国统计年鉴[M].北京：中国统计出版社，1999.