弹道导弹拦截仿真建模技术研究

梁 慜

(中国电子科学研究院，北京 100041)

0 引 言

弹道导弹射程远、速度快、突防能力强、威力大等优越性能，使其成为现代战争中最具威胁的攻击性武器之一。为建立一个高效的弹道导弹防御系统，必须对来袭弹和拦截弹的弹道进行仿真分析和研究。

弹道导弹的弹道分为助推段、自由段和再入段，自由段很长，占弹道绝大部分。近程弹道导弹和中远程弹道导弹的自由段弹道分别用抛物线弹道和椭圆弹道建模［1］。助推段弹道和再入段弹道则采用同一方程建模，助推段弹道采用简化模型模拟弹道导弹的变加速转弯过程，再入段弹道在简化大气模型下建立弹头的简化运动学方程。拦截弹采用复合制导，末制导采用比例导引法建立弹道方程，与来袭弹弹道方程联立，可以仿真出拦截遭遇时间等重要参数。此外，给出拦截仿真误差表达式，并分析了其对拦截仿真精度的影响，提高了仿真的可信度。

1 坐标系

1.1 建模坐标系

除中远程弹道导弹自由段弹道方程外，其他弹道方程均建立在该坐标系下。建立以打击点为坐标原点o 的平面直角坐标系o－xyz，oy 轴为原点与地球的切线，指向发射点方向，oz 轴垂直于oy 轴，方向由地心指向外。来袭弹与拦截弹的坐标分别为(xM，yM，zM)和(xI，yI，zI)。弹道方程解算后，通过坐标转换，可将弹道变换到任意坐标系下。

1.2 地心惯性坐标系

中远程弹道导弹自由段弹道(椭圆弹道)方程建立在地心惯性坐标系下，定义为:以地球地心为坐标原点o，xoy 平面在赤道平面上，ox 轴正向指向格林尼治子午线与赤道的交点，oz 轴指向地球北极，与地球极轴重合。

2 弹道导弹弹道建模

2.1 弹道导弹助推段弹道方程

假设弹道导弹射程L，关机点高度h0，关机点弹道倾角θ0，再入点高度h1，再入角θ1均已知，取典型值，可得关机点速度v0和关机时间t0［2］

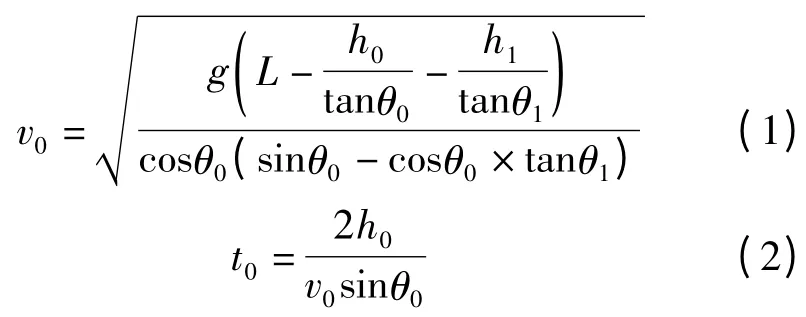
在建模坐标系o－yz 内建立助推段弹道方程组［2］

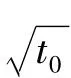
2.2 弹道导弹自由段弹道方程

2.2.1 近程弹道导弹自由段弹道方程

在自由段，弹头在接近真空的大气环境内惯性飞行，空气阻力相比于地心引力可以忽略不计，作用在弹头上的力主要是地心引力，其运动轨迹可以简化为二次抛物线［3］，在建模坐标系o －yz 内建立自由段弹道方程组，为

式中，g 是重力加速度。

自由段飞行时间为

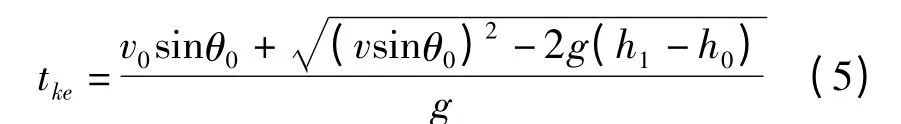
2.2.2 中远程弹道导弹自由段弹道方程

射程1000 km 以上的战术弹道导弹的自由段弹道近似为椭圆轨道，采用天体力学一致的参数，即“轨道根数”来描述。根据文献［4］中的计算方法得到六个轨道参数:半长轴a，偏心率e，轨道倾角i，升交点角距Ω，近地点角距ω，过近地点时刻tp。在地心惯性坐标系下建立自由段弹道方程组，为

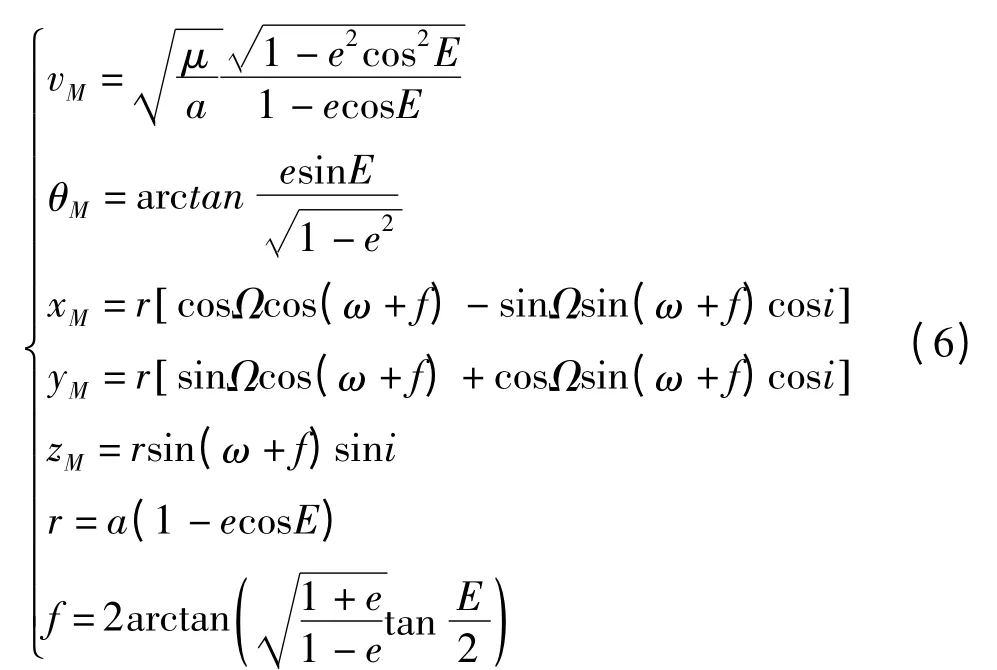
式中，r 是弹头的地心距;f 是真近地点角;E 为偏近地点角，根据开普勒定理，由式(7)迭代求出

其中μ = 3.986 ×1014 m3/s2。

2.3 弹道导弹再入段弹道方程

在再入段，弹头所受的主要是地心引力和大气阻力［5］，在建模坐标系o－y 内建立再入段弹道方程组，为

式中，m 是弹头质量;R 是地球等效半径;XF是空气阻力，且

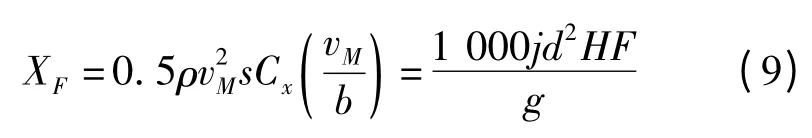
式中，ρ 是空气密度;s 是导弹横截面积;b 是音速;Cx(vM/b)是马赫数对应的标准阻力系数;j 是弹形系数;d 是导弹底部直径;F(v)是阻力函数，F(v)=4.75 ×10－4× v2Cx(vM/b);H(h)是无因次空气比重，其经验公式为

2.4 拦截弹弹道方程

对多个来袭弹进行威胁排序［6］后实施拦截，拦截弹发射一秒钟内为无控段，模拟飞行和自稳定过程，此后转入中制导段，根据基于零脱靶量的制导律［7］导向来袭弹，当距离来袭弹约15 km 时，末制导段开始，根据比例导引律大角度侧向拦截来袭弹。

末制导中，假设拦截弹与来袭弹在每个时间采样间隔内做匀速直线运动，且在同一平面中运动。比例导引法［8］差分方程图解分析，如图1 所示，k－1时刻拦截弹与来袭弹的空间位置分别为Ik－1和Mk－1，坐标分别为［xI(k－1)，yI(k－1)，zI(k －1)］和［xM(k－1)，yM(k －1)，zM(k －1)］，k 时刻拦截弹与来袭弹的空间位置分别为Ik和Mk，坐标分别为［xI(k)，yI(k)，zI(k)］和［xM(k)，yM(k)，zM(k)］，IkMk∥IkB，根据几何知识，有

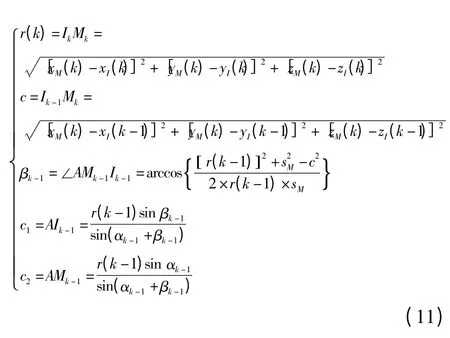
式中，SM是来袭弹在一个时间采样间隔内运动的距离，SM= vM(k－1)。

由于拦截前期拦截弹与来袭弹之间的距离比较远，假设拦截弹在k 时刻不运动，来袭弹运动到Ik，拦截弹根据来袭弹新位置Ik进行Δqk预报

图1 比例导引法图解

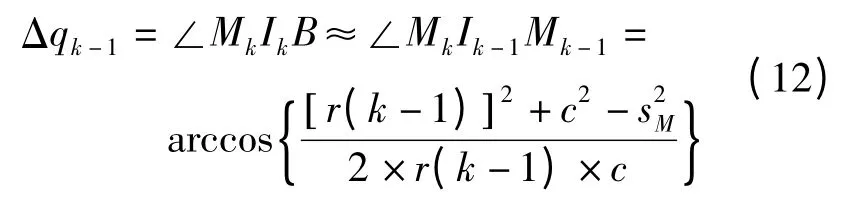
拦截弹比例导引法的差分方程为

式中，SI是拦截弹在一个时间采样间隔内运动的距离，SI= vI(k－1)。

拦截弹与来袭弹比较接近时，用∠AIk－1Mk－1近似Δqk－1时误差比较大，需要对其进行校正

3 数值仿真

联合方程(1)～(10)与方程(11)～(15)，可以仿真出来袭弹和拦截弹的完整弹道，包括位置、速度、倾角等信息，以及拦截遭遇时间。

建模坐标系下近程弹道导弹拦截曲线和地心惯性坐标系下中远程弹道导弹拦截曲线，如图2 和图3 所示。

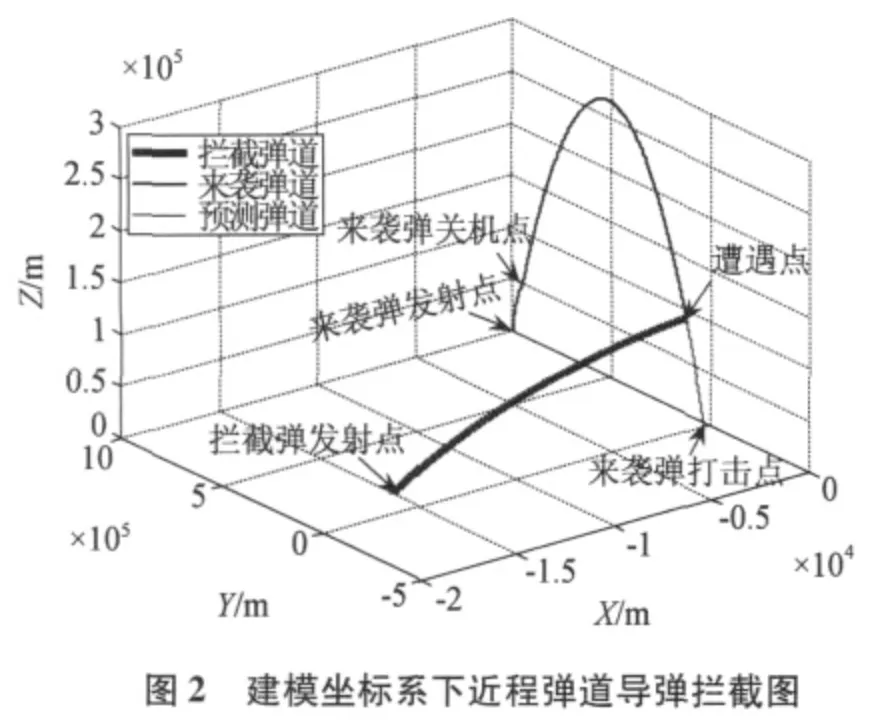
由于采用数字仿真，来袭弹和拦截弹无法完全遭遇，需要设定一个误差值ε 来判断拦截是否成功，若弹道导弹与拦截弹的相对距离小于误差值，拦截成功，否则，拦截失败。拦截仿真误差表达式为

从式(16)中可以看出，拦截仿真误差与采样间隔和遭遇时刻来袭弹与拦截弹的相对速度有关。相对速度一定的情况下，采样间隔与拦截仿真误差的关系图如图4 所示，采样间隔越小，拦截仿真误差越小，但仿真计算量越大。

遭遇时刻来袭弹和拦截弹的相对速度很难获知，只能对其进行估计，当采样间隔一定时，若估计值过小，会使判断拦截成功的概率降低;若估计值过大，会使遭遇时间提前，判断拦截成功的概率升高。因此，需要对遭遇时刻来袭弹和拦截弹的相对速度有适当的估算，才能保证拦截仿真的可信度。

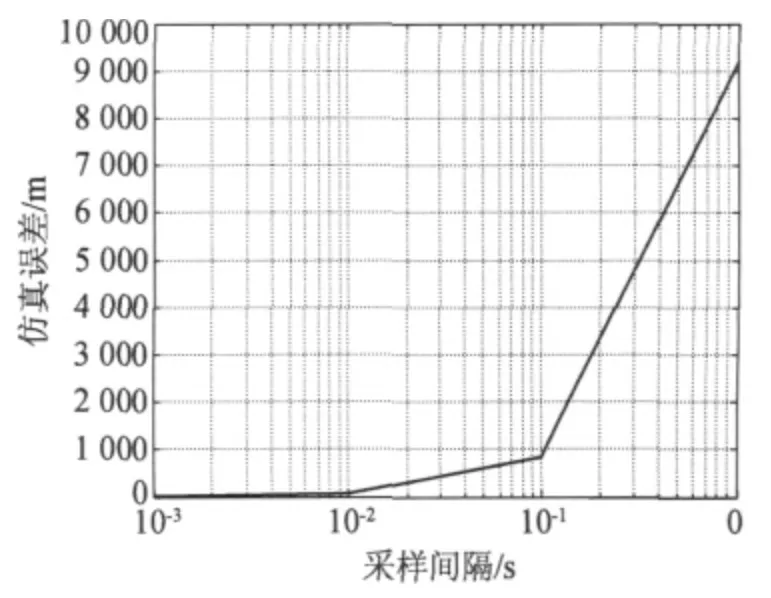
图4 不同采样间隔下的拦截仿真误差

4 结 语

对弹道导弹从发射到被拦截的全过程进行了一体化建模仿真，给出了拦截仿真误差表达式，分析了其对仿真精度的影响，提高了拦截仿真的可信度，为预警探测、中段拦截、末段拦截等反导作战研究提供有效支撑。

［1］贾沛然，沈为异. 弹道导弹弹道学［M］. 长沙:国防科技大学出版社，1987.

［2］李毅，刘晶，邵锡军.战术弹道导弹弹道仿真建模技术研究［J］.弹箭与制导学报，2011，31(2):145-148.

［3］ 胡传俊，杨恢先. 弹道导弹被动段弹道方程与仿真［J］.弹箭与制导学报，2010，30(4):131-133.

［4］霍伟，王晓钧. 基于弹道仿真的反导系统分析［J］. 中国电子科学研究院学报，2009，4(5):507-510.

［5］汤阳春，娄寿春，赵辉.战术弹道导弹再入段弹道仿真设计［J］.弹箭与制导学报，2006，26(2):98-99.

［6］杨进佩，王俊，梁维泰. 反导作战中的目标威胁排序方法研究［J］. 电子科学研究院学报，2012，7(4):432-436.

［7］王婷，周军.PAC-3 拦截弹建模与仿真研究［J］.系统仿真学报，2007，19(20):4642-4645.

［8］马其东，王磊，金钊. 比例导引法三维弹道仿真分析［J］.战术导弹技术，2008(3):93-96.