基于Kriging与IDW融合算法的氧化带DTM拟合方法*

李 迪 胡乃联 李国清 杨 桦

（金属矿山高效开采与安全教育部重点实验室）

基于Kriging与IDW融合算法的氧化带DTM拟合方法*

李 迪 胡乃联 李国清 杨 桦

（金属矿山高效开采与安全教育部重点实验室）

氧化矿带取样数据属于广域离散型数据，而传统插值方法对于离散型数据不能很好地拟合，误差较大。为此，基于Kriging法的区域化变量及距离幂次反比法（IDW），提出了将二者融合的新算法，并以国内某大型露天钼矿为例进行研究，得出该算法简单易行，且能大幅提高氧化带数字地面模型（DTM）拟合精度的结论。

氧化带 Kriging IDW DTM拟合

氧化矿是金属矿床受氧化作用形成的氧化带中的矿石。矿石受氧化作用后，其矿物组分、结构、构造均产生明显变化，因而在加工利用时须采用不同于原生矿的方法与工艺流程。地质勘查时，需要通过系统的采样和物相分析来确定氧化带的界线及深度。当矿床的氧化矿石占到总储量的一定比例时，还必须进行选矿试验，圈定范围。因而氧化矿量的多少是选矿方法择取的主要影响因素之一。为选择合理的选矿方法与工艺流程，通常需要精确计算氧化矿量。从技术经济的角度看，对于氧化量占到一定比例的某些贵金属矿，宜采用堆浸方式进行选矿处理，且氧化矿量决定了堆浸计量、规模等相关参数。因此，精确计算氧化矿量对于最大限度地开发利用矿产资源具有重要意义。

氧化带是区分氧化矿与原生矿的重要依据。氧化带的数字地面模型（DTM）精确程度对氧化矿量的计算具有重大影响，为此，迫切需要对建立精确氧化带模型的方法进行深入研究。近年来，随着可视化研究不断深入，图形仿真技术普及矿业领域，矿山数字化已成必然趋势。在矿业软件中，建立氧化带DTM，能自动识别区分氧化矿与原生矿，对后续计算氧化矿量等相关操作必不可少。然而，现阶段用于建立氧化带DTM的方法较少，且结果并不理想，主要原因如下：其一，氧化率化验数据属广域离散型数据，生成DTM过度生硬，拟合误差大，需要进行插值计算；其二，传统插值方法对于离散型数据拟合效果较差，导致插值精度不高；其三，氧化带插值后与地表、原生矿带DTM矛盾时如何处理需要进一步讨论。为此，本研究提出Kriging与IDW融合算法，并以国内某大型露天钼矿进行空间插值计算，借助3DMine软件生成插值拟合模型。

1 IDW算法与K riging算法概述

空间点插值计算方法很多，其中常用的有IDW与Kriging插值算法［1］。

随各行业数字化的发展，IDW（Inverse Distance Weighted）以其原理简单、插值过程快速高效的特点，广泛应用于各领域［2］。国内外诸多软件引入IDW作为内部插值计算方法，如矿业软件3Dmine、MicroMine、Surpac，遥感软件ERmapper［3］，GIS系列软件ArcGis、MapGis［4］及统计分析软件等。

IDW是一种常用而简便的空间插值方法，它以插值点与样本点间的距离为权重进行加权平均，离插值点越近的样本点赋予的权重越大.该方法对于未采样点的估计值是未采样点属性真值的无偏估计。然而，IDW法单单只考虑了距离与待估值之间的关系，在本研究所要插值计算的氧化带模型中并没有考虑到空间地质因素，即氧化带成因所造成的空间相关性，因而该方法具有一定的弊端。为提高估值精度，人们广泛应用Kriging进行估值。

Kriging法是以矿化空间结构理论为基础，区域化变量为核心，变异函数为工具的数学地质方法，是地质统计学中的核心方法。地质统计学发展近60 a，在国内外各学科领域有着广泛的应用。在矿业领域，地质统计学不仅广泛应用于资源储量计算，在其他矿业活动，如异常评价［5］、找矿勘探［6］、矿体圈定［7］采矿设计［8］及地学科研［9］等方面也具有明显的优越性。

Kriging相比于IDW最突出的优势是区域化变量理论，区域化变量理论将地质因素加入到插值计算中，使得插值运算不再是纯数学问题，而是与空间地质相关的地质统计学问题。本研究的插值对象是氧化率取样点标高，即Z值，以Z（xu，xv，xw）作为区域化变量。区域化变量能够反映地质变量的结构性及随机性。当空间点x位置确定后，该点标高Z（x）为随机变量，空间两不同点x、x＋h处标高Z（x）、Z（x＋h）具有某种程度的自相关性，这种自相关性依赖于分隔两点的距离h和地质构造、矿化规律，体现了氧化矿成矿过程的某种联系性，即区域化变量的结构性。

Kriging法全面应用数理统计理论，遵循无偏估计和最优估计原则，考虑了地质因素对差值计算的影响，因而估算精度相对较高。然而，Kriging的最大缺陷是其平滑效应［10］，这种平滑效应使得氧化面高程均化，严重影响插值精度。为提高模型拟合的精确度，还需进一步改进算法。

针对2种算法各有优缺点的现状，本研究考虑将2种算法融合。

2 基于K riging与IDW融合算法的数学模型

基于上述2种插值方法的优缺点，本研究提出Kriging与IDW融合算法，将地质统计学中的核心优势——区域化变量理论引入IDW。本研究的插值对象虽为氧化带标高，但能体现氧化面成矿规律的是其氧化率属性，因而Kriging中的变异函数拟合对象是氧化率属性。首先通过Kriging方法中针对氧化率属性的变异函数拟合找到插值点间的空间地质关联，Kriging中的空间地质关联集中体现在插值权重等值面构成的搜索椭球体上，通过Kriging变异函数的拟合找到搜索椭球体定义参数，包括椭球体搜索半径，椭球体倾角、方位角、倾伏角，以及主轴、半主轴、短轴之间的比率等。最后在IDW中对氧化面标高属性的插值过程中根据Kriging求得的搜索椭球体作为插值中搜索样品对的方式，继而进行IDW插值计算。这种融合算法能够有效避免Kriging的平滑效应与IDW中缺乏地质成因关联的不足。

IDW法用于插值的基本公式为

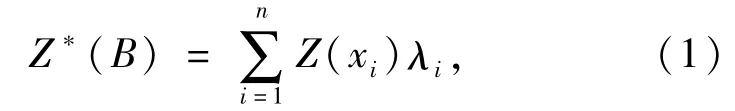
式中，Z*（B）为待估点属性值，这里指待估点氧化带标高；Z（xi）为已知采样点标高；λi为已知点权重。依据IDW法的基本思想，确定权重λi的方法为

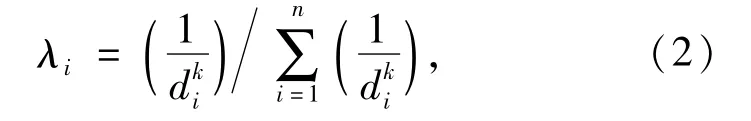
式中，di为待估点与已知点间距离；k作为di的幂指数，其取值由具体情况确定，通常可以取1，2，3等整数。

Kriging方法中使用变异函数来描述区域化变量的空间结构性变化和随机性变化，通过变异函数拟合寻找椭球体搜索参数。氧化面取样点氧化率R（x）在点x、x＋h处增量方差的一半，即R（x）在该方向上的半变异函数。

在实践中，把由有限实测样品值构成的变异函数称之为实验变异函数，记为g*（h）。

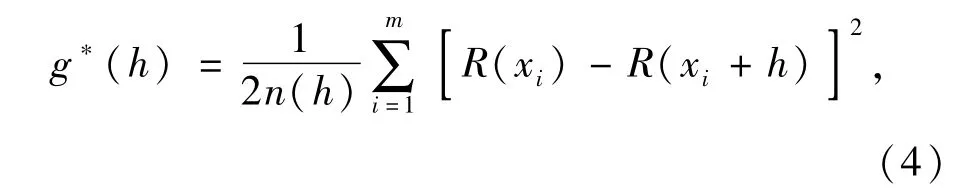
式中，n（h）为相距h的样品对数；R（xi）、R（xi＋h）分别为xi、xi＋h处的氧化率化验值。

Kriging方程组求解思想是使估计方差最小［11］，经过Kriging法求解寻得最优拟合结果，得到相应的搜索椭球体基本参数，并将该系列参数带入到IDW中，确定IDW中搜索样品对的方式，最后由式（1）、式（2）、式（3）求得插值结果。

3 工程应用

3.1 工程背景

某露天钼矿采矿权面积4.6 km2，开采深度640～0 m标高，为目前国内最大单一钼矿床。根据地质勘探报告，得到如下氧化带信息：该矿将勘探工作中氧化钼含量与全钼含量的比值（氧化率）≥10%的钻孔样品定义为氧化带。矿体氧化带最大深度51.93 m，平均16.82 m；氧化矿石最厚17.50 m，平均厚4.28 m；在松散盖层以下，氧化带平均氧化率最高76.45%，最低10.02%，平均37.42%；矿化岩石氧化率，一般由地表向深部逐渐降低。在地表，氧化率最高达100%，向深部最低为10.2%。局部处在后期断裂构造带上的氧化矿或矿化岩石，氧化率呈现高低相间分布，变化较大。简言之，矿体氧化带不甚发育，一般顺地形起伏而变化，呈似层状，但在后期断裂构造带附近，不仅氧化深度较大，且氧化率值变化无明显规律。

3.2 建立氧化带DTM

氧化带上表面接近地表，区分氧化矿与原生矿的主要依据是氧化带下表面（即下氧化面）。这里主要研究下氧化面DTM。本次研究共收集氧化率数据245个。首先将氧化率化验数据导入数据库，在常规数据库基础上新建oxidation表。oxidation表结构如表1。

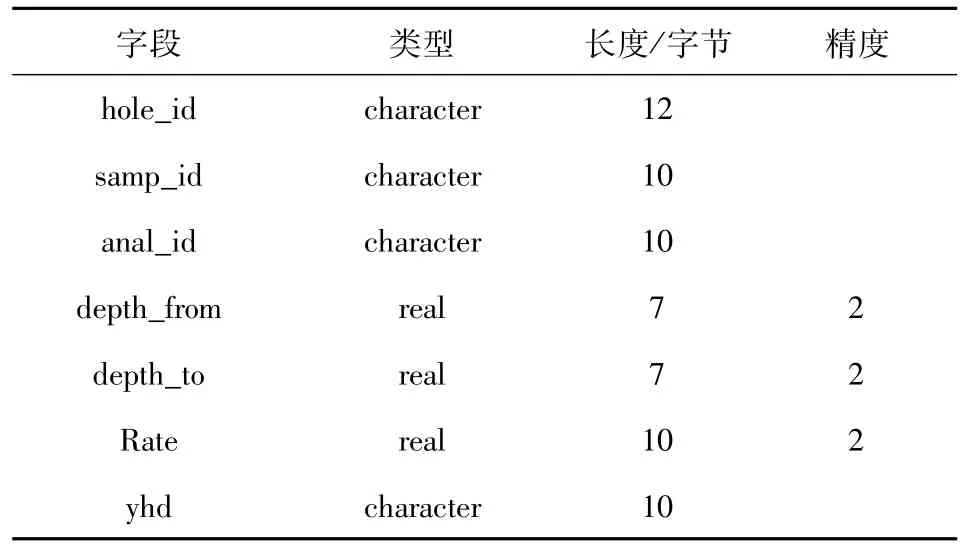
表1 钻孔氧化率数据oxidation结构

根据化验点已知氧化率生成氧化面与原生矿面DTM，即分别由氧化率大于10%与小于10%的点生成，如图1、图2所示。

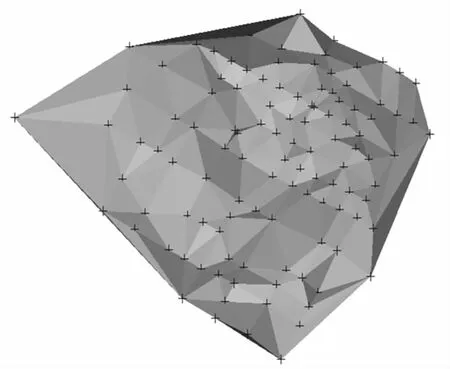
图1 氧化面初步DTM

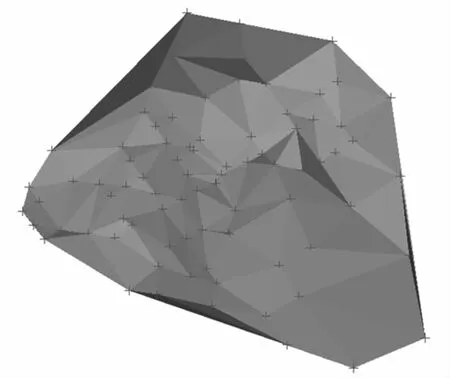
图2 原生矿面DTM

氧化率大于10%的化验取样点被认为是氧化带的组成部分，即插值计算中的已知点。针对已知点采用本研究提出的Kriging与IDW融合插值法。首先根据氧化率组合样建立变异函数模型，继而进行结构分析拟合，图3显示了主轴变异函数的拟合状况，半主轴、短轴拟合过程类似，这里不再赘述。最后得到基台值90.584 01，变程284.894，方位角139°，倾角10°，倾伏角0°，主轴与半主轴、短轴之比分别为1.27、1.00，椭球体如图4所示。最后将得到的搜索椭球体应用到IDW中，作为IDW样品对的搜索方式进行插值，由插值点与原样品点共同参与生成下氧化面DTM，如图5所示。

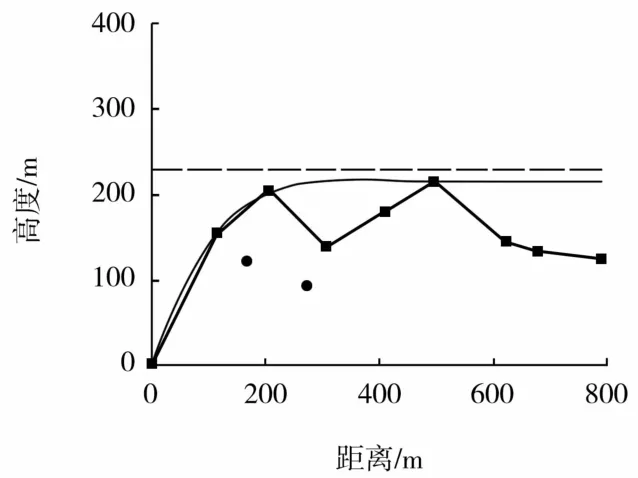
图3 变异函数主轴拟合过程

3.3 模型修正

由于氧化面不能穿过地表，并且不能与化验小于10%的样品点矛盾，这里调入地表DTM与原生矿面DTM，对插值后的氧化带模型进行修剪、校正，其过程如图6、图7所示。

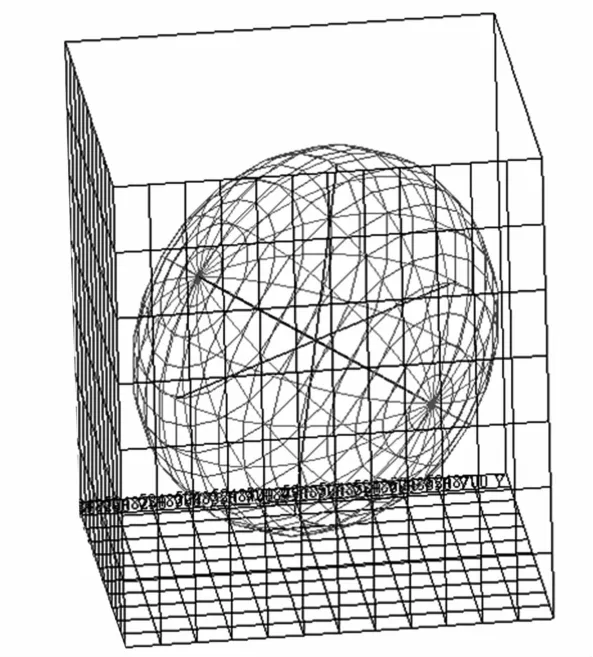
图4 K riging拟合的各向异性椭球体

图5 插值后的实体模型

图6 氧化面与地表相交处理

图7 氧化面与原生矿面相交处理

3.4 结果分析

为进一步验证融合算法的准确性，研究使用Kriging法对化验点进行插值计算，并针对原化验点将插值结果与融合算法进行对比（如图8）：Kriging插值具有明显的光滑效应，其结果均化明显，对原取样点变化趋势的拟合效果较差，而融合算法所得插值结果更加服从原始数据，并较为准确地拟合出其趋势效果。

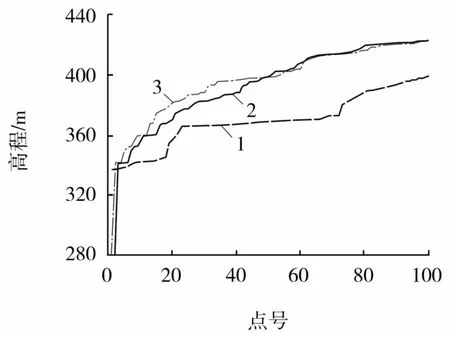
图8 K riging法与融合算法结果对比

图9反映了插值前后氧化面的变化，经对比发现插值计算得到的氧化带DTM相较于插值前的模型更加平滑、精确，贴近实际，一定程度扩展了氧化面面积，能够有效切割矿体，并由地表模型、原生矿面模型加以校正，增加模型拟合精度，为求取氧化矿石量提供了准确保障，对该矿山后续选矿方式及矿石堆存方式的择取具指导性意义。

图9 氧化面界面对比

4 结 论

（1）氧化带化验数据属广域离散型数据，生成氧化带表面过渡生硬，其连接方式导致结果准确性差，面积有所限制。

（2）将Kriging方法与IDW法融合，针对广域离散型数据进行插值计算，能够有效避免Kriging的平滑效应与IDW中缺乏空间地质因素的不足，提高氧化带表面拟合精度。

（3）该方法借助3DMine矿业软件插值计算，操作相对便捷。

［1］张伊丽.基于CUDA的泛kriging算法的研究与设计［D］.北京：中国地质大学，2012.

［2］李章林，王 平，张夏林.距离幂次反比法的改进与应用［J］.金属矿山，2008（4）：88-92.

［3］丁建华，肖克炎，娄德波，等.大比例尺三维矿产预测［J］.地质与勘探，2009（6）：729-734.

［4］罗周全，张 保，刘晓明，等.矿体品位和储量统计分析的三维可视化方法［J］.有色金属，2008（5）：23-27.

［5］Kringe D G.Some basic considerations in the application of geostatistics to valuation of ore in south African gold mines［J］.The South African Institute of Mining and Metallurgy，1976，76（9）：383-391.

［6］潘国成，李秀峰.地质统计学储量估算方法在矿业中应用的若干实际问题（一）［J］.国外金属矿山，1996（7）：7-12.

［7］潘国成，李秀峰.地质统计学储量估算方法在矿业中应用的若干实际问题（二）［J］，国外金属矿山，1996（8）：5-9.

［8］李晓晖，袁 峰，贾 蔡，等.基于地统计学插值方法的局部奇异性指数计算比较研究［J］.地理科学，2012（2）：136-142.

［9］李 健，吴顺川，高永涛，等.基于Kriging与Closest Point融合算法的边坡岩土层界面拟合［J］.北京科技大学学报，2012，34（5）：500-505.

Oxidation Belt DTM Fitting M ethod Based on K riging and IDW Nesting Algorithm

Li Di Hu Nailian Li Guoqing Yang Hua
（State Key Laboratory of High-Efficient Mining and Safety of Metal Mines，Ministry of Education）

Sampling data of oxidation belt iswide and discrete，and the traditional interpolationmethods are not fitting well with the discrete data.This resourch，based on the regionalized variable and variation function of Kriging along with Inverse DistanceWeighted（IDW），put forward a new algorithm nesting the twomethods.Based on investigation in a largemolybdenum deposit at domestic，the conclusion is that this algorithm is simple and can greatly improve the fitting accuracy of the digital terrain model（DTM）of oxidation belt.

Oxidation belt，Kriging，IDW，DTM fitting

2013-08-04）

*国家自然科学基金项目（编号：51104010），教育部基本科研业务费项目（编号：FRF－SD－12－001A），国家高技术研究发展计划（863计划）项目（编号：2012AA062201）。

李 迪（1988—），女，硕士研究生，100083北京市海淀区学院路30号。