基于Hoek－Brown准则的数值模拟计算参数的研究

刘德峰王锐涛耿亚东刘 伟

（1.内蒙古科技大学矿业工程学院；2.河南永华能源有限公司）

基于Hoek－Brown准则的数值模拟计算参数的研究

刘德峰1王锐涛2耿亚东2刘 伟1

（1.内蒙古科技大学矿业工程学院；2.河南永华能源有限公司）

数值模拟中岩体力学参数的确定是非常重要的。详细介绍了M.Georgi法和Hoek－Brown法确定岩体力学参数的基本原理，以东升庙铅锌矿的岩体力学参数确定研究为例，以室内岩石试验为基础，测出岩块试件的物理力学参数，再综合考虑岩体节理裂隙的影响，并最终确定岩体力学参数。通过用FLAC3D数值模拟软件建立该矿的矿柱回收模型，进行地表沉降位移模拟，并对该矿区2号矿体的间柱和采空区顶板的3个位置的位移模拟曲线和同等位置的位移实测曲线分别进行比较，结果表明，通过Hoek－Brown法所确定的岩体力学参数较接近实际情况，可以作为该矿间柱回收模拟的基础数据。

Hoek－Brown法 M.Georgi法 数值模拟 岩体力学参数

在岩体的工程实践中，其中工程岩体力学参数的确定一直具有不确定性，是岩石力学最困难的研究课题之一。由于岩体的物理和力学性质在很大程度上受形成和改造岩体的各种地质作用过程所控制，往往表现出非均匀性、非连续性和各向异性等特征，使得岩体和岩石的力学性质产生了很大的差异［1］。确定岩体力学参数的最可靠的方法是进行大型原位试验，但是由于这种试验所需要的费用高、时间长和其他影响因素较多，所以，目前宏观岩体力学参数的确定比较困难，其发展受到一定限制。

本研究以东升庙铅锌矿为例，以室内岩石力学试验为基础，通过M.Georgi法和Hoek－Brown法将测得的岩石的抗拉和抗压强度、弹性模量、泊松比、以及岩石和岩体的波速与岩体的节理裂隙密度和岩体结构综合结合起来确定东升庙岩体力学参数。再运用FLAC3D［2-3］数值模拟方法将上面两种方法确定的岩体力学参数进行数值建模模拟2号矿体3个位置的沉降位移，并与IMS微震实测值相比较来确定该矿的岩体力学参数，并最终运用于工程实践。

1 岩体力学参数确定的方法原理

1.1 M.Georgi法原理［4］

M.Georgi方法是对大理岩、片麻岩、辉长岩、角山岩、玄武岩、流纹岩等15种坚硬岩浆岩和变质岩的岩石强度和岩体强度进行了研究后得出的经验方法。根据结构面的发育程度按下式对岩块内聚力Ck进行弱化，以获取含裂隙岩体的内聚力Cm：

式中，Cm为岩体的内聚力，MPa；Ck为岩块的内聚力，MPa，

σc为岩块试件的抗压强度，σt为岩块试件的抗拉强度；i为岩体的裂隙密度，条／m。

试验研究结果表明，室内岩块试件的强度与岩体强度之间有一定的关系，此关系可以近似地用岩体完整性系数［5］来表示。岩体完整性系数KV等于弹性波在岩体与岩石试件中的传播速度之比的平方，即

式中，Vpm为岩体中声波传播速度；Vpr为岩石试件中声波传播速度。

则岩体的抗压和抗拉强度、弹性模量、泊松比都是通过岩块试件的抗压和抗拉强度、弹性模量、泊松比与岩体完整系数的乘积来表示，其关系式为

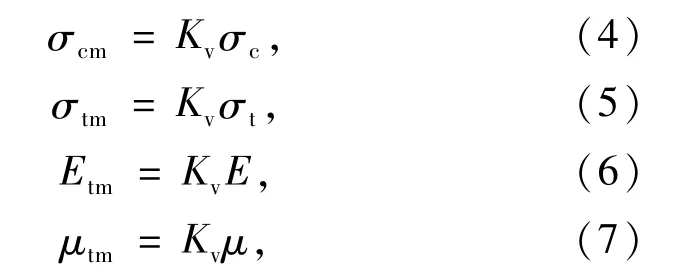
式中，σcm为岩体的抗压强度；σtm为岩体的抗拉强度；Em为岩体的弹性模量；E为岩块试件的弹性模量；μm为岩体的泊松比；μ为岩块试件的泊松比。

由库伦－摩尔准则［6］的几何图可知，岩石内聚力的增加或是减小基本上都不影响内摩擦角的变化，因此，岩体的内摩擦角可以近似地等于岩块试件的内摩擦角。

1.2 Hoek－Brown法原理［7］

1980年Hoek和Brown在分析Griffith理论的基础上，通过对三轴试验资料和现场岩体试验成果的统计分析，运用试验法推出了岩块试件和岩体极限主应力的关系为

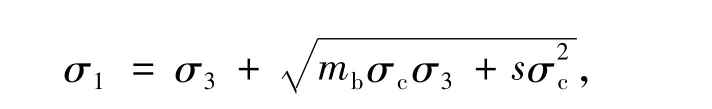
式中，σ1为最大主应力；σ3为最小主应力；mb、s为与岩性和结构面有关的参数，

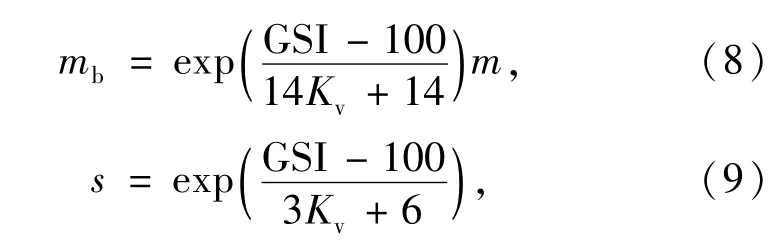
m为岩石的软硬强度，GSI为地质强度指标。

在求得mb，s后，即可利用Hoek－Brown准则提供的公式计算得出岩体力学参数。

（1）岩体抗压强度：

（2）岩体抗拉强度：

（3）岩体的弹性模量：

（4）岩体的抗剪力学参数：根据与Hoek－Brown准则相对应的Mohr－coulomb准则［5］，可求得岩体内聚力Cm和内摩擦角φ为

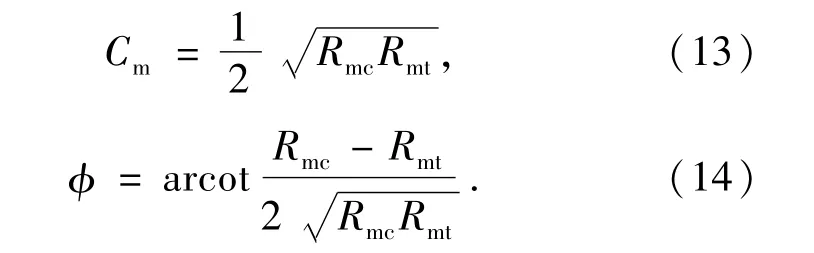
由上可知，为了利用Hoek－Brown准则来确定岩体的准强度性质，必须对岩体的3个参数做出评估：完整岩块试件的单轴抗压强度σc（可以根据室内试验测出）；完整岩块的Hoek－Brown常数m；岩体的地质强度指标GSI［8］（Z.T.Bieniawski［9］经过大量的试验研究认为，GSI在数值上具有和岩体质量RMR值相互等效的关系［10］）。

2 东升庙铅锌矿岩体力学参数的确定

2.1 岩石力学参数和岩体质量评价

通过对东升庙铅锌矿钻孔岩芯取样，在内蒙古科技大学室内岩石力学实验室对岩石进行了样品加工。根据要求，岩石物理力学性质试验需要做岩块密度试验、单轴压缩变形试验、单轴抗压强度试验、抗拉强度试验、岩石抗剪试验，超声波测波速试验等，所测得的岩块试件物理力学参数如表1所示。

通过对该矿的勘探线剖面图和岩体结构进行分析，并通过现场测量得岩体的节理裂隙密度和裂隙平均间距如表2所示。

表1 东升庙铅锌矿岩石物理力学参数

表2 东升庙铅锌矿岩体结构参数

通过对该矿的工程地质调查，根据岩块强度、RQD、节理间距、节理条件和地下水5类参数的实测资料，按照标准评分后相加得岩体质量总分RMR值，即GSI值。具体值如表3所示。

表3 东升庙铅锌矿岩体RMR评价结果

2.2 岩体力学参数的确定

2.2.1 M.Georgi法

以室内和室外测得的岩石物理力学参数为基础，由式（3）得出岩体的完整性系数，再由式（4）～式（7）计算得出岩体的抗压强度、抗拉强度、弹性模量和泊松比，再根据在东升庙铅锌矿现场测得的岩体裂隙密度和式（1）计算求出岩体抗剪强度参数，其计算得到的岩体力学参数结果如表4所示。

表4 岩体力学参数

2.2.2 Hoek－Brown法

根据工程地质分析出的该矿的各岩石类型的m值、与岩体质量RMR值近似等效的地质强度指标GSI值以及式（8）和（9），可求出相对应的mb和s值，再根据式（10）～式（12）可计算得到岩体的单轴抗压强度、单轴抗拉强度、弹性模量力学参数，最后根据式（13）和式（14）计算求出岩体抗剪强度参数，其计算结果如表5所示。

表5 岩体力学参数

3 FLAC3D数值模拟

3.1 计算模型的建立

采用三维有限差分法程序FLAC3D数值模拟软件来完成该矿的数值建模。本次数值模型的计算范围通过现有的经验结合现场实地调查研究最终确定选取，模型的高度为814 m，模型x方向为矿体的走向，长为1 300 m；模型y方向为垂直矿体走向的方向，倾向宽为620 m；模型的z方向为竖直方向。

模型采用的是莫尔－库伦本构模型。设置本模型的单元体数为76 000个，网格节点数为82 466个。初始几何模型主要选取FLAC3D网格库中的Brick和Wedge 2种基本网格建立，通过多种基本网格组合建立成复杂的三维实体模型，对模型中的基本网格群进行Group设置，并分配不同的颜色进行区分，矿体模型空间分布图如图1所示。

3.2 数值模拟计算结果

把用M.Georgi法和Hoek－Brown法所确定的岩体力学参数分别赋值到FLAC3D软件中进行数值模拟，得到相应的z方向位移云图如图2和图3所示。为了更好地比较这2种方法中哪种方法所确定的岩体力学参数更符合实际情况，选择对2号矿体的850 m中段的8号间柱和900 m中段上方的采空区和980 m顶板的沉降位移进行监测，具体位置分别是图中的3号、2号和1号监测点，其所对应的监测曲线都是从下到上分布。

图1 矿体模型空间分布图

图2 M.Georgi法z方向位移云图

图3 Hoek－Brown法z方向位移云图

4 IMS微震监测系统及对比分析

4.1 IMS微震监测系统

该矿山的微震监测系统定位精度已进行分析，震源定位精度能够满足矿山安全生产的要求。基于JDI5.0微震数据分析软件，将通过SURPAC软件建立的三维模型.str文件和监测到并处理过的的微震事件.evp文件导入到JDI中。

4.2 对比分析

监测点位移曲线与实测位移曲线对比见图4。

图4 监测位移曲线与实测位移曲线对比

比较可知，用Hoek－Brown法所确定的岩体力学参数模拟出的M1、M2和M33个位置的位移沉降曲线更与微震监测曲线S1、S2、S3相接近，其相对误差都控制在15%以内，对应矿业工程来说，这个误差是允许的［10］。因此，针对于该矿，用 Hoek－Brown法所确定的岩体力学参数更符合实际，数值模拟的结果更接近实际情况，能更好地为现场提供指导。

5 结 论

（1）以室内岩石试验为基础，分别测出岩块试件的单轴抗压和抗拉强度、弹性量和泊松比，又综合考虑岩体的完整性系数和岩体的裂隙密度的影响，运用M.Georgi法和Hoek－Brown准则分别对岩体力学参数的确定进行分析研究，计算得出了2组岩体力学参数。

（2）运用FLAC3D数值模拟软件先对该铅锌矿进行建模模拟，然后把2种方法所计算的岩体力学参数赋值到软件中进行位移沉降模拟，选2号矿体的3个主要位置的模拟位移曲线与IMS微震监测曲线进行比较，经分析可知，随着深度的增加，z方向位移值不断减小，这是符合自然规律的，但是只有M曲线和S曲线相接近，所以通过Hoek－Brown法所确定的岩体力学参数才可以作为该矿矿柱回收模拟的基础数据，能够保证FLAC数值模拟更好地为矿山服务，指导矿山的安全生产。

［1］沈明荣.岩体力学［M］.上海：同济大学出版社，1999.

［2］陈育民，徐鼎平.FLAC／FLAC3D基础与工程实例［M］.北京：中国水利水电出版社，2008.

［3］彭文斌.FLAC3D实用教程［M］.北京：机械工业出版社，2009.

［4］朱旭波.地下金属矿岩体质量评价与采场结构参数优化研究［D］.长沙：中南大学，2012.

［5］于润沧.采矿工程师手册［M］.北京：冶金工业出版社，2009.

［6］张金团，杨学堂，易 武.Hoek－Brown准则m及s参数的确定方法［J］.山西建筑，2007（26）：30-31.

［7］谭文辉，周汝弟，王 鹏.岩体宏观力学参数取值的GSI和广义的Hoek－Brown法［J］.有色金属：矿山部分，2002（4）：16-18.

［8］郭延辉，侯克鹏，杨 泽.深部开采模拟中岩体力学参数的取值研究［J］.矿冶，2011（3）：7-12.

［9］王树仁，周洪彬，武崇福，等.采用综合评判方法确定工程岩体力学参数研究［J］.岩土力学，2007（10）：202-206

［10］韩现民，李 晓，成国文.基于RMR的节理岩体力学参数快速评价［J］.矿业研究与开发，2009（4）：13-15.

Study on Calculation Parameters of Numerical Simulation Based on the Hoek Brown Principle

Liu Defeng1Wang Ruitao2Geng Yadong2Liu Wei1
（1.College of Mining Engineering，Inner Mongolia University of Science and Technology；2.Henan Yonghua Energy Co.，Ltd.）

It is important to determine rock massmechanics parameters in numerical simulation.The basic principles of M.Georgimethod and Hoek Brownmethod of determining themechanical parameters of rock mass are introduced in detail.Taking research on determining rockmassmechanical parameters in Dongshengmiao Lead-zinc Mine as an example，and based on the physical andmechanical parameters of rocks at indoor laboratory tests，the effectof rock joints and fissureswas considered to eventually determine rockmechanics parameters.The recoverymodel of the ore pillarwas builtby FLAC3Dnumerical simulation software，to simulate the surface displacement settlement.Then，the simulation displacement curve of three positions at columns and goaf roofs of No.2 ore body were compared with themeasured displacement curve at the same place.The comparison results showed that the rock mechanics parameters determined by Hoek-Brown method were closer to the actual situation，which can be used as the basic data for simulating the recovery of rib pillars.

Hoek-Brown method，M.Georgimethod，Numerical simulation，Mechanical parameters of rock mass

2013-08-07）

刘德峰（1988—），男，硕士研究生，014010内蒙古包头市昆区阿尔丁大街7号。