螺杆钻具传动轴的疲劳寿命预测及改进设计*

刘 慷，李 健

(广西科技大学机械工程学院，广西柳州 545006)

螺杆钻具传动轴的疲劳寿命预测及改进设计*

刘 慷，李 健

(广西科技大学机械工程学院，广西柳州 545006)

利用有限元法，建立某厂螺杆钻具传动轴的力学模型，从静力学及疲劳两个方面对其性能进行分析。并通过ANSYS Workbench软件分析确定传动轴可能存在危险点的Von Mises应力值。从生产实际出发，提出了两种改进的方案。利用局部应变法中修正后的史密斯公式对传动轴进行寿命预测，为传动轴的设计提供了理论依据。

螺杆钻具;传动轴;ANSYS;疲劳;史密斯公式

1 引言

随着钻井技术的不断发展与完善，新型技术的出现与革新层出不穷［1］。而动力钻具的使用寿命直接影响到钻井速度以及钻井工艺的发展。螺杆钻具作为钻井工程中的常用钻具之一，其寿命及性能的良好显得越为重要。而传动轴总成作为螺杆钻具实现钻井作业的纽带，其本身的疲劳寿命成为影响钻具质量的重要指标之一。据统计，80%的钻具失效都与疲劳有关，其中，机械载荷造成的疲劳事故比比皆是。因此，传动轴的损坏与失效愈来愈被设计人员所关注。某些学者，针对万向轴的力学特性进行分析，采用ANSYS软件并用雨流法对钻具寿命进行评测［2］;某些学者，分析了螺杆钻具组合的的受力状态，建立了适用于上弯式螺杆钻具组合和下弯式螺杆钻具组合的二维以及三维小挠度静力学分析的力学模型和数学模型［3］;某些学者，针对螺杆钻具传动轴的失效问题，建立了螺杆钻具传动轴的失效树模型，为研究失效提供了便利［4］。

快速、有效、低成本地实现钻具传动轴的结构改进，提高传动轴的疲劳寿命，缩短钻具产品的开发与制造周期，提高预测钻具疲劳寿命的准确性十分重要。应用有限元法进行分析，可对钻探机具应用中出现的各种问题进行力学上的理论分析和工程数值模拟［5］。笔者针对这些问题，对某厂生产的螺杆钻具传动轴建立有限元模型，通过ANSYS Workbench软件，对传动轴可能存在的危险截面进行分析，提出了两种改进的方案并进行有限元分析，将改进后的分析结果与原结果进行对比。最后使用修正的史密斯公式对传动轴的疲劳寿命进行预测，其结果可作为相关产品设计过程中的参考与理论依据。

2 传动轴的静力学分析

2.1 传动轴受力情况

传动轴的作用是将马达的旋转动力传递给钻头，同时承受钻压所产生的轴向和径向负荷。其承受的载荷主要有转子轴向力G［6］;传动轴活塞力Pd;转子、万向轴、传动轴和钻头重力的轴向分量Wcos;钻压Pb;扭矩M及侧向力Pa;通过研究发现，在常用工作范围内，扭矩对传动轴的影响较大，而实际工况中扭矩更容易得到。

2.2 建立传动轴有限元模型

某厂生产的传动轴材料为40CrMnMo，为优质调质钢，根据厂家所提供的图纸，利用Workbench平台的DM模块，在Ansys Workbench软件中建立传动轴模型。采用十节点线性应变四面体单元，对建好的模型进行网格划分。其有限元模型如图1所示。

2.3 分析模型并计算结果

传动轴材料40CrMnMo，传动轴外径203 mm，弹性模量取206 GPa，泊松比0.3，密度取7 870 kg/m3。螺杆钻具的主轴转矩M是影响钻头机械钻速的主要因素［7］。根据厂家提供的技术资料，本文所研究的传动轴的工作扭矩为7 580 N·m，最大扭矩为11 800 N·m，为保证传动轴可以安全工作，采用最大扭矩11 800 N·m为载荷条件，即大头面固定，小头螺纹面加载11 800 N·m的扭矩。对传动轴进行静力学分析，其结果如图2所示。

图1 传动轴有限元模型

图2 传动轴整体应力云图

通过ANSYS系统可将传动轴受到外载与约束作用状态下的应力分布计算出来。由分析结果可知，传动轴最大应力为131.61 MPa，位于传动轴与水帽相连接的螺纹根部。而小径部分也受到较大应力，为117 MPa。通过厂家的反馈，传动轴也常在此处失效。而传动轴的最大位移出现在小径靠近水帽处，最大变形为0.544 mm。传动轴的位移分布如图3所示。

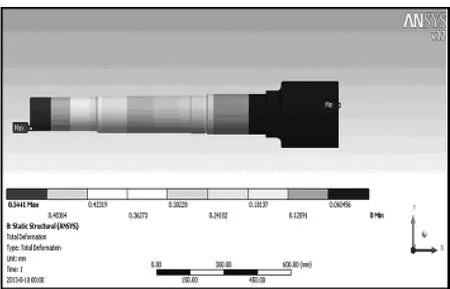
图3 传动轴的位移云图

3 传动轴的疲劳预测

3.1 局部应变法中的史密斯公式

螺杆钻具的失效是一个持续的、逐步积累的过

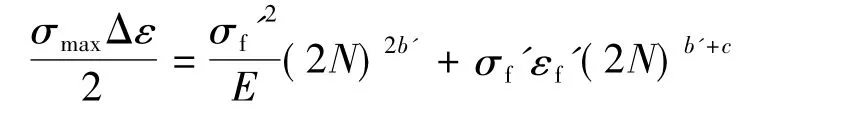
式中:σmax为最大应力值;Δε为局部应变幅值;σf'为疲劳强度系数;εf'为疲劳延性系数;E为材料的弹性模量;N为疲劳寿命;c为疲劳延性指数;b'为考虑了零件的表面加工与尺寸影响后的疲劳强度指数。

3.2 传动轴的疲劳寿命预测与解算程序

断裂与疲劳在钻具事故中占的比例较大，危害也较严重［9］。通过的修正的史密斯公式的化简，得到疲劳寿命N的解算式。化简过程如下:程［8］。螺杆钻具每旋转一圈都会产生一次应力，应力集中的管体或接头会逐渐形成微裂纹，最终导致其失效。

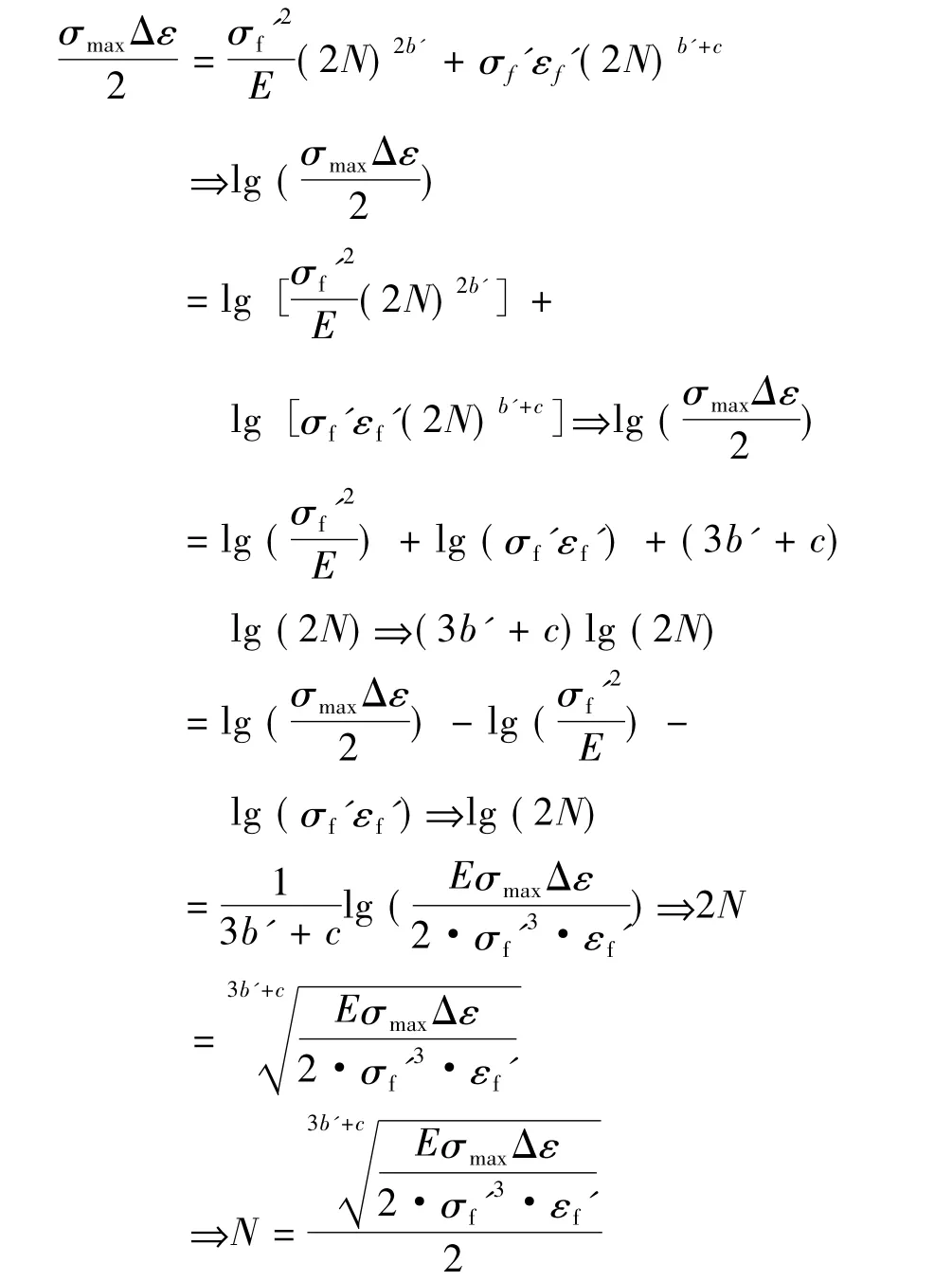
零件的疲劳破坏都是从应变集中部位的最大局部应变处首先开始，并且在裂纹萌生以前，都要产生一定的塑性变形;而局部塑性变形是疲劳裂纹萌生和扩展的先决条件。因此，决定零件疲劳寿命的是应变集中处的最大局部应变。本文通过修正后的史密斯公式，考虑了零件的表面加工与尺寸等因素对高周疲劳的影响。修正后的史密斯公式为:

考虑到公式中存在开n次方根的根，同时需多次进行对数求解，且需代入的参数非常多，因此本文通过Visual Basic语言编程环境，将以上的计算程序化，并作可视化窗口。将有限元分析的结果输入程序中，其解算结果如图4所示。由此可得，传动轴的疲劳寿命近似为1.2×106次。

为方便计算，将计算结果程序可视化，得到材料的S－N曲线如图5所示。通过查阅资料，得到材料40CrMnMo中a=23.9545，b=－6.8775。

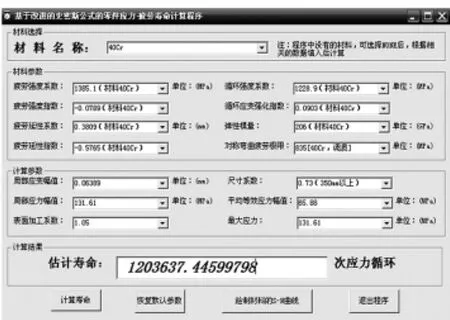
图4 史密斯公式计算结果

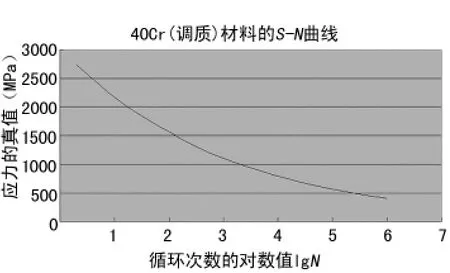
图5 S－N曲线图

由S－N曲线所示，材料曲线无限趋近于1×106次方，这与之前所得出的传动轴疲劳寿命约为1.2×106次的结果基本一致。

4 传动轴的改进方案

4.1 两种改进方案

本文对传动轴的改进与设计，是以减小应力，提高疲劳寿命，提高产品可靠性为目的。

第一个方案是在保证基本尺寸不变的基础上，缩短传动轴小径部分长度20 mm;第二个方案是保证原有尺寸基本不变的前提下，为有效抵抗外界磨损，将传动轴小径部分直径增加5 mm。其他条件不变。分别将改进好的模型进行有限元分析，其分析结果对比如表1所列。

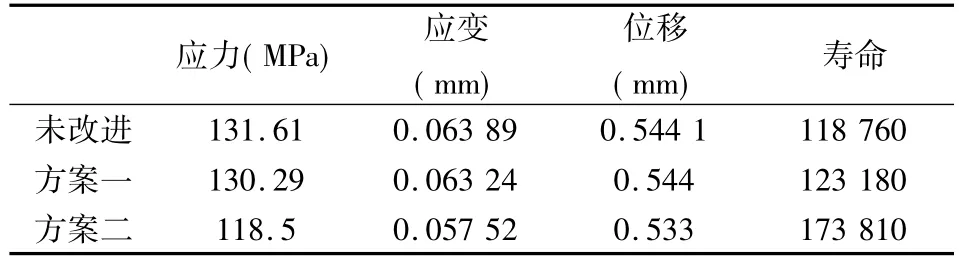
表1 传动轴分析结果

第一次改进后的传动轴，其危险截面处应力值有略微下降，为130.20 MPa;应变减小为0.06324 mm;其疲劳寿命提高至1.23×105次;而位移与改进前的传动轴位移变化值相比较并无明显变化。虽然第一次改进的传动轴在应力及寿命上有一定改善，但总体性能改善不高。而第二次改进的传动轴，危险截面处应力下降明显，为118.5 MPa;危险截面处应变降低为0.057 52 mm;最大变形位移减小为0.533 mm;传动轴的疲劳寿命提高为1.73×105次。通过对比，第二方案的改进，在增加传动轴刚度的同时，不仅有效的降低传动轴各部位的应力与变形情况，而且显著提高了传动轴的使用寿命，改善了传动轴的可靠性。说明此改进方法具有一定的有效性与可行性。

5 结论

螺杆钻具传动轴的失效主要在其结构设计与复杂的工作环境等因素的共同作用。CAE技术与疲劳理论相互验证，发现传动轴小径直径对其刚度及寿命都有着明显影响，从而说明有限元法对螺杆钻具传动轴的设计与优化有着一定的指导意义。

［1］ 王俊涛，谭春飞，王莉萍，等.螺杆钻具传动轴失效分析与提高寿命措施探讨［J］.西部探矿工程，2010(5):57－60.

［2］ 高晓刚.螺杆钻具万向轴力学特性分析及寿命预测［D］.西安:西安石油大学，2009.

［3］ 王胜利.煤矿工程孔中螺杆钻具组合力学特性分析及应用［D］.北京:煤炭科学研究总院，2005.

［4］ 何文涛，螺杆钻具失效分析［D］.西安:西安石油大学，2008.

［5］ 詹 军，殷 琨，于清杨.钻探机具的有限元分析［J］.吉林大学学报，2002(2):203－204.

［6］ 祝效华，童 华，赵红超，等.螺杆钻具传动轴力学特性评价［J］.石油钻探技术，2007(1):56－59.

［7］ 万朝晖.螺杆钻具的工作特性和结构参数的分析研究［J］.石油机械，2001，29(10):25－27.

［8］ 王 俊.螺杆钻具的静态及动态分析［D］.沈阳:沈阳工业大学，2013.

［9］ 毕雪亮，王长江，闫 铁，等.深井钻具失效分析与预防［J］.钻采工艺，2005(6):27－31.

Fatigue Life Prediction and Improved Design for Drive Shaft in Positive Displacement Motor

LIU Kang，LI Jian
(Academy of Mechanical Engineering，Guangχi University of Science and Technology，Liuzhou Guangχi 545006，China)

In the paper，the mechanical model of drive shaft is established by finite element method，which is analyzed from two aspects of static and fatigue.Through the ANSYS software，the dangerous point of von Mises stress value is defined.Two improved schemes are presented by actual production.Using the revised Smith formula of local strain method to predict the fatigue life and a theoretical basis is provided for the design of transmission shaft.

PDM;drive shaft;ANSYS;fatigue;smith formula

P634.3;TE921

A

1007－4414(2013)05－0068－03

2013－08－29

刘 慷(1988－)，男，陕西宝鸡人，硕士研究生，主要从事机械设计及理论方面的研究。