大学生数学史教育现状的灰色模糊评价模型

徐 婷

(海南师范大学数学与统计学院，海南海口571158)

引 言

数学史是研究数学的发生、发展过程及其规律的一门学科，它的研究主要对象是历史上的数学成果和影响数学发展的各种因素，探索前人的数学思想，借以指导数学的发展，并预测数学的未来。法国著名数学家庞加莱说过:“如果我们要预见数学的未来，适当的途径就是研究这门科学的历史和现状。”这句话深刻揭示了数学史在数学发展中的重要作用。我国著名数学家吴文俊说过:“假如你对数学史的历史发展，对一个领域的发生和发展、兴旺和衰落，对一个概念的来龙去脉，对一种重要思想的产生和影响等许多因素都弄清楚了，我想就会对数学了解得多，对数学的现状就会知道的更清楚、更深刻，还可以对数学的未来起一种指导作用”［1］。这些都说明数学家很早就意识到数学史的重要性。《普通高中数学课程标准(实验稿)》在2003年4月正式颁布，新课标明确指出:“数学是人类文化的重要组成部分。数学课程应适当反映数学的历史、应用和发展趋势，设立‘数学史选讲’等专题”［2］。这充分体现了对课改中数学史在数学教育中的作用和价值的重视［3］。

但是现在很多学生对数学缺乏兴趣，甚至讨厌数学。经常听到学生说数学课很难很烦，考试总不及格，上数学课还不如睡觉等等。此为本文研究的现实背景。本文通过调查研究，试图从学生对数学史的认识、了解、运用能力这三方面了解师范类大学生对数学史教育的认识现状。我们把学生掌握数学史的情况分为优秀、良好、一般、不合格四个等级，首先设定不同等级的分数区间，其次通过对问卷调查进行打分，确定学生所属等级，最后根据各个等级人数多少、优秀率、不合格率来评判数学史教育现状好坏。

本文主要采用灰色聚类分析与模糊聚类分析方法来研究。

一 数学模型理论

(一)灰色聚类分析

灰色聚类分析是由华中科技大学邓聚龙教授提出的一种定量评价方法，是建立在灰数的白化函数基础上，将评价对象对不同评价指标所拥有的白化值，按若干个灰色进行归纳整理，从而判断聚类对象属于哪一种灰类的方法(即先聚类后排序)。灰数是指在某一个区间或某一个一般的数集内取值不确定的数。白化权函数是指在直角坐标系中的一条三折线或s型曲线，它可以定量地描述某一评估对象隶属于某个灰类的程度(即随着被评估指标或样点值的大小而变化的关系)。主要步骤为:1.构建灰色聚类样本;2.确定灰类白化权函数;3.求聚类权;4.求聚类系数;5.构造聚类向量，进行聚类。

(二)模糊聚类分析

模糊聚类分析即用模糊数学的方法来进行聚类分析;研究不同对象间的关系，表达了样本类属的中介性，更能客观反映要研究的问题，是一种软划分。具体步骤为:1.建立模糊相似关系并将数据标准化;2.构造模糊相似矩阵;3.选取适当的置信水平值进行聚类。

二 实证分析

(一)聚类指标体系

本文调查大学生数学史教育现状，以海南师范大学数学专业学生为个案研究。在参照大量数学史研究文献、论文及专家建议基础上，主要从学生对数学史的认识、了解、运用能力这三方面考察并设计问卷，建立数学史教育现状评价指标体系结构。具体是:

一级指标:数学史教育现状A

二级指标:对数学史的认识B1

(C1积极的情感、C2科学的态度、C3正确的世界观、C4获得的途径)

了解的数学史知识B2

(C5数学家、C6数学重要事件、C7数学原理、C8概念起源)

运用数学史的能力B3

(C9学习能力、C10应变能力、C11创新能力)

(二)灰色聚类分析

1.构建灰色聚类样本

采用问卷调查方法得到580份数据，其中总分在80分以上有79人，70－80分121人，60－70分98人，60分以下282人。而灰色聚类研究的是小样本事件，所以根据问卷情况采用分层抽样方法按1:20抽取4、6、5、14共29份问卷数据。根据上述指标体系里问卷的设定再对三个指标采用1～10分制分别打分，分值越高，说明其素质越高。将每个学生的得分取平均值(这29份问卷对应的29个学生就是本文的聚类对象)。

聚类对象 X={X1，X2，……，X29}有 29 个，每个对象有3个聚类指标Y={B1，B2，B3}，每个指标按评估标准分为4个等级(优秀、良好、一般、不合格)，那么第i个对象(i=1…29)对第j个聚类指标(j=1，2，3)的样本值记为Xij(即聚类白化数如表1所示)，将第i个对象归入第k(k∈{1，2，3，4})个灰类中(如表2所示)，称为灰色聚类

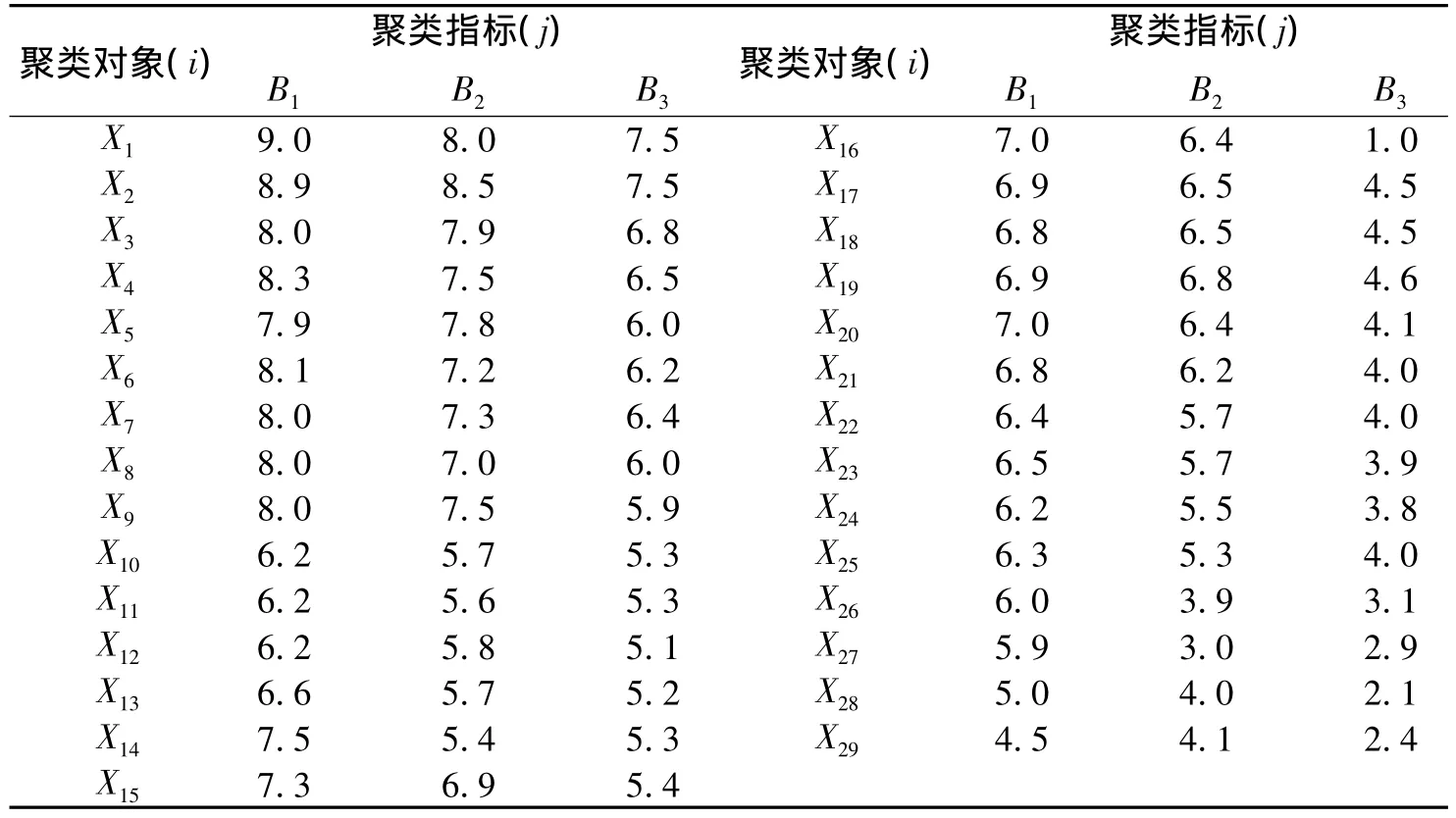
表1 聚类对象及聚类白化数Table 1 the clustering object and clustering albino Xij

在专家建议基础上素质评价采用4个评价灰类(k)，如表2所示。

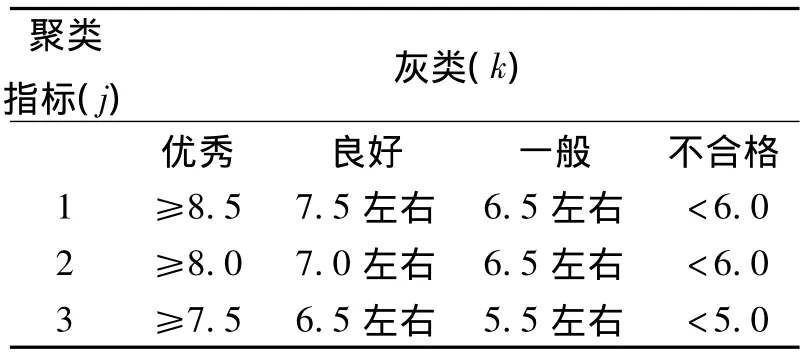
表2 聚类分级标准Table2 cluster grading standards

2.确定灰类白化权函数［6］

将n个对象关于指标j的取值相应的分为s个灰类，其中j指标k子类的白化权函数记为(.)一个典型的白化权函数为起点、终点确定的左升、右降连续函数。白化权函数还有三种常见形式，分别为上限测度白化权函数、适中测度白化权函数和下限测度白化权函数，记为(a1，b1，－ ，a2)，(a1，b1，－ ，－ )，(－ ，－ ，b2，a2)，如图1(a)～(d)所示。

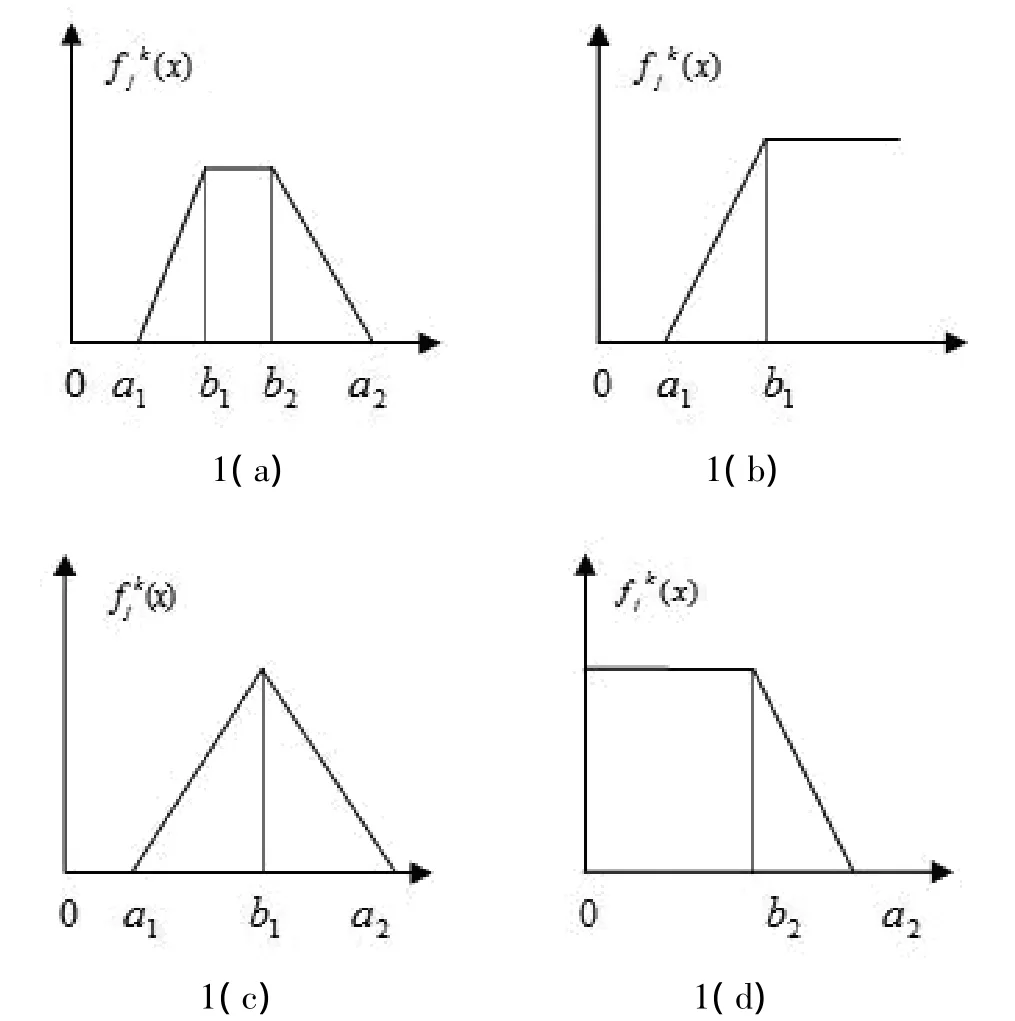
图1 白化权函数Chart 1 whitening weight function

根据表2，对数学史的认识、了解的数学史和运用数学史的能力各指标关于各灰类的白化权函数分别设为:

表3 计算结果Table 3 the results

3.求聚类权

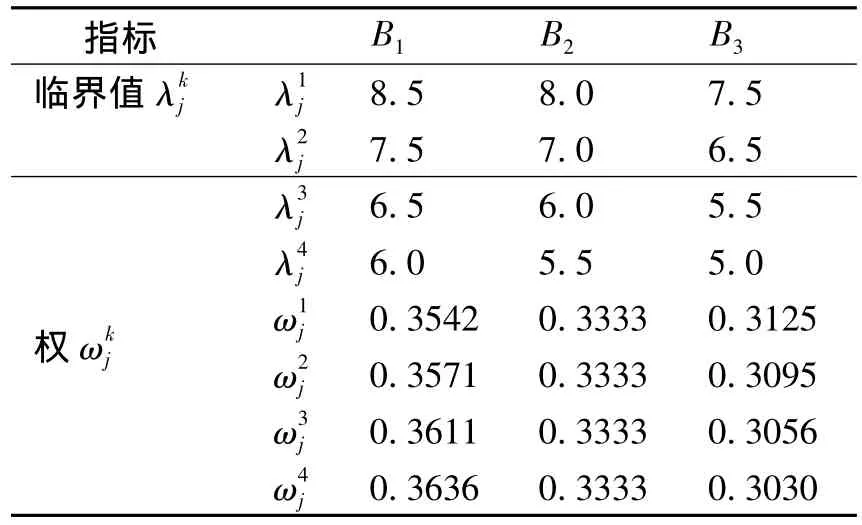
表4 临界值及聚类权值Table 4 Threshold and cluster weights

4.求聚类系数

聚类系数揭示了第i个聚类对象属于第k个灰类的程度。表示为根据公式，当 i=3 时(8.0)×0.3542+(7.9)×0.3333+(5.8)×0.3125=0.5708同理可得:=0.4285=0=0

5.构造聚类向量，进行聚类

当 i=3 时，向量 σ3=(0.5708，0.4285，0，0)，其中，max{}==0.708，说明该对象属于第一灰类，即该学生数学史教育现状问卷结果为优秀。同样可得到其他对象的聚类结果，如表5所示。

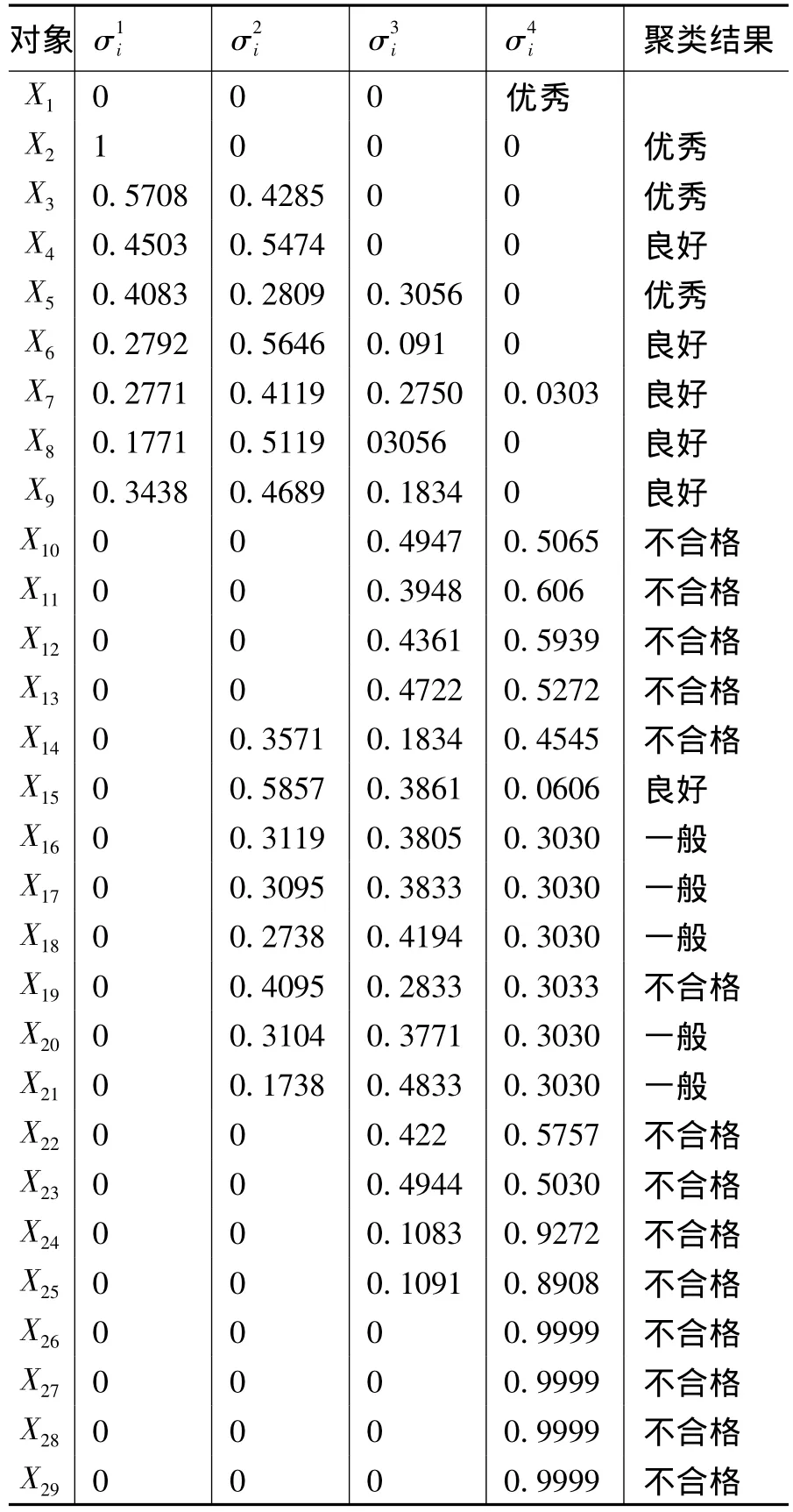
表5 聚类系数及分析结果Table 5 clustering coefficients and analysis results

上述结果表明29个对象中有4个优秀，6个良好，5个一般，14个不合格。优秀率仅达到13.8%，不合格率占将近一半，说明数学史教育现状不容乐观。

(三)模糊聚类分析

1.建立模糊相似关系并将数据标准化

由灰色聚类办法得到的29个聚类行向量组成的29×29矩阵比较大，所以从上述29个行向量中抽取 10 个行向量(X1、X2、X6、X7、X16、X17、X23、X24、X25、X26)优秀、良好、一般各两个，不合格四个组成原始数据矩阵σ，其中σ的行指标为聚类对象，列指标为灰类指标，矩阵形式如下:

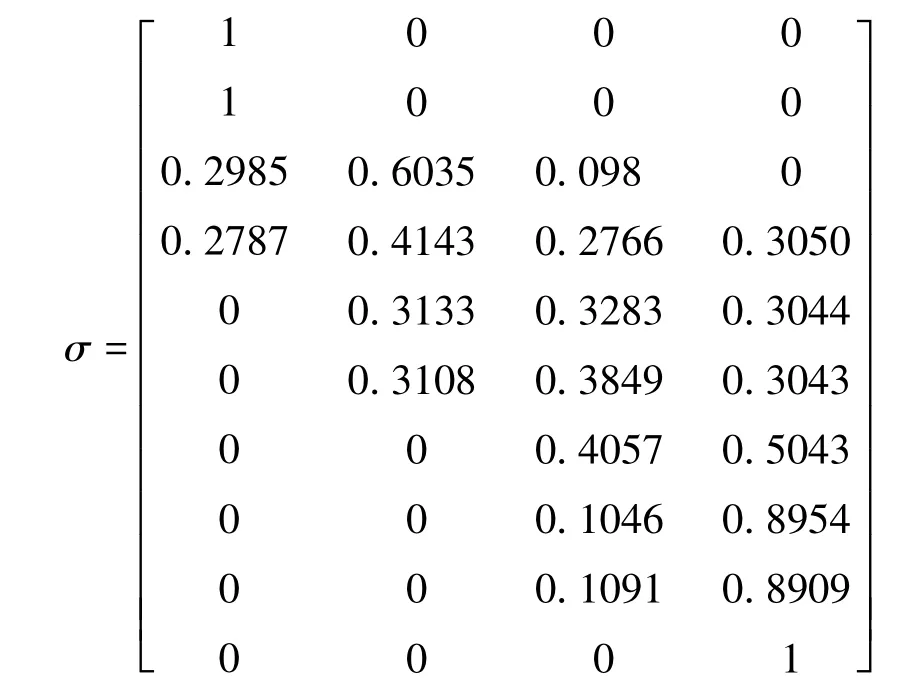
2.构造模糊相似矩阵

相似系数，rij=R(σi，σj)，rij建立模糊相似矩阵:

3.选取聚类

利用直接聚类法，取不同λ求相似类，最后获得λ不同水平上的等价分类。其动态聚类图如图2所示。

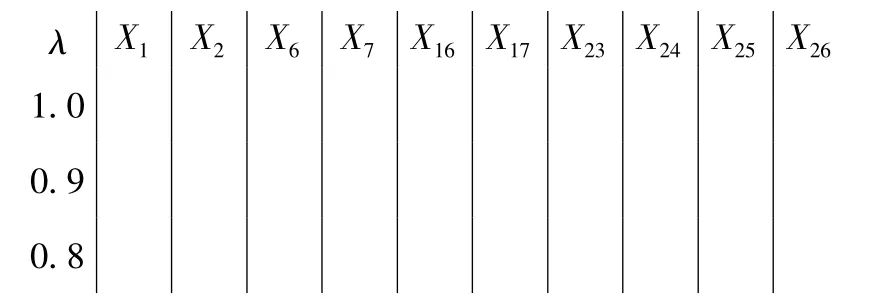
图2 动态聚类图Chart 2 Dynamic clustering chart

三 分析与评价

由表5的行方向知:

聚类对象X1、X3属于第1灰类，问卷评价为优秀。、X4、X6属于第2灰类，评价为良好。X16、X18属于第3灰类，评价结果为一般。其他为第4灰类。即有4个优秀，5个良好，6个一般，14个不合格。优秀率仅达到13.8%，不合格率占将近一半，学生对数学史的认识、了解的数学史知识以及运用数学史能力会影响学生的学习情况。也说明数学史教育现状不容乐观，不管是学校还是教师、学生都要加大重视力度。

由列方向知:

总体来说:学生对数学史的认识比较高，都能认识到数学史的重要性;但掌握的数学史知识并不是很好，主动获取这方面知识的意向不够;学生运用数学史的能力非常差。

由图2知，当λ=0.9时，所有对象的聚类可划分为 7 个类别，{X1、X2}、{X6}、{X7}、{X16、X17}、X23、{X24、X25}、{X26}。

当λ=0.8时，对象可划分为4个类别。{X1、X2}、{X6、X7}、{X16、X17}、{X23、X24、X25、X26}与之前灰色聚类得到的结果是一致的。由于所有对象各自成类或全部对象并入一类没有实际意义，所以置信水平取0.8比较合适，说明两种聚类方法可行。

结 语

本文采用灰色和模糊聚类方法建立评价模型，结合实例予以说明。该模型计算过程简单，充分利用了各种灰类程度的评价信息，评价结果可靠。从总体上看，评价结果能较客观反应实际情况，方法科学合理［10］。

从数据结果分析得知，超过80%的学生已经认识到数学史的重要性，但却很少有人花时间去研究、学习，掌握的数学史知识比较差，运用数学史能力更差。为使数学史教学不停留在表层，真正对我们的学习、生活、精神有帮助，要先从教师、学校做起。就此提出一些建议与措施:1.大学教师在上数学专业课时能从相关数学史讲起;2.提高选修课质量，延长选修课时间，考虑选修课转化为必修课，分四年教授;3.形成良好的数学史学习氛围，多举办数学史讲座、数学史趣味演讲等，调动师生的积极性。

［1］21世纪中国数学教育展望课题组.21世纪中国数学教育展望(第一辑)［M］.北京:北京师范大学出版社，1993.

［2］王森.美国“数学史在数学教学中的应用”专题会议介绍［J］.数学通报.1999(8).

［3］王秀琴.当前高中数学教学中应用数学史知识的调查研究［D］.济南:山东师范大学硕士毕业论文，2011.

［4］吴文俊.在教育部的全国高校中外数学史讲习班开学典礼上的讲话［A］.中国数学史论文集(二)［C］.济南:山东教育出版社，1986.

［5］中华人民共和国教育部.普通高中数学课程标准(实验)［M］.北京:人民教育出版社，2003.

［6］吴顺祥.灰色粗糙集模型及其应用［M］.北京:北京科学出版社，2009.

［7］谢季坚，刘承平.模糊数学方法及其应用·第3版［M］.武汉:华中科技大学出版社，2006.

［8］刘思峰，郭天榜，党耀国等.灰色系统理论及其应用［M］.北京:科学出版社，1999.

［9］陈水利，李敬功，王向公.模糊集理论及应用［M］.北京:科学出版社，2005.

［10］金玲玲，汪文俊，王喜凤.大学生综合素质的灰色模糊聚类评价模型［J］.计算机技术与发展，2012(5).