卫星钟差的仿真研究

杨 健，张 驰

(海军驻南京地区航天机电系统军事代表室，南京 210006)

0 引言

卫星导航仿真系统是卫星导航系统建设过程中一个不可或缺的部分。在导航卫星星座布设完成前，利用卫星导航仿真系统可以完成对地面运控系统和用户接收机的相关测试。为此，卫星导航仿真系统需要提供包括卫星钟差在内的各种仿真测试数据。

在卫星导航定位系统中，卫星钟差作为观测数据的主要误差源之一，其精度直接影响着定位系统的精度和性能［1］。高逼真度的卫星钟差模型可以实际地反映系统运行状况，在卫星导航仿真系统中起着重要作用。

卫星钟差，即卫星钟读数T与系统时间t 之间的差值，可以用一个二次多项式表示:

其中a0、a1和a2分别是t0时刻卫星钟相对于系统时间t的钟差、钟速和钟漂，△T 代表卫星钟的钟差噪声。

在以往的卫星钟差仿真中，没有考虑钟差噪声△T，或是简单地用白噪声代替。实际上，卫星钟差噪声主要由5 种独立的随机噪声组成，包括随机游走调频噪声(RWF）、闪烁调频噪声(FF）、白色调频噪声(WF）、闪烁调相噪声(FP）和白色调相噪声(WP）。不同种类卫星钟的噪声构成不同，同一种类卫星钟的噪声特征也不完全相同，而且随着取样时间的变化，卫星钟差噪声会表现出不同的特性。在高逼真度的卫星导航仿真系统中，更需要真实体现卫星钟差的噪声特性。

黄观文等［2］用估计随机噪声类型的卡尔曼滤波进行在轨卫星钟差估计与预报精度分析，定量揭示了不同类型星载卫星钟间的精度差异。王潜心等［3］使用附加了周期项和随机项的线性模型，进行卫星钟差仿真，精度最高可达0.3 ns，但要实时处理大量的观测数据，工作量很大。而在国外的一些仿真平台中，也将随机噪声加入软件中，像Satnav、NAVSIM 等。但是，这些软件也只是简单地用白噪声处理［4］。

本文从修正Allan方差的角度，分析不同卫星钟的噪声特性，结合上文提到的5 种独立的随机噪声模型和二次多项式模型，进行拟合仿真，得到高逼真度的卫星钟差仿真模型。

1 卫星钟差的噪声特性分析

由于卫星钟差包含5 种随机噪声，而这些噪声不满足平稳遍历的条件，其标准方差是发散的，因此需要用修正Allan方差来表征卫星钟差的稳定度特性。

修正Allan方差的定义［5］为

其中，＜·＞表示时间平均，y(t）和x(t）表示卫星钟差的频域值和时域值，τ0为时间间隔，n为取样个数，τ=nτ0为取样间隔，N为取样间隔为τ0时总的采样数目。图1 给出了5 种随机噪声的修正Allan方差值。

接下来，使用修正Allan方差对实际卫星钟差数据进行稳定度的评估。使用的数据是来自IGS 网站的钟差数据(2011年6 月20 日），其采样间隔为30s。从中采集了PRN2、PRN3、PRN9、PRN11 卫星钟的钟差数据，其中PRN2和PRN11 是铷(Rb）钟，PRN3和PRN9是铯(CS）钟。计算采集到的钟差数据的修正Allan方差，得到的结果如图2所示。

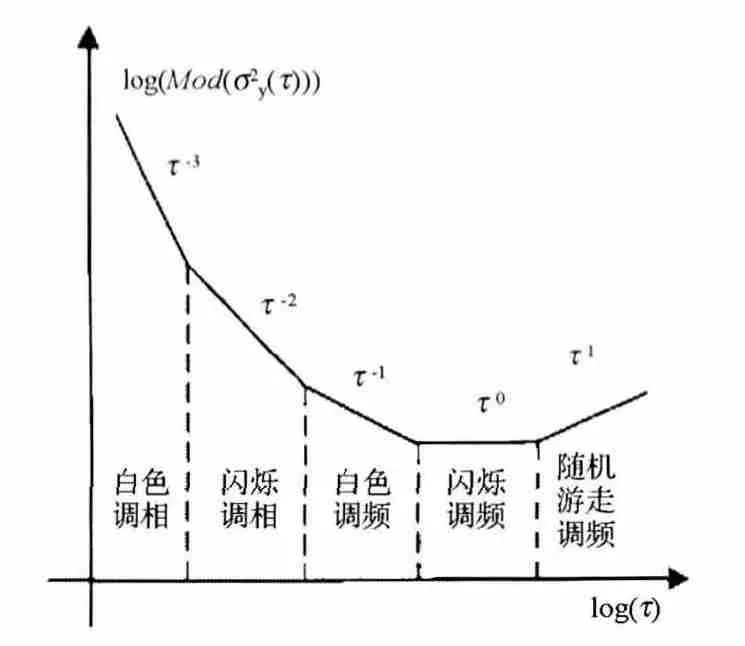
图1 5 种随机噪声的修正Allan方差

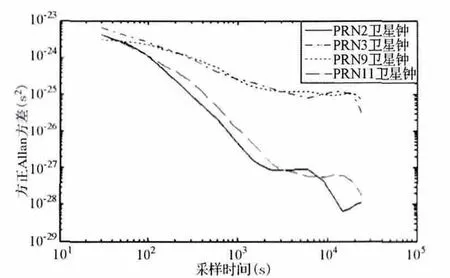
图2 各卫星钟的修正Allan方差值

对比图1中5 种随机噪声的修正Allan方差，可以得出以下结论:

1）对于铯钟来说，当采样点在30～3000 s 范围内时，主要表现为白色调频噪声(WF），大于3000 s时则是由多种噪声组合构成;

陶氏全球压敏工业业务主管、大中华区市场经理霍肖捷表示：“作为压敏行业的领先企业，我们提供创新的有机硅压敏胶和离型剂解决方案，满足本地客户特有诉求和本地市场需求。陶氏卓越的产品助客户赢得宝贵的竞争优势，从而在竞争激烈并不断变化的电子显示行业立于不败之地。”

2）对于铷钟来说，当采样点在30～100 s 范围内时，主要表现为白色调频噪声(WF），随着采样时间的增加，变成以闪烁调相噪声(FP）为主，而在大于3000 s 以后也是由多种噪声组合构成;

3）在本段采样时间范围内，铷钟的修正Allan方差值要小于铯钟，频域稳定度要较好于铯钟;

然后，对实际钟差数据进行二次多项式拟合，从而得到钟差拟合数据，实际钟差数据与拟合数据的差值即为钟差噪声数据。得到的拟合参数如表1所示，钟差噪声数据如图3所示。

表1 二次多项式拟合参数

计算钟差噪声数据的修正Allan方差，得到结果如图4所示。与原钟差数据的修正Allan 值进行对比，可以看出，图2与图4的结果完成一致，钟差噪声数据完整保留了原钟差数据的频域稳定度特性。后续进行的钟差噪声仿真，其主要目标就是仿真出与实际钟差噪声数据在修正Allan方差值上具有一致性的仿真噪声数据。

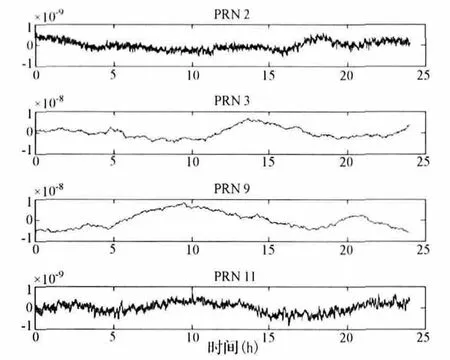
图3 各卫星钟的钟差噪声值

图4 各卫星钟的钟差噪声修正Allan方差值

2 卫星钟差的仿真方法

由于随机游走调频噪声、闪烁调频噪声、白色调频噪声、闪烁调相噪声和白色调相噪声这5 种噪声是相互独立的，因此钟差噪声的修正Allan方差可以看成是这5 种噪声的修正Allan方差值的加权和［6］，即

图5 仿真钟差噪声的具体流程图

(1）通过下述方法得到5 种随机噪声的仿真值，其中yi表示每种随机噪声的频域值:

图6 5 种随机噪声仿真数据的修正Allan方差值

表2 仿真噪声的拟合参数

从表2 可以看出:

(1）铷钟(PRN2和PRN11）的拟合参数中RFP的值较大，说明闪烁调相噪声(FP）占主导地位;铯钟(PRN3和PRN9）的拟合参数中RWF的值较大，说明白色调频噪声(WF）占主导地位。这点与上文图2.2 得到的不同钟的钟差噪声特性相一致，说明得到的拟合参数是符合实际特性的。

(2）在短期的钟差仿真中，随机游走调频噪声(RWF）作用不明显，此次仿真中RRWF为0。

使用表2中的拟合参数，分别对PRN2、PRN3、PRN9、PRN11 这四个卫星钟的钟差噪声进行仿真，计算仿真结果的修正Allan 值，分别取120 s、240 s、300 s采样点的实际值与仿真值进行对比，如表3所示。

表3 给定采样点的修正Allan方差值对比

从表3 可知，仿真钟差噪声的修正Allan方差值与实际钟差噪声相差不大，最大为10－25左右，最小为10－26左右，说明仿真得到的钟差噪声是符合实际钟差噪声特性的。

3 结束语

本文从卫星钟差仿真的重要性出发，结合二次多项式钟差模型，使用修正Allan方差对实际钟差数据的频域稳定度进行评估，分析了不同卫星钟的钟差噪声特性。使用仿真噪声数据对实际钟差数据进行反演拟合，在已知两者的修正Allan方差值的基础上得到拟合参数，从而获得高逼真度的卫星钟差仿真模型。通过与实际钟差噪声数据的对比可知，仿真得到的钟差噪声是符合实际特性的，这种卫星钟差的仿真方法是切实可行的。

［1］张守信.GPS 卫星测定定位理论与应用［M］.国防科学技术大学出版社，1996.

［2］黄观文，张勤，王继刚.GPS 卫星钟差的估计与预报研究［J］.大地测量与地球动力学，2009，29(6）.

［3］王潜心，李黎，龚佑兴.GPS 卫星钟的特性与预报研究［J］.测绘科学，2010，35 (2）.

［5］M.Y.Shin，C.Park，S.J.Lee.Atomic Clock Error Modeling for GNSS Software Platform［J］.IEEE 2008，71-76.

［4］Allan D W，Barnes J A.A modified Allan variance with increased oscillator characterization ability［C］// Proc.35th Annual Frequency Control Symposium，Fort Monmouth，NJ，1981:470-475.

［5］焦月，寇艳红.GPS 卫星钟差分析建模及仿真［J］.中国科学:物理学力学天文学，2011，41(5）:596-601.