横流中射流及其温度标量输运大涡模拟

鲁 俊,王玲玲,曹小红

(1.张家港市水利局,江苏张家港 215600;2.河海大学水利水电学院,江苏南京 210098)

横流中射流及其温度标量输运大涡模拟

鲁 俊1,王玲玲2,曹小红1

(1.张家港市水利局,江苏张家港 215600;2.河海大学水利水电学院,江苏南京 210098)

将动力拟序涡黏性亚格子应力模型拓展到温度标量亚格子模型中,数值模拟了横流条件下有、无温度标量场作用的射流,得到的横流条件下浮力射流的温度和速度分布与Anwar的试验值吻合一致。在此基础上,分析了有、无温度标量场作用下射流回流区域大小和射流轨迹线特性,对比分析了回流区域内涡心和分离点处湍动能和耗散率、拟涡能以及边界层处拟序结构等湍流特性。计算结果表明:温度场的作用使射流的回流区域增大,射流速度轨迹线高度增加,回流区域内湍流的湍动能增加,边界处拟序结构的周期性不如无温度场时明显。

射流;横流;大涡模拟;温度场;拟序结构

在实际工程中常遇到废温水向河流中排放等问题。从水力学角度来看,这类问题可以概化为横流中的射流及其标量输运问题,因此,对此进行系统研究具有重要的理论意义和实际应用价值。

许多研究者对此类问题做了很多试验及理论和数值模拟研究,如文献[1-4]研究了射流轨迹线等宏观分布特性,但未能给出瞬时流场分布特性;韩会玲等[5]采用雷诺时均方程数值分析了横流中射流,受雷诺时均方程的局限,仅能对射流的轨迹线等宏观特性进行分析,未能给出射流发展的整个瞬时过程。近几年来,随着计算机运算能力的快速提升和大涡模拟理论的成熟,越来越多的研究者开始用大涡模拟技术来研究这一问题,如Majander等[6]利用经典Smagorinsky亚格子模型模拟了横流中圆孔射流及其标量输运问题,发现采用经典Smagorinsky亚格子模型在靠近壁面处误差较大;Wegner等[7]用大涡模拟技术分析了横流中射流掺混图像特性,但没有定量分析射流湍流特性。

由于经典Smagorinsky亚格子模型模拟射流存在较大误差以及在壁面处采用壁面函数或者采用涡黏性衰减函数来模化涡黏系数等不足,文献[8]利用湍流的拟序结构,构造了新的亚格子应力模型,其模型系数采用动力模式来求解,并成功地应用于复杂环境中射流数值模拟[9-10]。本文利用此亚格子应力模型数值模拟横流条件下的射流,并定量分析有无其标量输运对射流湍流特性的影响。

1 数学模型的建立

1.1 控制方程

对不可压缩的流体流动及其温度输运,可用连续方程、动量方程、能量方程和状态方程来控制。在大涡模拟理论中,用空间滤波把求解的变量分为能直接求解的大尺度量和需要模化的小尺度量。在Bousineq的假设下,其在一般坐标下的空间滤波后的数学控制方程[11]为

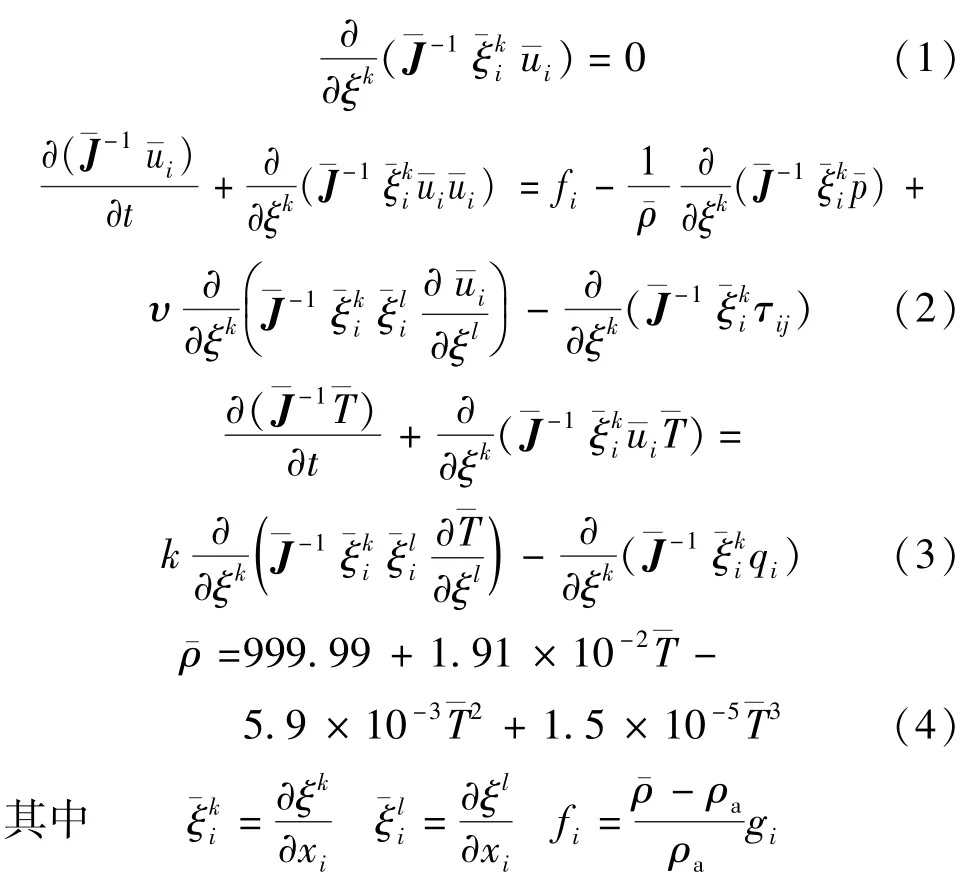
式中:ξk、ξl为空间中任意坐标(k=1,2,3;l=1,2, 3);J-1为Jacobian矩阵;ui为直角坐标下速度分量; p为静水压强;υ为流体运动黏性系数;t为时间; τij为亚格子尺度应力;T为温度;k为分子扩散系数,,其中Pr为分子普朗特数;q为标量亚格i子输运项;ρa为环境流体密度;ρ为射流密度;gi为重力加速度;xi为直角坐标。

亚格子尺度应力τij采用由文献[8]提出的考虑拟序结构作用的动力拟序涡黏性亚格子模型模化,类似可把上述模型拓展到标量亚格子输运项qi模化,其结果如下:

式中:Cs为Smagorinsky常数;Δ为滤波尺度,定义为Δ=1/2;νt为湍动扩散系数;为反对称变形张量;为对称变形张量;α为加权权重,取α= 0.5;Prt为湍动普朗特数,同Smagorinsky常数Cs一样,其值一般不是一个常数,是个动态变化的值,本文利用动力模式的思想来确定。

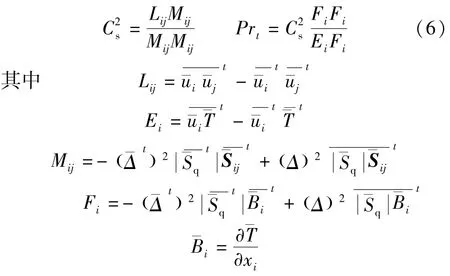
用式(6)确定系数Cs在空间分布变异较大,从而导致νt在空间变化剧烈,这种剧烈的变化往往会导致数值计算的不稳定。为此采用文献[8]提出的加权时间平均法:

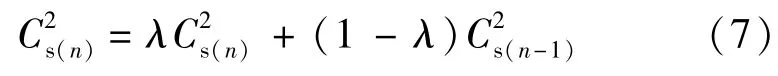
同理,湍动普朗特数采用加权时间平均法如下:

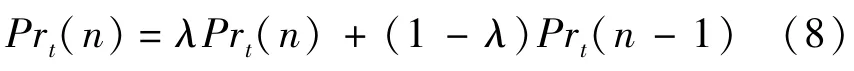
式中:λ为时间加权值,数值计算表明λ取值为0.65最佳;下标(n-1)表示上一时刻。

1.2 数值求解方法

为了计算不规则的区域和自由表面,采用垂直σ坐标,把一般坐标下的方程采用以下方程转化为σ坐标:

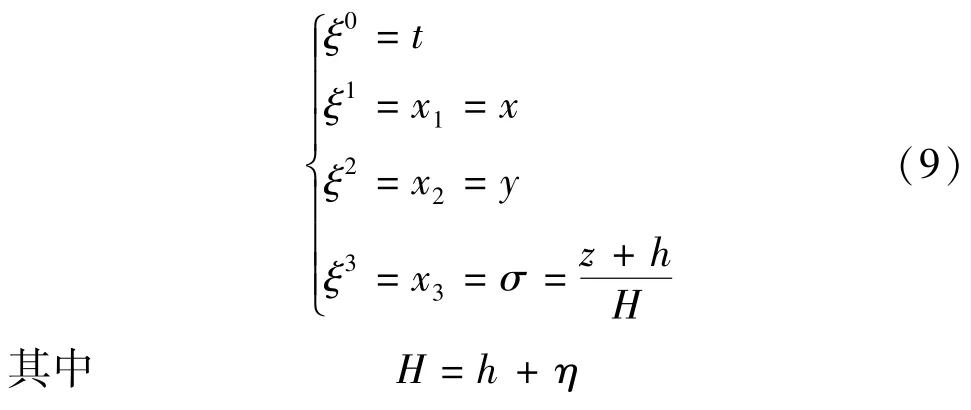
式中:η为自由表面波高;h为静止水深。当z在-h ～η之间变化时,σ在0～1之间变化。把式(9)进行微分求导代入式(1)、式(2)和式(3),得到σ坐标的表达式,详细推导过程见文献[8,10],数值方法采用分步法,动量方程分为3个计算过程,即对流计算过程、扩散计算过程和压力传播过程;能量方程分为两个计算过程,即对流计算过程和扩散计算过程。压力的变化通过求解Poisson压力方程来满足连续方程得到,采用计算速度快、鲁棒性好的CGSTAB方法求解。程序采用Fortran语言编写。

1.3 边界条件

a.进口边界条件分为横流进口条件和射流进口条件。为了快速产生湍流,横流和射流进口速度场采用给定的平均流速再加由方位角产生的随机扰动给定脉动速度;射流进口温度场采用给定的平均温度再加由方位角产生的随机扰动给定脉动温度。

c.壁面条件。底部固壁采用不可滑移边界条件;侧向固壁采用可滑移边界条件。

d.自由表面。采用Lagrange-Euler法求解以下标高函数捕捉自由表面形状:

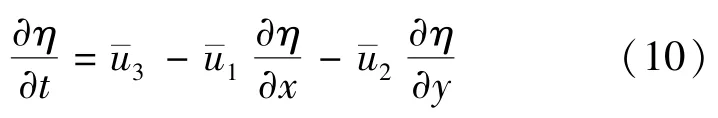
2 数值模拟结果及分析

2.1 数学模型验证

应用上述模型和计算方法对Anwar[13]试验成果进行对比验证。试验水槽长10 m,宽0.6 m,高1.2m。76℃的热水从射流窄缝处垂直射向温度为12℃的环境流体。射流孔口宽为0.01m,长为0.6 m。环境流体采用流量为0.23m3/s泵循环。选取其射流比R=W0/Ua=2的浮力射流工况(简称CR1工况)进行验证,其中W0为射流的垂向速度,Ua为横流速度。

计算区域长取为6 m,为了减少宽度方向网格数量和采用可滑移边界条件,计算宽度仅取为0.1 m,高为1.0 m。经网格无关性要求验证后,在x(槽长)方向、y(槽宽)方向和z(高度)方向(即σ方向)分别采用309、11、85网格划分,其中,在x方向射流口宽度d范围内均匀布置11个网格节点,非均匀网格中最小网格尺度为0.002,最大网格尺度为0.083;y方向采用均匀网格;在z(垂线)方向采用不均匀网格划分,最小网格尺度为0.003,最大网格尺度为0.032。时间步长Δt=2.5×10-4s,满足计算过程对流稳定性条件和扩散稳定性条件,计算时间为40 s。计算在CPU主频为3.0 G、内存为2 G的计算机上计算约耗时300 h。

图1为时间平均下的温度计算值和试验值的对比。为了和文献中[13]中坐标取值一致,图中相对长度δ按文献[13]方式定义为垂直断面温度T-Ta

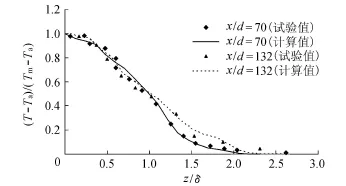
图1 平均温度大小分布

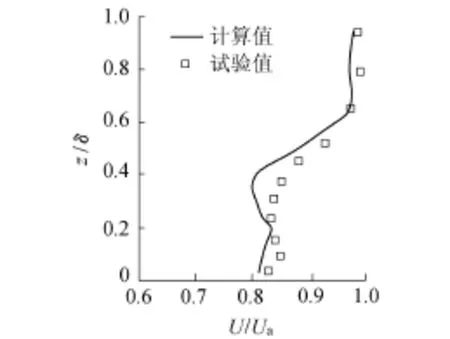
图2 平均速度大小分布

2.2 计算结果分析

为了进一步对比分析温度场对射流特性的影响,计算同样工况下无温度场的湍动射流(简称CR2工况)。

2.2.1 速度场、雷诺应力场和温度场分析

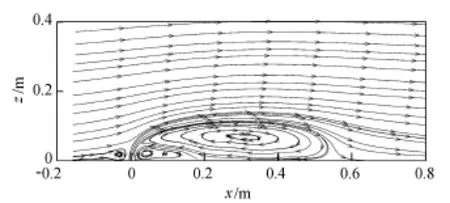
图3 CR1工况垂直平面流线

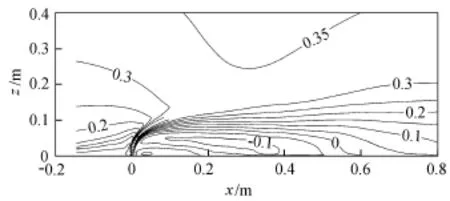
图4 CR1工况垂直平面x方向速度等值线(单位:m/s)

图3 为CR1工况时间平均下浮力射流流线。从图3可知,环境流体受到窄缝射流的阻滞而形成绕流,因此在射流的上边缘和下边缘形成不对称的压强分布,此不平衡力使射流发生弯曲,弯曲程度受到来流速度和射流速度及其温度差产生浮力的综合影响。另外,图3还显示在射流前后下端区域呈现出三角形状角涡,同时在射流背水面呈现出大范围的回流区,x方向流速为负值,如图4所示。同时在横流主流区和回流区之间形成一个强的切应力区,如图5所示。图6为时间平均下温度等值线,可以看出,在射流出口附近,由于射流的初始动量较大,最大温度在垂向上逐渐抬升,直至某一距离后,由于射流的动量作用减小,最大温度值受到横流和回流区的负速度影响,逐渐降落,直至贴壁,并入侵回流区。这一现象也为韩会玲等[5]用RANS双方程数值模拟得到。结合Anwar[13]试验成果发现,随着射流比的减小,射流背水面的回流区域减小,流线的弯曲程度越大,流动越贴近壁面;同时,横流的对流速度作用增大,在射流出口处射流温度的衰减也越快,环境流体与射流流体的温度掺混稀释能力也越强。对比图3和图7,可以明显地得出温度场中正浮力作用使回流区域增大的结论。

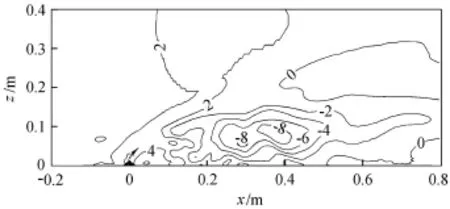
图5 CR1工况垂直平面雷诺应力等值线(单位:Pa)

图6 CR1工况垂直平面温度等值线(单位:℃)

图7 CR2工况垂直平面流线

2.2.2 射流轨迹线、湍动能、耗散率和拟涡能分析

为了进一步研究温度标量场对射流轨迹线的影响,图8给出了射流边缘速度内外轨迹线。由图8可知,约在z/d=0～7的范围内,浮力射流和湍动射流的速度内外轨迹线重合,说明在射流出口附近动量作用远远大于浮力作用;越远离射流,浮力作用越明显,射流的速度内外轨迹线都向上移动,同时速度外轨迹线附近温差大而形成的浮力作用比速度内轨迹线附近形成的浮力作用强,致使在温度场浮力作用下,CR1工况的速度内外轨迹线之间的距离比CR2工况的速度内外轨迹线之间的距离大。图9为CR1工况最大速度轨迹线、最大温度轨迹线和CR2工况最大速度轨迹线,可以看出在温度场的正浮力作用下最大速度轨迹线高于无温度场浮力作用下最大速度轨迹线,最大速度轨迹线与最大温度轨迹线不重合,最大温度轨迹线低于最大速度轨迹线。值得一提的是约在z/d=0～7的范围内,浮力射流和湍动射流的最大速度轨迹线重合,这从另外一个角度说明在射流出口附近动量作用远大于浮力作用。

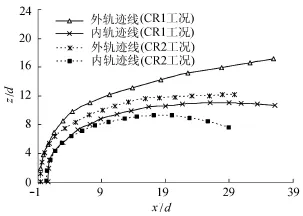
图8 射流速度内外轨迹线

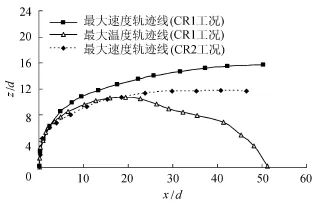
图9 射流最大速度和最大温度轨迹线

图10 涡心和分离点处垂直断面湍动能

图10 和图11分别为CR1工况和CR2工况涡心和分离点处垂直断面的湍动能和耗散率。从图10可知,无论是否受温度影响,回流区域以上的湍动能k沿z轴正向逐渐减小,符合湍流湍动能逐渐衰减的物理机制。但在涡心处不受温度影响的湍动能明显大于受温度影响的湍动能,在分离点处两者却相反。而涡心和分离点处不受温度影响的耗散率ε均大于受温度影响的耗散率(图11),这说明符合温度标量场在回流区域内可以延缓湍流能量衰减这一物理机制,这是由于温度场的脉动可以增加其流体湍动能,而这一点也为涡心和分离点处垂直断面拟涡能0.5Ω所证实,如图12所示。

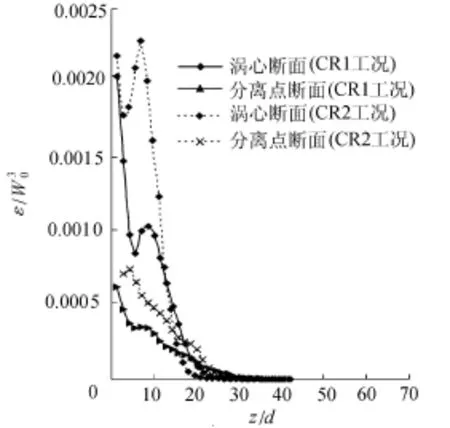
图11 涡心和分离点处垂直断面耗散率

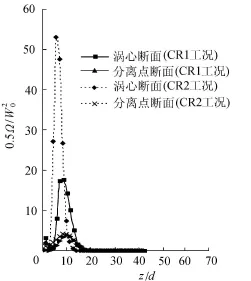
图12 涡心和分离点处垂直断面拟涡能

2.2.3 拟序结构及能谱分析

数值模拟的瞬时过程表明在回流区的分离点处,有涡旋从回流区脱离并向下游发展,如图13所示。从图13可知,近壁有大的涡团存在并逐渐向下游发展,最后脱离整个计算区域。同时图13还显示瞬时温度标量涡团和速度涡旋存在一定协同性。为了进一步研究其变化特性,在分离点的后面建立一个典型观察点A,并研究其速度分量时间序列。点A位于x=1.32 m、y=0.05 m和z=0.04 m处,即z+=zuτ/ν=85,其中为切应力。

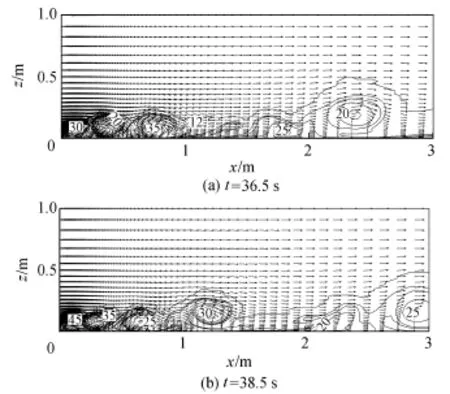
图13 CR1工况瞬时速度场和温度等值线(单位:℃)

图14 和图15分别为CR1工况和CR2工况下点A处的速度分量时间序列和相应速度分量能谱图。低频处能谱可以理解为平均速度的能谱,而高频处能谱可以理解为脉动速度的能谱。对比图15中两种不同工况下速度分量能谱,可以发现约在0.2 Hz以下范围内,CR2工况中的平均速度能谱值要低于CR1工况下的平均速度能谱值,这说明有温度梯度作用下平均速度所做的功要比无温度梯度作用下平均速度所做的功要大。而约在1 Hz以上范围内,CR2工况下的脉动速度能谱值要低于CR1工况下的脉动速度能谱值,这说明有温度梯度下脉动速度的能量耗散要比无温度梯度下脉动速度的能量耗散要小,从而可说明温度主动标量场的作用可以增加湍流的湍动能并减小湍流的湍流能耗散。另外,从图15还可发现约在0.2 Hz以上,CR2工况下拟序结构的能谱值迅速增大,这说明拟序结构的作用在无温度梯度作用下增强,计算结果显示在其工况下拟序结构频率范围约在0.2～1 Hz。

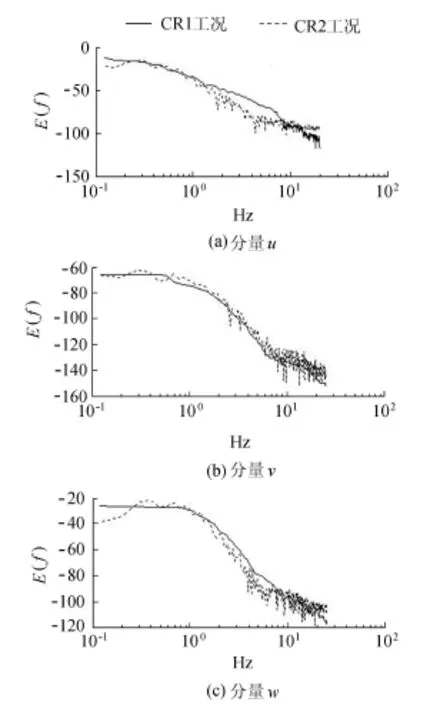
图15 点A处速度分量能谱

3 结 语

本文将动力拟序结构涡黏性亚格子应力模型拓展到温度标量亚格子模型中,数值模拟了横流条件下有、无温度标量场作用的射流。数值模拟结果表明模型在计算横流条件下浮力射流得出的温度和速度分布值与试验结果一致。在主动温度标量场作用下,射流的回流区域增大,射流速度轨迹线高度增加。温度场作用使回流区域内湍流的湍动能增加,使湍流的湍动能耗散减小,从而使湍流总能量衰减减慢。速度分量能谱图还显示了温度场的正浮力作用使拟序结构的周期性不如无温度场时明显,同时温度梯度作用使湍流的总动能量增加和能量耗散减小。

[1]ANDREOPOULOS J,PRATURI A,RODI W.Experiments on vertical plane buoyant jets in shallow water[J].J Fluid Mech,1986,168:305-336.

[2]PLESNIAK M W,CUSANO D M.Scalar mixing in a confined rectangular jet in cross-flow[J].J Fluid Mech, 2005,524:1-45.

[3]PETERSON S D,PLESNIAK M W.Evolution of jets emanating from short holes into cross-flow[J].J Fluid Mech,2004,503:57-91.

[4]CHEN K S,HWANG J Y.Experimental study on the mixing of one and dual-line heated jets with a cold crossflow in a confined channel[J].AIAA J,1991 29:353-360.

[5]韩会玲,李炜.横流中正浮力射流近区特性预报[J].河北农业大学学报,1997:20(3):112-119.(HAN Huiling,LI Wei.Prediction of characteristics for near field of positive buoyant jets in cross-flow[J].Journal of Agricultural University of Hebei,1997,20(3):112-119. (in Chinese))

[6]MAJANDER P,SIIKONEN T.Large-eddy simulation of a round jet in a cross-flow[J].Journal of Heat and Fluid Flow,2006,27:402-415

[7]WEGNER B,HUAI Y A S.Comparative study of turbulent mixing in jet in cross-flow configurations using LES[J]. International Journal of Heat and Fluid Flow,2004,25: 767-775.

[8]LU Jun,TANG hongwu,WANG Lingling.A novel dynamic coherent eddy model and application to LES of turbulent jet with free surface[J].Science in China:Series G, 2010,53(9):1671-1680.

[9]LU Jun,WANG Lingling,TANG Hongwu,et al.Large eddy simulation of vertical turbulent jets under JONSWAP waves[J].Acta Mechanica Sinica,2011,27(2):189-199.

[10]LU Jun,WANG Lingling,TANG Hongwu,et al.Numerical investigating of vertical turbulent jets in different types of waves[J].China Ocean Engineering,2010,24(4):611-626.

[11]SAUGAUT P.Large eddy simulation for incompressible flows[M].3rd ed.Singpore:Springer press,2006.

[12]LILLY D K.A proposed modification of the Germano subgrid-scale closure method[J].Physics of Fluids,1992, 4(3):633-635.

[13]ANWAR H O.Two-dimensional buoyant jet in a current [J].Journal of Engineering Mathematics,1973,7(4): 297-311.

Large eddy simulation of jets with and without temperature scalar in a current

//LU Jun1,WANG Lingling2,CAO Xiaohong1(1.Water Conservancy Bureau of Zhangjiagang,Zhangjiagang 215600,China;2.College of Water Conservancy and Hydropower,Hohai University,Nanjing 210098,China)

The jet in cross flow was simulated using a dynamic coherence eddy subgrid stress model,which was expanded into a subgrid heat flux model,under the action of temperature field.The results show that the temperature and velocity distributions of a buoyant jet in cross flow obtained from the numerical simulation are in good agreement with Anwar’s experimental data.The characteristics of backflow zones and the trajectory lines of the jets were investigated with and without temperature field.The turbulence kinetic energy and the turbulence eddy dissipation in the vortex core were compared with those of the separation point of backflow zones.The calculated results show that the areas of the backflow zones,the jet trajectory line height,and the turbulence kinetic energy increase under the action of temperature field.The period of the coherent structures near the boundary layer becomes unobvious under the action of temperature field.

jets;cross flow;large eddy simulation;scalar turbulence;coherent structures

10.3880/j.issn.10067647.2013.02.006

O358

A

10067647(2013)02002606

2012-05-15 编辑:熊水斌)

国家自然科学基金(51279050)

鲁俊(1980—),男,安徽马鞍山人,工程师,博士,主要从事湍流与环境水力学数值模拟研究。E-mail:55939818@qq.com