Engel展式逼近实数的效率
2013-06-07张振亮
张振亮
(河南科技学院,河南新乡453000)
Engel展式逼近实数的效率
张振亮
(河南科技学院,河南新乡453000)
研究了Engel展式中有无穷多个收敛因子是最佳逼近的点组成的集合,证明了几乎没有实数使得它的Engel展式中有无穷多个收敛因子是最佳逼近.另外,还给出了该集合的Hausdorff维数是大于1/2的.
最佳逼近;Engel展式;Hausdorff维数
如何用有理数更好地逼近实数一直是数论中的热点.为此,引入了各种各样的展式,例如十进制展式、连分数展式以及Engel展式.在判断一种展式在逼近实数的效率时,通常是去判断该展式所确定的收敛因子是否是最佳逼近.在本文中,主要讨论Engel展式中收敛因子为最佳逼近的情况.
1 主要结论
一个有理数a/b(b>0)称为实数x的一个最佳逼近,如果对任意的c/d≠a/b和0<d≤b,都有|dx-c|>|bx-a|成立.本文主要对Engel展式来讨论其收敛因子是否为最佳逼近.在讨论之前,先回顾一下Engel展式(详见文献[1]).
对任意的x∈(0,1],Engel变换T:(0,1]→(0,1]定义如下

那么用如下方式定义整数列{dn(x),n≥1}:dn(x)=d1(Tn-1(x)),n≥1.其中Tn表示T(T0=Id(0,1])的第n次迭代.根据Engel变换可知,对于整数列{dn}n≥1,存在某个x∈(0,1]使得在其Engel展式中有dn(x)=dn当且仅当对任意的n≥1,都有dn≥2以及dn+1≥dn.成立.
由算法(1)可得,对任意的x∈(0,1],都可以展成如下无穷序列
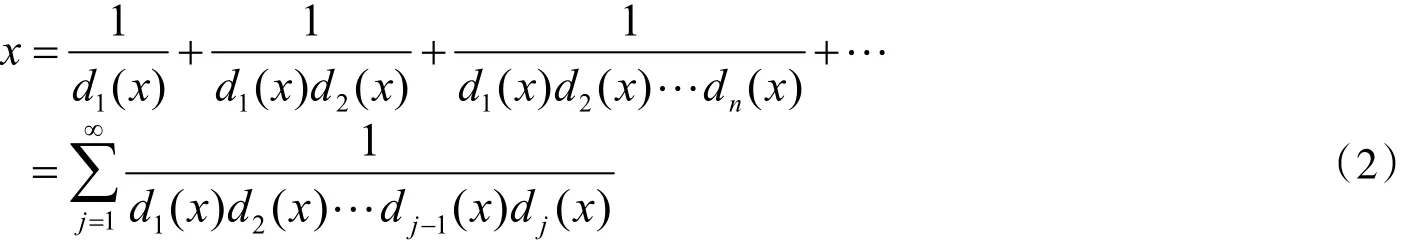
这个展式称为x的Engel展式,并把它简记为x=[0;d1(x),d2(x),…dn(x),…].
在上述背景下,把序列(2)中的前n项和记为x的Engel展式中第n个收敛因子Pn(x)/Qn(x),即

所感兴趣的是Engel展式中有无穷多个收敛因子是最佳逼近的点组成的集合,一个自然的问题是这个集合的勒贝格测度有多大.若把这个集合记为F,即
F={x∈(0,1]∶Pn(x)/Qn(x)有无穷多个是x的最佳逼近}
证明了
定理1 m(F)=0,其中m表示勒贝格测度.
另外,给出了集合F的Hausdorff维数的下界,即
定理2 dimH(F)>1/2,其中dimH表示Hausdorff维数.
在文献[2-6]中,Engel展式的遍历性质、收敛速度以及例外集的维数的刻画等方面得到了充分的研究.
2 预备知识
本节中,将规定一些记号以及回顾Engel展式中的一些基本性质.
对任意的n≥1,记Ln={(d1,d2,…dn):对任意的1≤j≤n有dj≥2以及dj+1≥dj},对任意的(d1,d2,…dn)∈Ln,令

由算法(1)容易得到[1]
引理3|In(d1,d2,…dn)|=(d1d2…dn(dn-1))-1.
在文献[7]中,Wu J证明了下面的结论
定理4对任意的v≥1,令Gv={x∈(0,1]∶d1(x)≥2,dn+1(x)≥dnv(x),对n≥1成立},则有dimHGv=1/v.
为了计算集合F的测度,需要一些有关连分数展式的展式(详见文献[8]).如通常所知,每个实数x都可以展开成如下的连分数展式

其中an(x)是正整数列并称为x的部分商,连分数中的收敛因子定义如下

引理5对任意的x∈(0,1],pn(x)/qn(x)是x连分数展式中的收敛因子,则有:①对任意的n≥1,pn-1(x) qn(x)-pn(x)qn-1(x)=(-1)n
引理6在连分数展式中,每个最佳逼近都是收敛因子[8].
3 定理1的证明
本节给出定理1的证明.
令{a(jx)}j≥1和{p(jx)/q(jx)}j≥1分别表示实数x的连分数展式中的部分商和收敛因子.对任意的0<成立有限次},那么就有

由Borel-Cantelli引理,集合A是一个零测度集合,由此,只需证明集合F∩B也是一个零测集即可.
设x∈F∩B,对任意的Qn(x),都存在某个整数i使得qi(x)≤Qn(x)<qi+1(x),那么,如果Pn(x)/Qn(x)是最佳逼近,由引理5以及引理6,可知Pn(x)/Qn(x)=pi(x)/qi(x),则有

由算法(1)可得
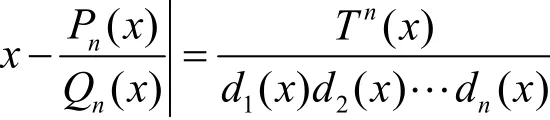
由Tn(x)>1/dn+1(x),可以得到

由引理2可知
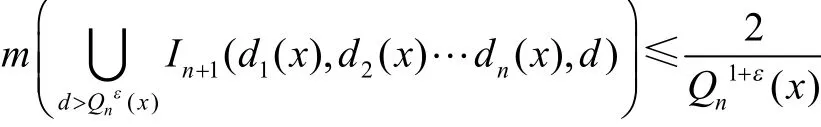
则有

4 定理2的证明
在给出定理2证明之前,先给出一个引理.
引理7令Eβ={x∈(0,1]∶d1( x)≥2,dn+1(x)≥βd1( x) d2(x)…dn(x), i.o.},则当β≥3时,有Eβ⊂F.证明:设x∈Eβ,则存在一列整数{nk}k≥1使得

那么可以得到

令

则有

那么就有
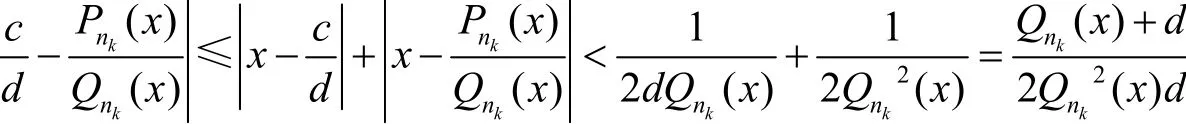
另一方面有

有了上述引理,要给出集合F维数下界,只需给出集合Eβ的下界.为此,对任意的v≥1,令Ev={x∈(0,1]∶d1(x)≥2,dn+1(x)≥(d1(x)d2(x)…dn(x))v,对n≥1无穷多次成立},容易看出G1+v包含在Ev中,则可得dimHE≥1/(v+1).
对任意的u>0,E1+u包含在Eβ中,那么可知

由u>0的任意性,则得到dimH(F)>1/2.证毕.
推论8有不可数无穷多个点使得其Engel展式中的收敛因子有无穷多个是最佳逼近.
5 小结
本文利用连分数的理论,给出了Engel展式中的收敛因子有无穷多个是最佳逼近的点组成的集合的测度意义上的刻画.证明了在测度意义下,该集合是一个零测度的集合,但其中的点却有不可数无穷多个,并且从它的维数的刻画也可以看到该集合在维数的意义下是一个不小的集合.
[1]Galambos J.Representations of real numbers by infinite series,in:lecture notes in mathematical[M].Berlin:Springer,1976.
[2]Erdós P,Rényi A,Szüsz P.On Engel’s and Sylvester’s series[J].Ann.Sci.Budapest,Sectio Math,1958,1:7-32.
[3]Galambos J.The ergodic properties of the denominators in the Oppenheim expansion of real numbers into infinite series of rationals [J].Quart.J.Math.Oxford Ser.,1970,21(2):177-191.
[4]Galambos J.On the speed of convergence of the Oppenheim series[J].Acta.Arith.,1971,19:335-342.
[5]Galambos J.Further ergodic results on the Oppenheim series[J].Quart.J.Math.Oxford Ser.,1974,25(1):135-141.
[6]Liu Y Y,Wu J.Hausdorff dimensions in Engel expansions[J].Acta.Arith.,2001,99:79-83.
[7]Wu J.How many points have the same Engel and Sylvester expansions?[J].J.Number Theory,2006,103:16-26.
[8]Khintchine A Ya.Continued Fractions[M].Groningen,The Netherlands:P.Noordhoff,1963.
(责任编辑:卢奇)
Efficiency of approximating reals for Engel expansion
Zhang Zhenliang
(Henan Institute of Science and Technology,Xinxiang 453003,China)
The set of points are investigated which convergents in Engel expansion are the optimal approximation for at least infinitely many times.It is shown that almost no points can have convergents as the optimal approximation for infinitely many times in Engel expansion.Consequently,we prove that its Hausdorff dimension is greater than 1/2.
the best approximation;Engel expansion;Hausdorff dimension
O174.12
A
1008-7516(2013)06-0029-04
10.3969/j.issn.1008-7516.2013.06.008
2013-09-25
河南省教育厅自然科学研究项目(2011A110005);河南省科技攻关项目(122102110038)
张振亮(1984-),男,河南新乡人,博士,副教授.主要从事分形几何研究.
