An Efficient Dynamic Proof of Retrievability Scheme

Zhen Mo,Yian Zhou,and Shigang Chen

(Department of Computer&Information Science&Engineering,University of Florida,Gainesville,FL 32611,USA)

Abstract Data security is a significant issue in cloud storage systems.After outsourcing data to cloud servers,clients lose physical control over the data.To guarantee clients that their data is intact on the server side,some mechanism is needed for clients to periodically check the integrity of their data.Proof of retrievability(PoR)is designed to ensure data integrity.However,most prior PoRschemes focus on static data,and existing dynamic PoRis inefficient.In this paper,we propose a new version of dynamic PoRthat is based on a B+tree and a Merkle hash tree.We propose a novel authenticated data structure,called Cloud Merkle B+tree(CMBT).By combining CMBT with the BLSsignature,dynamic operations such as insertion,deletion,and modification are supported.Compared with existing PoR schemes,our scheme improves worst-case overhead from O(n)to O(log n).cloud storage;proof of retrievability;data integrity;B+tree(CMBT).By combining CMBTwith the BLSsignature,dynamic operations such as insertion,deletion,and modification are supported.Compared with existing PoR schemes,our scheme improves worst-case overhead from O(n)to O(log n).

Keyw ords

1 Introduction

C loud storage is an online storage model.A cloud storage business provides data access and storage services with pay-as-you-go options.Developers and users can easily adapt resources to their needs and do not need to know the physical location or configuration of the system that delivers services.This elasticity,provided without any need for investment,is attracting more and more people to use cloud storage.Although it is as a promising ser⁃vice model,cloud storage also creates security problems.One of the main problems is the integrity of data stored in the cloud.After outsourcing the data to an offsite storage system and deleting the local copies,a client is relieved of the burden of storage.At the same time,it loses its physical control over the data.A cloud storage system is maintained by a third party who rarely has an infallible security system.Therefore,it is ex⁃tremely important for the clients to have an effective way of pe⁃riodically checking the integrity of their data.Many schemes have been proposed to address this issue[1]-[7].These schemes fall into two categories according to design goal:proof of retrievability(PoR)[1],[2],[4],[6]and provable dataposses⁃sion(PDP)[3],[7].The PoR scheme was proposed in[4].The design goal was to ensure that clients could retrieve data from the server side.In[3],a similar scheme,called PDP was pro⁃posed.In this scheme,clients are used to demonstrate that files are stored correctly at the server side.PDPis weaker than PoR because PDPassurance is weaker than that in PoR.PDP also does not guarantee that clients can retrieve their data in⁃tact.With PDP,clients query the server periodically,and the server returns a proof to guarantee that a certain percentage(e.g.99%)of the file is intact.However,if a very small amount of the file is lost or corrupted,clients may not be able to detect and retrieve the file intact.With PoR,clients may not detect corruption,but they can still recover the file with the help of an erasurecode.In thispaper,wemainly consider PoR.

Another important concern is support for dynamic updates.In a cloud storage system,clients should not only be able to ac⁃cess data but also dynamically modify,delete,or insert data.Most of previous works only focus on static data files[2],[4],[6],[7].Although a dynamic PoR model is proposed in[1],un⁃fortunately,thescheme'sperformanceisnot tightly bounded.

In this paper,we propose a dynamic new PoR scheme based on a modified Merkle hash tree(MHT)and Boneh-Lynn-Sha⁃cham(BLS)signature construction[8].We design a dynamic PoR model for the cloud storage system and propose a new da⁃ta structure called Cloud Merkle B+Tree(CMBT).When CMBT is combined with BLSconstruction,the worst-case per⁃formancescenariois O(log n).

In section 2,we discuss the system model and security for a typical cloud storage system.In section 3,we introduce back⁃ground research.In section 4,we present our dynamic PoR scheme.In section 5,we analyze the results of simulations run on our storagesystem.

2 System Model and Security

A typical cloud storage system includes storage servers and clients.Clients have limited storage space but have a large amount of data to be stored.Cloud storage servers have a huge amount of storage space that can be made available on a pay-as-you-go basis.Cloud storage servers are maintained by a cloud service provider(CSP)such as Amazon or Google.Cli⁃ents divide the data files into blocks that are placed into cloud storage servers.Clients delete local copies and only retain a small amount of metadata.In addition,a storage service is not static;clients can delete,insert into,or otherwise modify a block.

A CSPis a third party that does not have infallible security.We propose the following semi-trust model:In normal cases,the CSP operates correctly and does not deliberately delete or modify client data.However,management errors,Byzantine failures,and external intrusions may cause the CSPto inadver⁃tently lose or corrupt hosted data.When these errors occur,the CSP tries to salvage its reputation by hiding the true extent of dataloss.

Our new dynamic PoR scheme solves efficiency problems in existing dynamic PoR.With our scheme,file corruptions can be detected with high probability,even if a CSP tries to hide them.Files can also be dynamically updated without affecting theprobability of detectingfilecorruption.

To simplify our discussion,we treat cloud storage servers as one entity(the server)and clients as the other entity(the cli⁃ent).

3 Related Work

PoR was first formalized in[4].In PoR,“sentinel”blocks are randomly embedded in the outsourced file,and the posi⁃tion of the blocks is hidden by encryption.In this scheme,stat⁃ic data corruption can be effectively detected.However,data cannot be updated,and the number of queries a client can send isfixed.

PDPwas first proposed in[3].This scheme is used to ensure the integrity of outsourced data and makes use of RSA-based homomorphic tags.However,it cannot be used in dynamic sce⁃narios.In[7],a version of dynamic PDPis introduced,but it al⁃socannot beused in fully dynamic scenarios.

In[2],an improved PoR scheme,called Compact PoR,is in⁃troduced with rigorous security proofs[2].Using the BLSsigna⁃ture,proofsareaggregated intoa small value,and public verifi⁃cation is supported.However,this scheme is impractical and unsecure in dynamic scenarios.There are two reasons for this:1)block signatures contain the indices of blocks,and 2)replay attacks are not prevented.If a client deletes or inserts a block with index i,then any block with index j,j＞i will have to change its index to j-1 or j+1.The client has to re-sign all the blocks whose indices have been changed,and this makes the scheme impractical in termsof dynamic updates.

In[1],another dynamic PoR scheme is defined.In this scheme,the BLSsignatureand MHTaremodified sothat integ⁃rity can be verified in cloud storage[9].In order to build an MHT over a large piece of data(e.g.a file),the client first di⁃vides the file intodata blocks mi,1≤i≤n and computes the hash value for each block.This hash value is given by ni=H(mi).We call nithe“block tag”of mi.Then,the client con⁃structs a binary tree whose leaf nodes are the hashes of the block tags.Nodes that are further up in the tree are the hashes of their respective children.Finally,the client generates a root R based on the MHT and takes the signature of the root sigsk(R)asmetadata.

Using a classic MHT is inefficient.After inserting or delet⁃ing some blocks,the MHT becomes unbalanced.If the client keeps appending blocks to the tail of the file,the height of the tree increases linearly.As a result,the worst-case scenario in an integrity check would be O(n)instead of O(log n)[1],where n isthetotal number of blocks.

4 Our Scheme

4.1 Overview

Our schemecomprises three stages:1)preprocessing,2)ver⁃ification,and 3)updating.In the preprocessing stage,the cli⁃ent encodes the file with an erasure code and divides the en⁃coded file into blocks.This is done before the file is out⁃sourced to the server.Then,an authenticated data structure is constructed,and the metadata is generated.The client only keeps the metadata and outsources other data to the server.In the verification stage,theclient periodically checkstheintegri⁃ty of its data.This is done after outsourcing to the server.The client queries the server with a subset of the data blocks and requires the server to provide a proof.By verifying the proof against the metadata,the client can accurately detect file cor⁃ruption.In the update stage,the client sends the server a re⁃quest to update the file.After each update,the server proves to theclient that theupdatehasbeen successful.

4.2 Model

Our scheme can bedescribed by the following algorithms:

·KeyGen(1k)→(pk,sk).This is an algorithm run by the cli⁃ent.The input is a security parameter,and the output is a public key pk and a private key sk.The client stores sk and sends pk totheserver.

·Prepare(sk,F′,Ftags)→(ɸ,sigsk(ɭ(R)),CMBT).This algo⁃rithm is executed by the client.The input is an encoded file F′,which is created by a sequence of blocks mi,0≤i≤n;the block tag set Ftags={H(mi),0≤i≤n};and sk.The output is a signature setɸ,which is an ordered collection of signatures{σi}on{mi},0≤i≤n.We define the signature set in subsection 4.3.The client also constructs a CMBT by using Ftagsand signs the label value of root sigsk(ɭ(R))by us⁃ing sk.

·GenChallenge(n)→Q.Thisalgorithmis executed by thecli⁃ent.The input is the total number of blocks,and the output is a query Q that contains a set of IDs I={i1,i2,...,ik}.The query is sent to the server as a request to verify the integrity of blockswith index i,for i∈I.

·GenProof(Q,CMBT,F′,Ftags,ɸ)→P.Thisalgorithmisexe⁃cuted by the server.The input is Q,CMBT,F′,Ftags,andɸ.The output is a proof P that allows the client to check the in⁃tegrity of the blocks in Q.

·Verify(pk,Q,P,ɭ(R))→(TRUE,FALSE).This algorithm is executed by the client.After receiving theproof P,thecli⁃ent checks the integrity of blocks in Q.The client then out⁃puts TRUE if the integrity of the blocks is confirmed;other⁃wise,it outputs FALSE.

·UpdateRequest()→Request.This algorithm is executed by the client.Nothing is input.The output is an update request R that contains an Order∈{Insert,Delete,Modify}and an index number i.If Order is Modify or Insert,then R should alsocontain anew fileblock m*and itssignatureσ*.

·Update(F′,Ftags,ɸ,R)→(Pold,Pnew).This algorithmis exe⁃cuted by the server.After receiving the R from the client,the algorithm takes F′,Ftags,ɸ,and R as input and outputs twoproofs:Poldand Pnew.

·UpdateVerify(Pold,Pnew)→(TRUE,FALSE).This algorithm

is executed by the client.With Poldand Pnew,the client out⁃puts TRUE if the server's behaviors are honest in the up⁃date process;otherwise,it outputs FALSE.

4.3 Preprocessing

Before outsourcing the files to the server,the client encodes F to F′using an erasure code.Then,the client runs KeyGen(1k)to create a pair of keys and uses Prepare(sk,F,Ftags)to generateɸ,a CMBT,and the metadata sigsk(ɭ(R)).

We use the same BLSsignature as that defined in[1].For a bilinear map e:G×G→GT,sk and pk are defined as x∈Zpand v=gx∈G,respectively,where g is a generator of G.For each mi,i∈[1,n],the signature on miis defined asσi=[H(mi)umi]x,where u is a generator of G.We denote the set of the signature asɸ={σi},1≤i≤n.

MHT[9]has been widely used for checking memory integri⁃ty[10],[11]and certificate revocation[12],[13]because it is easy to realize and has O(log n)complexity in both worst-case and usual scenarios.However,using the classic MHT in cloud storage may cause problems(section 3).Therefore,we develop an authenticated data structure based on a B+tree and MHT.

1A B+tree[14]differs froma Btree in thefollowingthreerespects:

1.A B+tree has twotypes of nodes:index and data.Index nodes storekeys,and data nodesstore elements.A Btreeonly has datanodes.

2.Datanodes in a B+treearelinked by a doubly linked list whereasdatanodes in a B tree are not linked.

3.The capacity of data nodesand index nodes can differ in a B+treewhereasthecapacity of nodes in a Btreeshould bethesame.In a B+treeof order n,index nodes(except for the root node)can hold a maximumof n-1 keysand aminimumof「n=2-1■keys.Each datanodecan contain amaximumof c elementsand aminimumof「n=2■elements(c and n can differ).The root nodecan hold amaximumof n children and a minimumof twochildren.We call this new structure a cloud Merkle B+tree(CMBT).We choose a third-order B+tree1and require each data node tostorethreeelementsat most.

We treat the sequence of block tags H(m1),H(m2),...,H(mn)as elements and insert them into a B+tree sequentially.Then,weobtain a B+tree(Fig.1)and basethe CMBTon it.

For each node w in a CMBT,the followingvalues are stored:

·left(w),middle(w),and right(w).For an index node,these variables represent the left child,middle child,and right child of the node,respectively.If the node only has two chil⁃dren,then right(w)will be 0.For a data node,these variants represent the elements the node stores(from left to right).If a corresponding position has no element,0 is set.

·r(w).This is the rank of node.For an index node w,r(w)stores the number of elements that belong to the subtree whose root is w.For a data node w,r(w)stores the number of elements that belong to w.Fig.1 shows the rank for each node.The rank for node d1is 2 because from d1we can visit two elements:H(m1)and H(m2).

·t(w).Keys are not stored in an index node because the CMBT does not need to be searched.Instead,the type of the nodeisstored as t(w),where

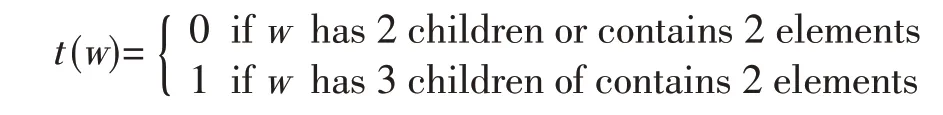
·ɭ(w).This is the label of node.To defineɭ(w),first we de⁃fine a collision-resistant hash function h(*)that has two in⁃puts:h(a,b)=h(a‖b),where‖means concatenation.Then,we extend the function to more than two inputs:h(a1,a2,...,an-1,an)=h(a1‖a2‖...‖an-1‖an).Then,ɭ(w)=h(ɭ(left(w)),ɭ(middle(w)),ɭ(right(w)),t(w),r(w).For each element e that contains a block m,the value of the element is given byɭ(e)=h(H(m)).

With above definitions,the client can construct a CMBT and obtain the label value of the root R.Then,the client signs theroot labelɭ(R)using itsprivatekey:sigsk(ɭ(R))←(ɭ(R))sk.Next,the client outsources F,ɸ,the CMBT,and sigsk(ɭ(R))to the server.

4.4 Query

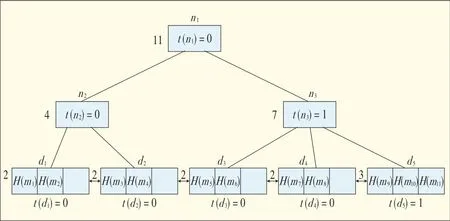
▲Figure1.A cloud Merkle B+tree.

Suppose F′,ɸ,CMBT,and sigsk(ɭ(R))have been out⁃sourced to the server.The client only stores the metadata and number of blocks n,and it generatesaquery tocheck theinteg⁃rity of a series of random blocks whose index numbers belong to the set I={i1,i2,...,ik}.The client uses the GenChallenge(n)→Q algorithmto generate a Q.For each index number i∈I,the client chooses a random element vi←Zp.Then,Q={(i,vi)},i1≤I≤ik.

After receiving Q,the server executes GenProof(Q,CMBT,F,Ftags,ɸ)→P to generate a proof P by first computingμand σ:

Then,the server generates a sequence of messages for each block tag H(mi)in the block tag set S={H(mi),i∈I}.Sup⁃pose{w1,w2,w3,...,wh,wh+1}is the path from the root node to the element H(mi),where i∈[i1,ik];h is the height of the CMBT;and wjistheparent node of wj+1.For each node wj,j∈[1,h],the server provides a message Mjthat is a 2-tuple val⁃ue.We define nj+1and n′j+1as neighbors of wj+1,and n(j+1)is alwaystothe left of n′j+1.We denote T asaset of nodal informa⁃tion that isgiven by

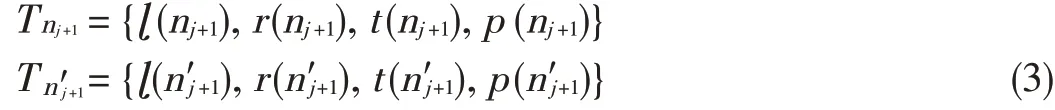
If wj+1has only one sibling,then T(n′j+1)=NULL.The loca⁃tion relationship between nj+1and wj+1isgiven by

Therefore,amessagefor wjisgiven by

The message sequence for element H(mi)is given byγi={M1,M2,...,Mh},and for all elements in set I,the message set isgiven byΓ={γi1,...,γik}.Therefore,P={μ,σ,S,Γ}.

If theclient only wantsto check theintegrity of oneblock in⁃stead of a group of blocks,the proof of a single block with in⁃dex i isgiven by

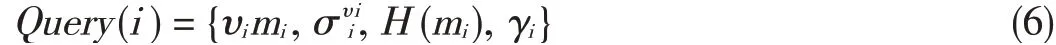
4.5 Verification

After receiving proof P from the server,the client executes Verify(pk,Q,P,ɭ(R))(Algorithm 1)to check the integrity of the blocks whose indices belong to I.In Algorithm 1,{w1,w2,w3,...,wh,wh+1}is the node sequence from the root to the ele⁃ment H(mi).To compute wj,1≤j≤h,the client first deter⁃mines how many children wjhas.Then,the client inputs the children's values and their locational relationship p(1)into the GetValue function in order to compute wj.The computa⁃tion continues until the root node isreached.During the proce⁃dure,the client can verify the index number idx of the block tag H(mi).

Algorithm1Verify(pk,Q,P,ɭ(R))→(TRUE,FALSE)1:Verify e(σ,g)=e(∏ik H(mi)vi·uμ,υ)2:for i from i 1 to ik do 3:γi={M 1,M 2,...,M h},M j={T ,T n′j+1}4:T ={ɭ(n′j+1),r(n′j+1),t(n′j+1),p(n′j+1)}5:Tn′j+1={ɭ(n′j+1),r(n′j+1),t(n′j+1),p(n′j+1)}6:idx=1 7:for j from h down to 1 do 8: if T n′j+1≠NULL then 9: r(wj)=r(w j+1)+r(n j+1)+r(n′j+1)10: t(w j)=1 11: ɭ(wj)=GetValue(T,T n′j+1)12: if p(n′j+1)=0 then 13: idx=idx+r(n′j+1)14: end if 15: else 16: r(wj)=r(w j+1)+r(n j+1)17: t(w j)=0 18: ɭ(w j)=GetValue(T)19: end if 20: if p(n j+1)=0 then 21: idx=idx+r(n j+1)22: end if 23:end for 24:ifɭ(w 1)=ɭ(R)AND idx=i then 25: if i=ik then 26: return TRUE 27: end if 28:else 29:return FALSE 30: end if 31:end for? i=i 1 n j+1 n j+1 n j+1 n j+1

4.6 Updates

Here,we show that our scheme can be used to delete,insert into,or otherwise modify blocks.We assume that F′,ɸ,and CMBThavebeen generated and stored in theserver.

Suppose the client wants to update the j th block,1≤j≤n.The client first executes UpdateRequest()→Request to generate an update request and send it to the server.Upon re⁃ceiving the modification request,the server updates the block and executes Update(F′,Ftags,ɸ,R)to generate Poldand Pnew.With Poldand Pnew,the client executes UpdateVerify(Pold,Pnew)toensurethecorrectnessof theupdate.

Suppose a client wants to modify the j th block,1≤j≤n,from mjto m′j.The client generates an update request Re⁃ent computes the new root Rnewusing Pold.The server only needs to send Pnew=R′,which is the new root node to the cli⁃ent.After verifying the correctness of R′,the client signs the new root sigsk(ɭ(R′))and sendsit back.quest={Modify,j,m′j,σ′j}and sends it to the server.The serv⁃er updates the block,reconstructs the CMBT,and generates the proof Pold=Query(i)(6).With Pold,the client can check the integrity of mj(Algorithm 1)and construct a partial CMBT(Fig.2).The partial CMBT is constructed from the query on the CMBT in Fig.1.The client obtains enough information to update the CMBT from the partial CMBT.In this case,the cli⁃

▲Figure2.Partial CMBT constructed from P old=Query(4).

The procedure for insertion is similar to that for modifica⁃tion.The only difference is that when a new element is insert⁃ed into a data node that already contains three elements,the data node splits in two.The procedure keeps going until one in⁃dex node has only two children or we need to generate a new root and increase the height of the tree by one.With the partial CMBT constructed from Pold=Query(i),the client has enough information to compute Rnew.After verifying the correctness of R′,the client signsthe new root sigsk(ɭ(R′))and sendsit back.

The procedure for deletion differs from that for insertion and modification.Deletingan element froma datanodewith twoel⁃ements makes the data node deficient.Therefore,borrow or merge operations need to be performed to keep the tree bal⁃anced[14]Because the partial CMBT is constructed from the Pold,the client may not acquire enough information to finish these operations and compute Rnew.Accordingly,the server needs to send another Pnewto help the client verify the correct⁃ness of R′.Here,we define another algorithms:Algorithm Querynew(i)is used to return the proof of the i th element in the updated CMBT.

Using Pold,the client can generate a partial CMBT that con⁃tains the node sequence{wi}and its siblings{ni,n′i},i∈[1,h+1].The element that the client wants to delete is denoted wh+1.Therearethreecasesof deletion:

1)If the leaf node whcontains three elements,then the client only needs to delete wh+1and generate R′based on Pold.Oth⁃erwise,the client keeps searching the node sequence from whto w1until it finds wj,j∈[1,h].The right or left sibling nodesof wjhas three children or wjitself hasthree children.

2)If one sibling of wjhas three children,then the client needs to borrow a child from its sibling to generate a new node.However,Polddoes not contain the information of this child.The client will therefore use Querynew(i)and Query(k)toac⁃quire additional information to delete wh+1and generate a new root.The index number of the element that belongs to the subtree(whose root is the sibling node)is given by k.The client can obtain k easily from Pold.The information from Querynew(i)can beverified by Pold.

3)If wjhas three children,the client deletes the element and merges two children.By using Querynew(i),the client ac⁃quires enough information to generate the new root.If the client cannot find the node until it reaches the root,the cli⁃ent generates a new root.In this case,the CMBT height de⁃creases by one.Here,we do not provide the complete algo⁃rithm,but thecomplexity of thedeletion is O(log n).

5 Simulation Results

In Table 1,we show the performance of our scheme and that of existing PoRschemeson afeature-by-featurebasis.Our ex⁃periment ran on a system with an Intel Core 2 2.53 GHz pro⁃cessor,4 GBRAM,and a 7200 RPMTOSHIBA 120 GBSATA driver.Algorithmswereimplemented using C++.

▼Table1.Performanceof existing PoRschemes

We evaluated the performance of our scheme in terms of overhead.Using precious analysis,we determined that the overhead of PoRs depends on the block size and the number of messages(hashes)sent to the client.As in[3],detecting 1%file corruption with 99%confidence requires querying a con⁃stant 460 blocks.Accordingly,if the block size is fixed,perfor⁃mance is determined by the overhead in sending messages to prove the index of a block in the tree.In our experiment,we send messages using SHA1 with an output of 160 bits.The av⁃erage overhead of our scheme and that in[1]is similar;there⁃fore,in Fig.3,we show the maximum overhead of proving a block in the CMBTand MHT.

The client divides the encoded file F′into 128 blocks and uses these blocks to construct the MHT and the CMBT.Then,the client outsources F′and the MHT,and CMBT to the server.If the client keeps appending blocks to the tail of F′,the maxi⁃mum overhead between the MHT and CMBT is as shown in Fig.3.The x axis shows the number of blocks that the client appends to the encoded file after initialization.The y axis shows the overhead for proving a block in the tree.From Fig.3,the worst-case overhead for the MHT increases linearly with the number of block inserted.The worst-case overhead for MHTisgiven by O(n).

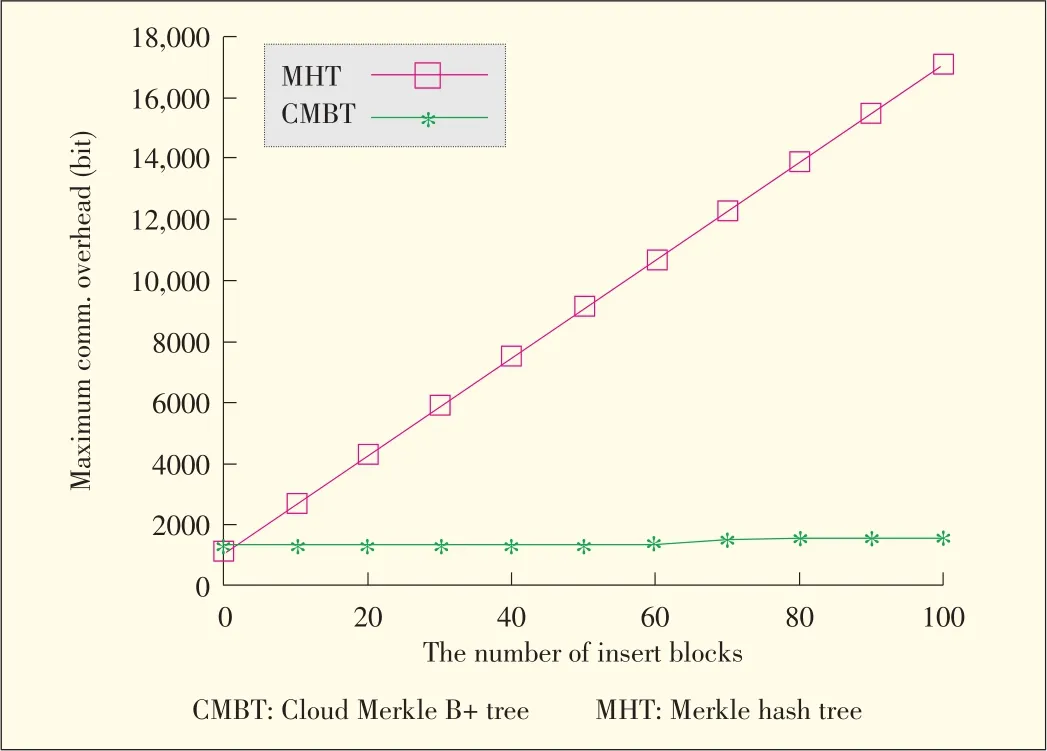
▲Figure3.Maximum overhead for proving oneblock in the MHT and CMBT.

6 Conclusion

Cloud storage creates security issues,especially in terms of data integrity.In this paper,we extend the static PoR scheme so that it can be used for dynamic scenarios.We propose anew authentication data structure called Cloud Merkle B+tree.The worst-case overhead for existing dynamic PoR scheme is given by O(n);however,the worst-case overhead for our scheme is given by O(log n).

Acknowledgment

This work was supported in part by the USNational Science Foundation under grant CNS-1115548 and a grant from Cisco Research.