框架结构内环境振动波传播规律研究
2013-06-05周福霖
叶 茂,任 珉,谭 平,周福霖,
(1.广州大学—淡江大学工程结构灾害与控制联合研究中心,广东 广州 510006;2.广州大学 抗震中心,广东 广州 510006)
国际上已把环境振动列入国际七大公害之一[1],并已开展环境振动危害[2]、污染规律[3]以及控制方法[4]等问题的研究。由于轨道交通载重大、速度快,诱发环境振动明显,所以大多研究人员在开展环境振动研究时主要以轨道交通诱发环境振动为研究对象,如:陈建国[3]、闫维明[5]、刘腾[6]、高广运[7]等采用实测方法开展了高架轨道、高速铁路、地铁、普通铁路客运专线诱发地面振动研究;冯牧[8]、陈建国[9]等就运行列车对周围建筑物振动影响进行了现场实测。但是,城市道路是城市空间内最多、最密集的交通线路,G.Lombaert[10]的调查报告指出:65%的人认为汽车产生的振动对自身的影响最大,其次是火车16%,工业活动15%,建筑施工5%。以上调查报告说明,在环境振动研究领域,城市汽车道路诱发的环境振动问题研究也是不可忽略的,但目前有关这方面的研究内容相对较少。
为此,本文以实测城市道路诱发环境振动波作为输入,此外还选取地震波作为输入与环境振动波进行对比分析,以加速度作为指标,在时域和频域内深入研究环境振动波在框架结构内的传播规律。
1 分析模型
混凝土框架结构基本分析模型如图1所示,一个三层框架,跨度4 m,首层层高3.5 m,其余层层高3 m,楼板厚度0.12 m,中间柱的截面尺寸250mm×300mm,两边柱子截面尺寸200mm×300mm,梁的截面尺寸230mm×400mm,混凝土的密度 2449 kg/m3,弹性模量20 GPa。
由于模型相对比较简单,本文采用自编有限元程序进行分析计算,其中:梁和柱采用平面梁单元模型,每个平面梁单元有2个节点,每个节点有3个自由度(两个位移和一个转角);质量矩阵采用一致质量矩阵;结构阻尼模型为Rayleigh阻尼;采用直接积分法求解。
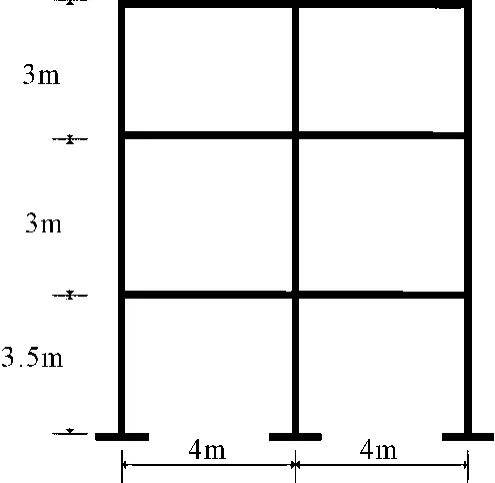
图1 框架结构模型
2 输入振动波
在输入振动波的选取上,除选取实测某综合楼的室外和地下室加速度时程作为输入环境振动波(共3条),为对比环境振动和地震波在框架结构内传播规律的差异,选择了一条地震波(El Centro波,7度,多遇地震)作为输入波。
图2给出了水平环境振动波、地震波的时程曲线和功率谱,为了能够使环境振动和地震波功率谱在同一张图上能够清晰表现,进行功率谱分析时,将所有波的最大加速度值均处理为与环境振动波-3相同,竖向亦相同。图2(a)表明环境振动波和地震波的主要频率范围存在明显差异,El Centro波的主要频率范围为0 Hz~5 Hz,环境振动波的主要频率范围在5 Hz~20 Hz之间;同时图2(a)还可清楚表明,即使是环境振动波,相互之间的频率分布范围有所不同,其中环境振动波-1的主要频率范围:10 Hz~15Hz,环境振动波-2的主要频率范围:5 Hz~10 Hz,环境振动波-3的主要频率范围:15 Hz~20 Hz。
图3给出了竖向环境振动波、地震波的时程曲线和功率谱密度函数。图3表明,竖向地震波的频率范围分布比较宽,环境振动波的竖向频率范围主要位于5 Hz到20 Hz之间,虽然各环境振动动波之间的频率范围还是有所不同,但没有水平振动明显。

图2 水平输入振动波
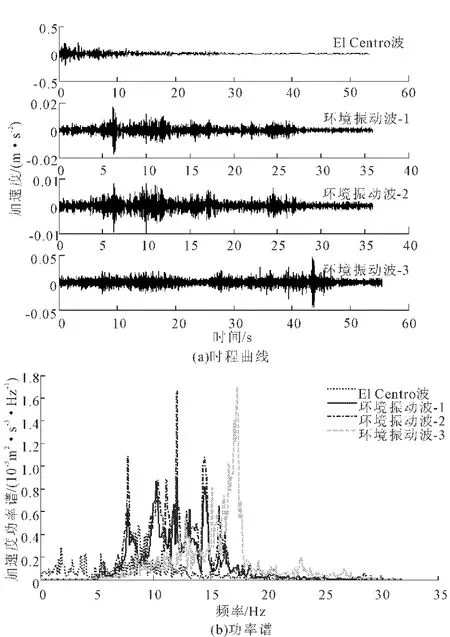
图3 竖向输入振动波
3 验证分析模型
为保证分析程序所建立模型的正确性,采用商业有限元软件建立了该有限元模型,对比模态分析结果,如表1所示,验证了程序的正确性。

表1 本文分析程序与Ansys分析模型对比
4 分析与讨论
为深入了解各种振动波在框架结构内的传播规律,本文将在时域和频域内开展深入研究,并分析楼层数对框架结构内环境振动波传播规律的影响。
4.1 时域内分析
图4给出了各层加速度峰值的变化,为能够更好地在图上反映各种振动波在框架结构内的传播规律,水平向El Centro波的分析结果已缩小到原计算结果的1/10,垂直向为1/5。就当前分析模型,图4表明:对于水平加速度,整体上来说,各楼层相对于地面水平加速度均产生放大效果,但由于输入振动波主要频率范围的不同,水平加速度在楼层间的传播特点不尽相同,其中当输入第一条和第二条振动波时,第二层比第一层和第三加速度幅值都小,输入第三条振动波和El Centro波时,随着楼层增加,振动幅值增加;对于竖直加速度,整体上来说随着楼层的增加,加速度幅值有所增加,增加的幅值较小,产生这种现象的原因在于,3层框架结构的竖向刚度比较大,输入振动波使得整个结构产生竖向整体振动。
4.2 频率域内分析
图5给出了水平和竖向加速度振级在楼层间的分布和传递,表明:振级的分布特点与加速度峰值有所不同,产生这种情况的原因在于,在计算加速度振级时,各频率点对应的加权系数不同,因此峰值加速度大,振级也不一定大,证实了规范中采用分频多值限值方法的合理性;图5中可发现,对于水平加速度振级,首层加速度振级相对于地面加速度振级会放大,但振级随楼层变化的变化规律与输入振动波有关;对于竖向加速度振级,加速度振级随着楼层的增加而增加,但放大效果不明显。

图4 加速度峰值随楼层的变化规律

图5 加速度振级曲线随楼层的变化规律
4.3 层数对框架结构内振动传播的影响规律
为分析高宽比对环境振动诱发结构振动的影响,本文分别对3层框架、6层框架、10层框架和16层框架进行分析,在进行分析时,只是层数不同,其余参数均与3层框架分析模型相同,各分析模型的前三阶振型周期见表2。
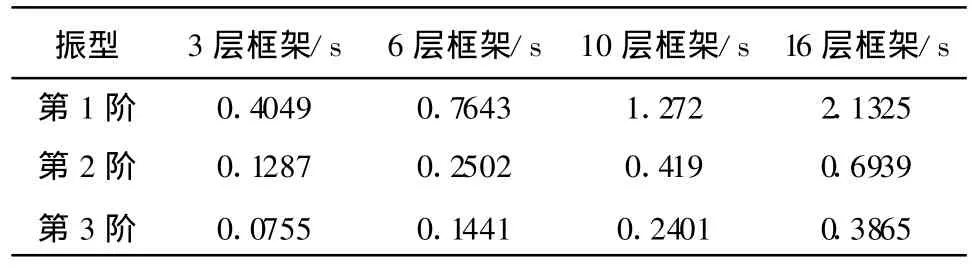
表2 框架模型振型周期
图6给出了不同输入振动波作用下楼层数变化对结构加速度峰值响应的影响。图6表明:对于水平振动,通过以上表和图的分析表明随着楼层数增加,结构周期延长(见表2),伴以输入振动波特性不同,分析模型水平振动响应随楼层的变化规律不明显;当输入振动波频率分布范围与结构振型分布相近时,且结构周期较短的时候,加速度峰值都会随着楼层的增加而增加,这种现象El Centro非常明显,但随着楼层的增加,结构周期延长,加速度峰值不再是随着楼层增加而单调的增加,而是出现一定的往复,说明激发的结构振型不再绝对以第一阶振型为主;当输入振动波频率分布范围与结构振型差别较远时,如环境振动波-3,相比输入加速度波,结构上的加速度响应有所降低,且随楼层加速度峰值的变化不是非常大。
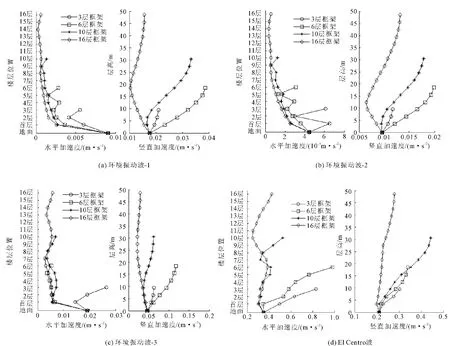
图6 楼层数对加速度峰值在框架结构内传播的影响
对于竖向加速度,当结构楼层较低时,加速度峰值都随着楼层的增加而增加,当结构增加到一定高度时,如本文的16层结构,加速度峰值随楼层的变化规律是刚开始降低,而后增加,即表明存在一个结构高宽比,使得分析结构的竖向加速度峰值响应最大,这与结构的竖向振型频率随着楼层数增加而变化有关。
5 结 论
(1)环境振动波和地震波的主要频谱范围存在明显差异,El Centro波的主要频谱范围为0 Hz~5 Hz,环境振动波的主要频谱范围在5 Hz~20 Hz之间,即使是环境振动波,它们相互之间的频谱分布范围也有所不同。
(2)对于水平加速度,各楼层相对于地面水平加速度均产生放大效果,但由于输入振动波主要频率范围的不同,水平加速度在楼层间的传播特点不尽相同;对于竖直加速度,整体上来说随着楼层的增加,加速度幅值有所增加,增加的幅值较小。
(3)振级在楼层间的分布特点与加速度峰值有不同,水平加速度振级相对于地面加速度振级会放大,但振级随楼层变化的变化规律与输入振动波有关;竖向加速度振级随着楼层的增加而增加,增加幅度较小。
(4)水平振动响应随楼层的变化规律不明显,与输入振动特性和结构自身特性有很大的关系;对于竖向加速度,存在一个结构高宽比,使得分析结构的竖向加速度峰值响应最大。
[1]高广运,孙雨明,吴世明.铁路产生的地面振动与减振[M].上海:同济大学出版社,2002.
[2]张向东,高 捷,闫维明.环境振动对人体健康的影响[J].环境与健康杂志,2008,25(1):74-76.
[3]陈建国,夏 禾,姚锦宝.高架轨道交通列车对周围环境振动影响的试验研究[J].振动与冲击,2011,30(2):159-163.
[4]Hung H H,YanY B,Chang D W.Wave barriers for reduction of train-induced vibrations in soils[J].Journal of Geotechnical and Geo-environmental Engineering(ASCE),2004,130(12):1283-1291.
[5]闫维明,聂 晗,任 珉,等.地铁交通引起地面振动的实测与分析[J].铁道科学与工程学报,2006,3(2):1-5.
[6]刘 腾,雷晓燕,刘庆杰.高速铁路沿线地面环境振动特性的实测与分析[J].华东交通大学学报,2011,28(4):19-22.
[7]高广运,李志毅,冯世进,等.秦-沈铁路列车运行引起的地面振动实测与分析[J].岩土力学,2007,28(9):1817-1822,1827.
[8]冯 牧,雷晓燕.列车引发建筑物振动现场测试及数值分析[J].铁道建筑,2011,(7):160-164.
[9]陈建国,夏 禾,曹艳梅.等.运行列车对周围建筑物振动影响的试验研究[J].振动工程学报,2008,21(5):476-481.
[10]Lombaert G.Development and experimental validation of a numerical model for the free filed vibrationsinduced by road traffic[D].The Kingdom of Netherlands:Katholieke Universiteit Leuven,2001.
