随机幅相误差对线阵方向图最高副瓣电平的影响研究
2013-06-05高坤张军袁晶
高坤张军袁晶
(西安电子工程研究所 西安 710100)
1 引言
副瓣电平是天线的重要技术指标之一,较低的副瓣电平可以减弱杂波影响、提高雷达的抗干扰能力。为确保在现代战争中夺取制空权的优势,未来的雷达系统都力求配备超低副瓣天线,从而促进了超低副瓣天线技术的发展。在超低副瓣阵列天线的研制中,不可避免的会引入误差。阵列误差可由多种因素引起,如:复权向量的幅度和相位误差,通道频响不一致性(通道失配)对系统性能的影响,信号方向估计误差,权向量的量化误差,个别阵元出现故障引起的误差等。无论是电气误差还是机械制造误差最终都可以归结为系统误差和随机误差。一般可以通过提高加工和安装精度以及试验测试等手段可以较为容易地对部分系统误差的影响进行评估和修正;而随机误差的产生不可预见(比如气候,温度,加工误差等原因引入了随机误差),以致难以修正。但不论如何,随机误差的引入最终都可以表现为阵列各个单元的幅度误差和相位误差,故需要分析幅相误差对阵列天线副瓣电平的量化影响。使最终的阵列设计既能够达到系统性能要求,又节省生产成本。
J K.Hisao[1]研究了口径幅、相误差的方差和与某方位角副瓣电平极限值的关系,类似的研究还包括文献[2,3]的内容。向广志[6]进行了超低副瓣阵列天线的公差分析,给出了特定分布随机波瓣电平与最大幅、相误差之间的关系。杨志荣等[7]研究了互耦和随机幅、相误差对副瓣电平的影响,定义了天线的误差敏感系数,通过误差敏感系数来考量互耦和误差对天线性能的影响程度。作者在前期也做了关于误差对副瓣电平的研究[10],上述这些文献都是对于某方位角上辐射电平的分析研究,缺乏对阵列最高副瓣电平的统计特性全面、细致的分析与研究。本文在计入随机误差的阵列模型的基础上,应用统计学理论分析电场方向图副瓣区某方位角上辐射电平的统计特性,之后以副瓣区各方位角的辐射电平分布来分析整个副瓣区的最高副瓣电平的统计特性,并结合计算机仿真,以切比雪夫(chebyshev)线阵为例验证公式的正确性,将计算得出最高副瓣电平的概率密度曲线与仿真得到了最高副瓣电平的概率密度直方图进行对比,理论计算曲线与仿真直方图吻合的较好。
2 阵列误差模型
设N元阵列排列在x轴上,阵元的间距为d,阵元上的电流为In,线阵模型如图1所示。
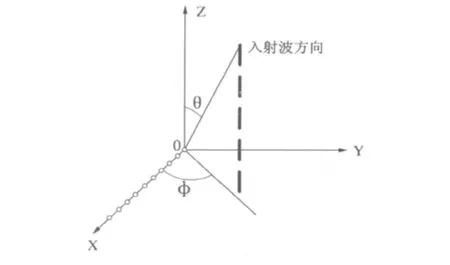
图1 N元等间距线阵模型示意图
其方向性函数可以表示为:

随机误差引入可以等效成各个单元幅度和相位的误差。计入幅度和相位误差后,使得其口径分布发生变化。
在分析计入误差后的阵列模型时,首先对误差进行了几点假定:
a.辐射元失效情况。
设fn=1代表阵列中第n个单元正常工作,fn=0则代表单元损坏。令其正常工作的概率为p,则:
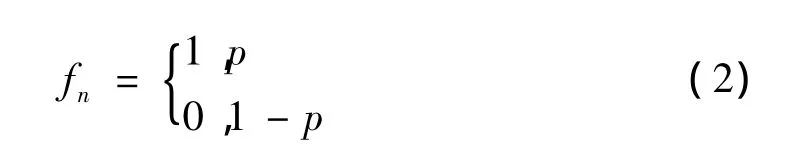
由均值定义可求得:
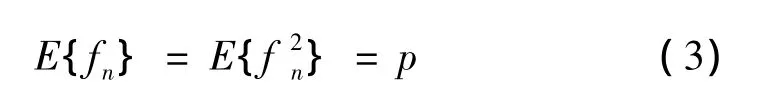
b.彼此阵元相互独立,误差互不影响。
c.引入的幅度误差为 In·Δn,相位误差为ΔΦn,其满足均值为 0,方差分别为 σ2Δ和 σ2Φ的高斯分布,即:
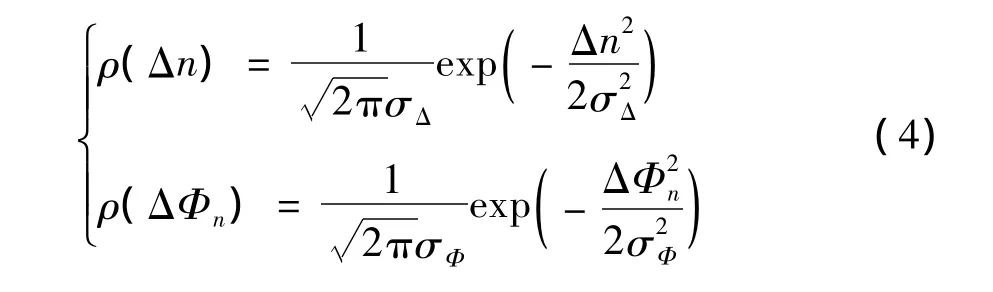

3 误差方向图的统计特性
3.1 误差方向图的均值

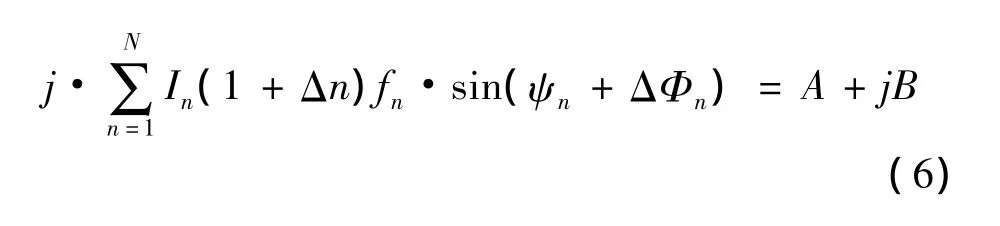

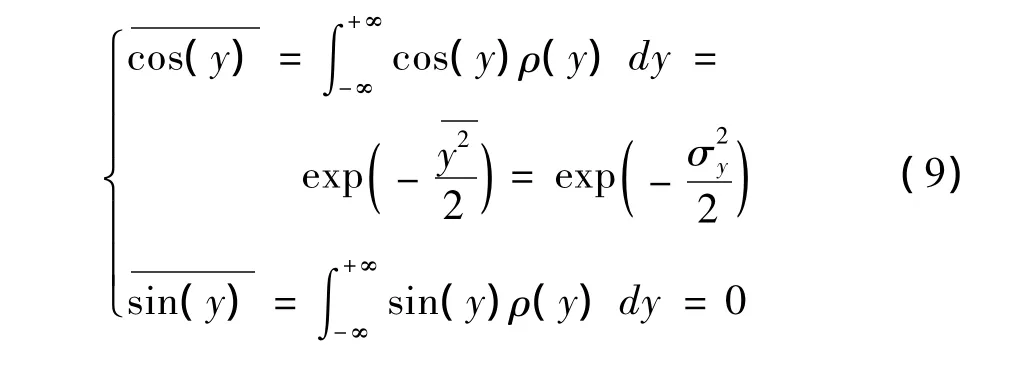
将(9)式带入(7)、(8)式,计算得出:
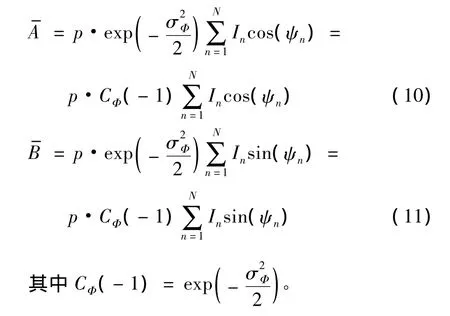
结合(6)式,最后可得:

3.2 方向性函数的统计特性
根据文献[8]所述模型,分别计算并化简可得方向性函数实部的方差、虚部方差和实部虚部的协方差σAB,其表达形式为:

在上式中的前两个表达式中,其第二项含有余弦函数,其幅度是原方向图的二次谐波,在方向图的副瓣区域里,它们的第二项比第一项小得多。此外,第三个表达式较前两个表达式相比,可忽略不计,故有:
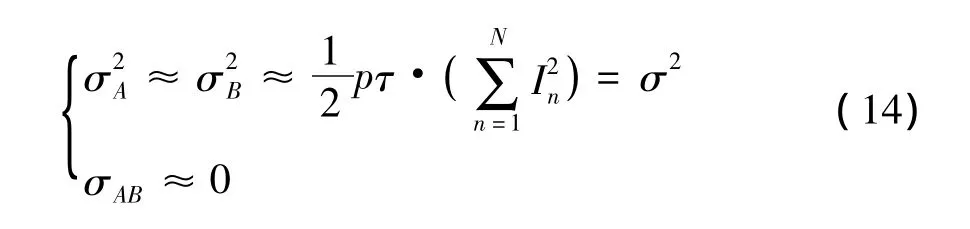
因此在计入误差后方向图的副瓣区域内,A和B组成的联合概率密度函数近似为:

在分析误差造成的影响时,主要关注副瓣区的幅度R的分布情况。
其中R2=A2+B2,做如下假设:

β是副瓣区某方位角上的辐射电平矢量与其实部之间的夹角,α是该方位角误差辐射电平矢量的均值与其实部的均值之间的夹角,并结合(14)式,可得到关于(R和β)的概率密度函数ρ(R,β),如下表达式:
面对“屌丝”流行文化,我们更应该采取的态度是了解、理解、顺应与发展。理解这种文化现象所传达的青年群体的深层需求,顺应青年群体的这种独特表达方式,以发展的视角去更好地回应青年群体的需要。
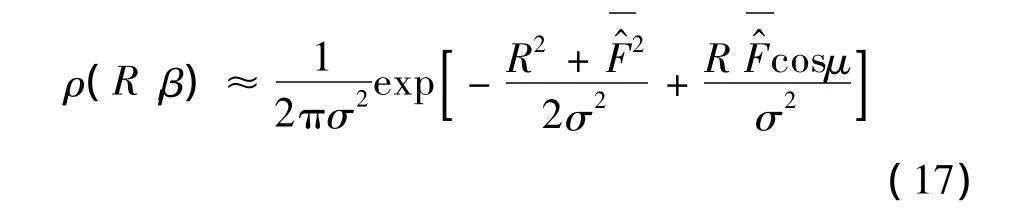
其中μ=β-α,根据文献[3]的数学计算,给出了对上式的化简:
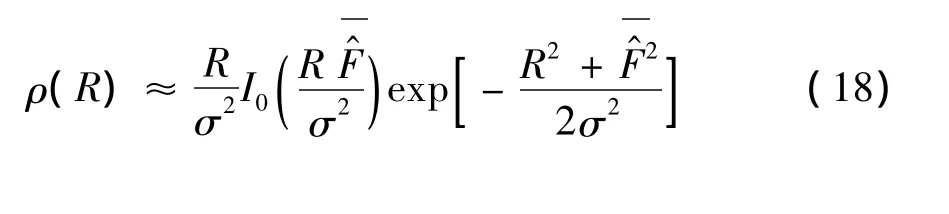

3.3 副瓣区功率电平的概率密度函数及分布函数
一般对副瓣的研究中,我们所关心的是副瓣区的辐射功率电平,在表述过程中也主要以功率电平的分贝值(dB)来衡量天线性能。所以应该对功率电平(dB)的概率密度函数和分布函数进行分析。

线阵模型1:单元数N=100,设计最高副瓣电平为-35dB的 Taylor线阵,其中等电平个数 n-=7,经过万次计算机仿真,统计得到无误差时第一副瓣电平所处方位角上辐射电平的直方图分布,并和理论计算出的该点副瓣电平的概率密度曲线对比,如图2所示。

图2 该方位角辐射电平直方图和其概率密度曲线对比
功率电平与方向性函数的幅度值关系如下:

根据概率论相关理论,有:

对上式两边关于q求导,可得到Q的概率密度函数:

将(17)式带入上式,得到功率电平概率密度函数的最终表达式:

4 误差方向图在某方位角的数值结果
为了论证计算结果的正确性,我们把指定幅、相误差(σΔ=0.05、σΦ=2°)后的某方位角辐射电平分
蓝色直方图是经过计算机万次仿真之后得到该方位角上辐射电平的概率分布,红色曲线是经过(24)式计算得到的该角度上辐射电平的概率分布曲线。可以看出,理论计算和仿真数值结果比较吻合。
由概率密度曲线可以得到计入指定误差后第一副瓣电平的分布函数,如图3所示。
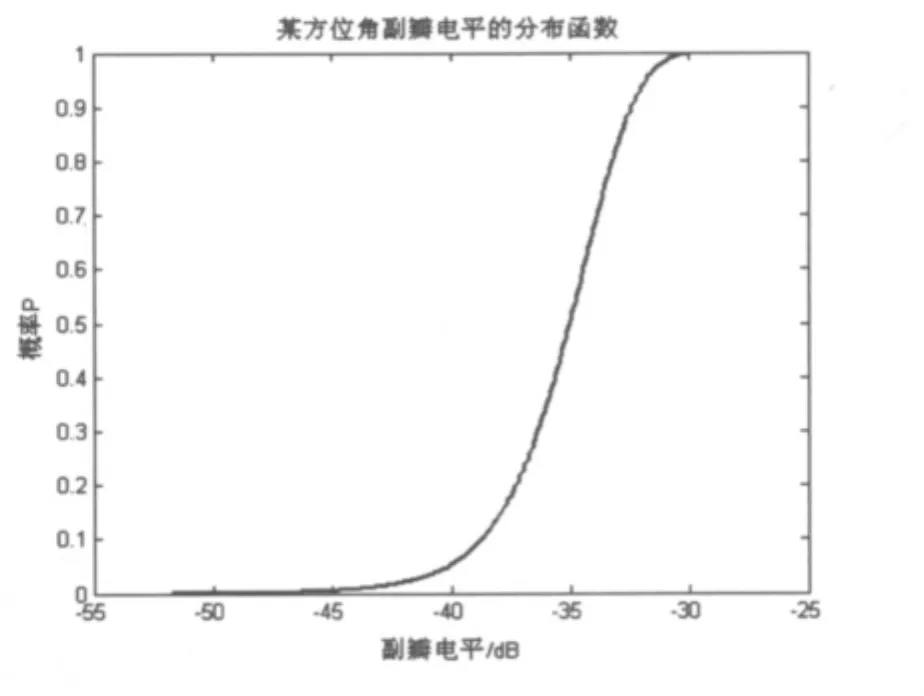
图3 该方位角辐射电平的分布函数
同样以上述线阵模型为例,令总误差σ'2=+,计算得出计入不同误差(σ'=0.02 ~0.09)情况下的分布函数,并作图进行对比说明:

5 误差方向图最高副瓣电平的分析与研究
第4节中的分析都是指定方位角求该点的辐射电平的分布,但在对天线副瓣电平的研究中,我们关心的是最高副瓣的统计规律,求出最高副瓣的概率密度函数或分布函数才是有意义的。
严格意义上,若要求出误差方向图的最高副瓣的统计规律,必须对副瓣区所有点的辐射电平加以分析。
多维随机变量的分布函数可以写成如下表达式:
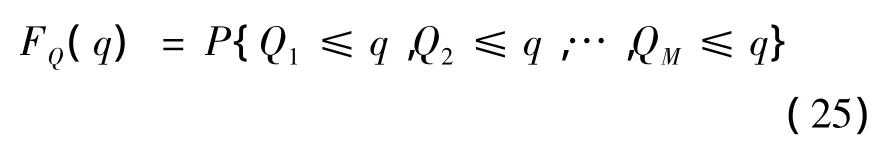
根据(25)式可知,若要求得最高副瓣小于q的概率,则必须得到副瓣区每一个点小于q的概率,最后求所有点的联合分布即就是最高副瓣电平的分布。但实际中这样计算步骤太多,过程比较冗长。所以对此模型进行一个假设,假设如下:
阵列方向图在副瓣区域内,整个副瓣区有M个峰值(M=N-2,N为阵列单元个数)。用小瓣内峰值点辐射电平的概率密度函数来代替计入误差后的小瓣内最高副瓣的概率密度函数(如图5标注所示)。
应用MATLAB对此进行如下论证。采用线阵模型2:单元数 N=100,设计最高副瓣电平为 -35dB的 chebyshev线阵。计入误差(σΔ=0.03、σΦ=2°),经过10000次计算机仿真,首先对小瓣内的峰值点辐射电平的概率密度做一个直方图,如图6所示。之后再仿真得到的整个小瓣内最高副瓣电平分布的直方图,如图7所示。

通过图(6)和图(7)可知,两种情况的概率密度直方图基本吻合。说明当计入的误差不大时,小瓣内峰值点辐射的概率密度分布可以近似代替小瓣最高副瓣的概率密度分布。
应用上面的假设,就可以对整个副瓣区的最高副瓣电平的分布特性进行分析。对于同一个方向图中的各个副瓣电平,显然其数值不是相互独立的;但我们研究的并不是同一个方向图中各个副瓣的统计规律,而是大量的同一类方向图中各方位角的副瓣电平的统计,因此各个方位角上的副瓣电平是近似相互独立的,这样就可以进行如下分析。
由于各方位角上的副瓣相互独立,故(25)式可以变形为:
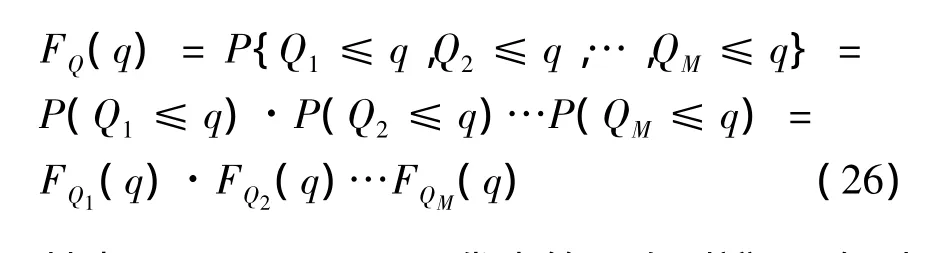
其中Qn(n=1~M)代表第n个副瓣。又有副瓣电平的分布函数是其概率密度函数的积分,得:

将(27)带入(26)就可以求得整个副瓣区最高副瓣电平的分布函数。
同样采用线阵模型2来论证上述分析,计入不同误差,经过10000次计算机仿真。单元数目为N=100,故在整个副瓣区有98个副瓣,结合(27)式,将M=98带入(26)计算得到最高副瓣电平的分布函数并微分求得其概率密度函数,绘制如图中的蓝色曲线。红色直方图是计算机仿真得出的最高副瓣电平的概率密度直方图。
可以看出,不同幅相误差下,计算结果和仿真结果基本吻合,论证了分析过程的正确性。
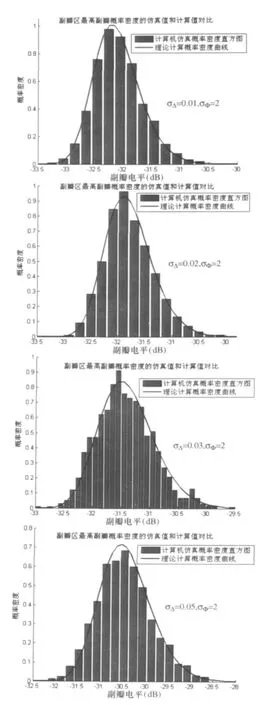
图8 计入不同误差后副瓣区最高副瓣概率密度的仿真值和计算值对比

图9 副瓣区最高副瓣概率密度的仿真值和计算值对比
6 结论
本文在计入随机误差的阵列模型的基础上,运用统计与概率学理论分析了电场方向图副瓣区某方位角上辐射电平的统计特性,之后以副瓣区各方位角的辐射电平分布来分析整个副瓣区的最高副瓣电平的统计特性,并结合计算机仿真验证公式的正确性。
[1]J.K.Hsiao,Effects of Errors on the Sidelobe Level of a Low-Side-Lobe Array Antenna[R].NRL Report,1981.
[2]J.K.Hsiao,Normalized relationship among errors and sidelobe level[J].Radio Science,1984,19(1):292 -302.
[3]J.Ruze,The effect of aperture errors on the antenna radiation pattern[J].Nuovo Cimento,Suppl.3,1952,364 -380.
[4]J.K.Hsiao.Design of error tolerance of a phase array[J].Electronics Letters,1985,21(19):834-836.
[5]S.O.Rice and the theory of random noise:some personal recollections.IEEE transactions on information theory,1988,34(6):1367-1373.
[6]向广志.超低副瓣阵列天线公差分析[J].现代雷达,1996,(12):39 -48.
[7]杨志荣,王建武,傅文斌.互耦和随即幅相误差对直线阵副瓣电平的影响[J].空军雷达学院学报,2008,22(2):94 -96.
[8]谭继兆,沈先军.随机误差对点扫阵列天线副瓣和方向性系数的影响[J].现代电子,2001,(2):25 -32.
[9]汪茂光,吕善伟,刘瑞祥.阵列天线分析与综合[M].北京:电子科技大学出版社,1989,3-19.
[10]高坤,张军.幅相误差对线阵副瓣电平的影响[C].成都:ICCT2012.2012,1030 -1034.
