一种DOA估计的实数特征值分解算法

高青松 周子超 王敏平

(西安电子工程研究所 西安 710100)

1 引言

1986年Schmidt提出 MUSIC 算法[1]，实现了向现代超分辨测向技术的飞跃，也促进了子空间类算法的兴起和发展。MUSIC算法在特定情况下具有很高的分辨力、估计精度及稳定性，因而得到了许多学者的关注和深入研究。ESPRIT算法由Roy等人[2]于1986年提出的，是一种估计信号空间参数的旋转不变技术，利用子阵间的旋转不变技术实现阵列的DOA估计。MUSIC算法和ESPRIT算法一样都需要对阵列接收数据的复数协方差矩阵特征值分解，运算量比较大，当阵元数比较大时，很难满足系统实时性的要求。本文提出一种改进算法，利用Toeplitz矩阵和Hermitian矩阵的性质将复数协方差矩阵转换成实矩阵，避免了复矩阵的特征值分解，减小了运算量，仿真验证了本文提出算法的有效性。

2 算法模型

假定P个窄带远场信号入射到由M个阵元组成的均匀线阵，则阵元接收信号的表达式为:

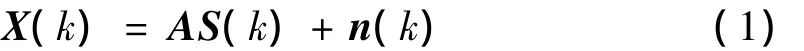
X(k)= [x1(k)，x2(k)，…，xM(k)]T其中，xi(k)为第i个阵元在第k个采样时刻的输出，A=[a(θ1)，a(θ2)，…，a(θP)]为 M × P 维导向矢量阵，a(θi)=[1，e－jφi，e－j2φi，…e－j(M－1)φi]T为 M × 1 维阵列流型矢量，其中φi=(2πd/λ)sin(θi);d为阵元间距;λ为波长;θi为第i个信源的入射角。S(k)= [s1(k)，s2(k)，…，sP(k)]T为 P ×1维空间信号向量，n(k)=[n1(k)，n2(k)，…，nM(k)]T为M × 1维观测噪声向量，ni(k)为均值为0，方差为σ2的高斯白噪声。

3 改进的MUSIC算法分析

由上面的模型我们可以的到数据协方差矩阵

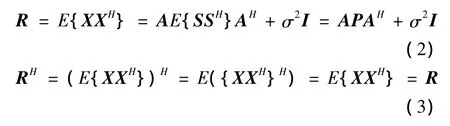
由式(3)知数据协方差矩阵R为Hermitian矩阵[2]，如果我们令 R=Rr+jRi，(Rr、Ri都是实数矩阵)，则

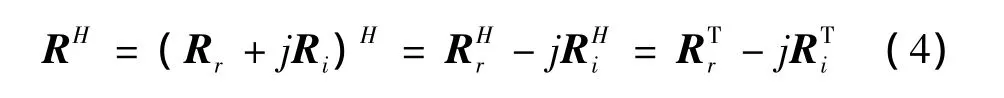
由式(2)、(3)、(4)有

令矩阵R的特征值λk对应的特征向量Wk=

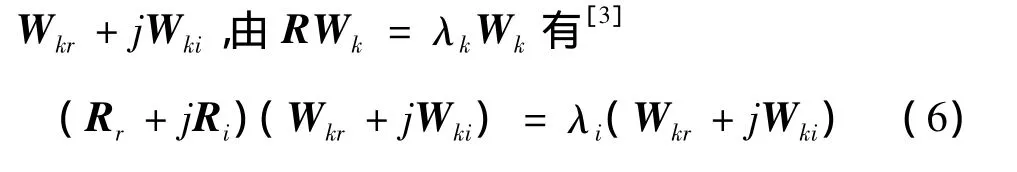
展开后有

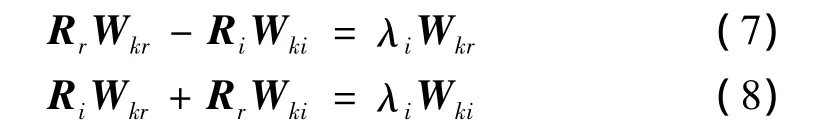
写成分块矩阵的形式有

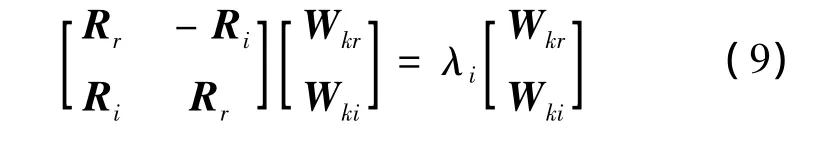
式(5)带入式(9)有

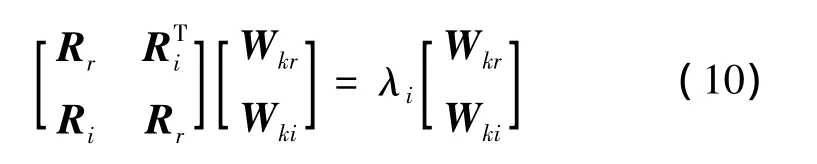
[4]知任何一个2N×2N的实对称Toeplitz矩阵R2N都可以矩阵分块为:

至此，我们得出，将复数协方差矩阵R分为实部Rr和虚部Ri，合成新的实数矩阵T=Rr+JRi，在保持矩阵维数不增加的情况下，通过对矩阵T特征值分解可以精确得到矩阵R的特征值和特征向量，减小了计算量。

另外，由于噪声的影响，使得采样协方差矩阵不是Toeplitz矩阵，如果直接将复数协方差矩阵转换为实数矩阵，其特征值分解误差比对复数协方差矩阵特征值分解误差大。为了进一步减小估计误差，我们可以在得到协方差矩阵后，先对其进行Toeplitz化处理[5，6]，然后再转换为实数矩阵。

下面给出改进MUSIC算法DOA估计的步骤:

给定M个阵元的观测数据x1(t)…xm(t)，t=1，2，…，K。

步骤1 利用观测数据矩阵X=[x(1)，…，x(K)]求自相关矩阵R，(对R进行Toeplitz化处理)，由R=Rr+jRi得到的实部Rr和虚部Ri。

步骤2 构造新的实合成矩阵T=Rr+JRi。

步骤3 对实合成矩阵进行特征值分解T=UΣUH，并确定信源个数p，并存储p个主特征向量u1，…，up或者 M － p个次特征向量 up+1，…，uM。

4 数值仿真及分析

仿真一:均匀线阵，阵元间距d=λ/2，阵元数M=12，入射信号为三个非相干信号，入射角度为[10°，30°，60°]，信噪比相等，都为 SNR=0，采样快拍数为200。仿真比较了常规MUSIC算法和改进MUSIC算法 DOA估计的性能，仿真结果如图1所示。

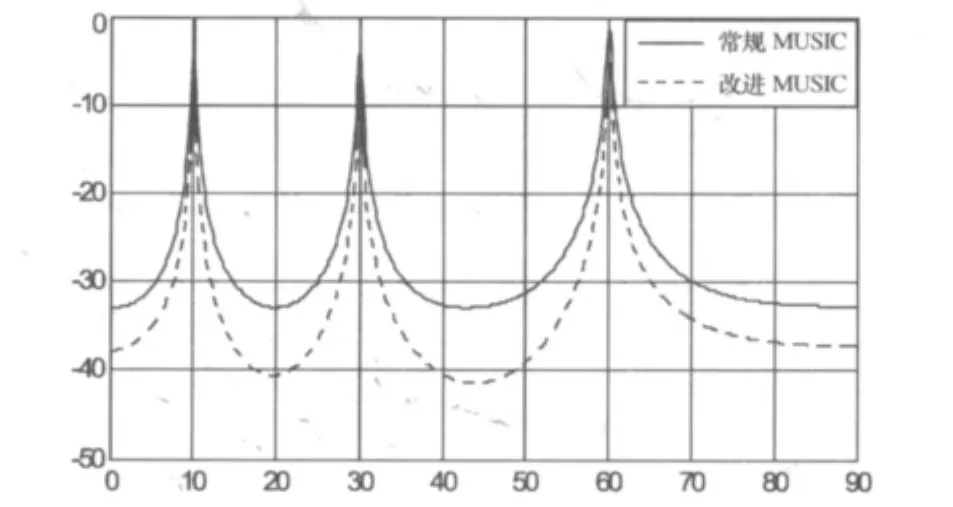
图1 常规的MUSIC法和改进MUSIC法DOA估计

从图1中可以看出，虽然二者都能够准确估计波达方向，但本文提出的算法谱峰更加尖锐，非来波方向的功率更小，更有利于准确估计谱峰的位置。

仿真二:均匀线阵，阵元间距d=λ/2，阵元数M=12，入射信号为三个非相干信号，入射角度分为[10°，30°，60°]，信噪比相等，SNR 从 － 10dB 到20dB，快拍数为300。进行100次独立实验，仿真了MUSIC算法和ESPRIT算法DOA估计的均方误差，仿真结果如图2和图3所示。

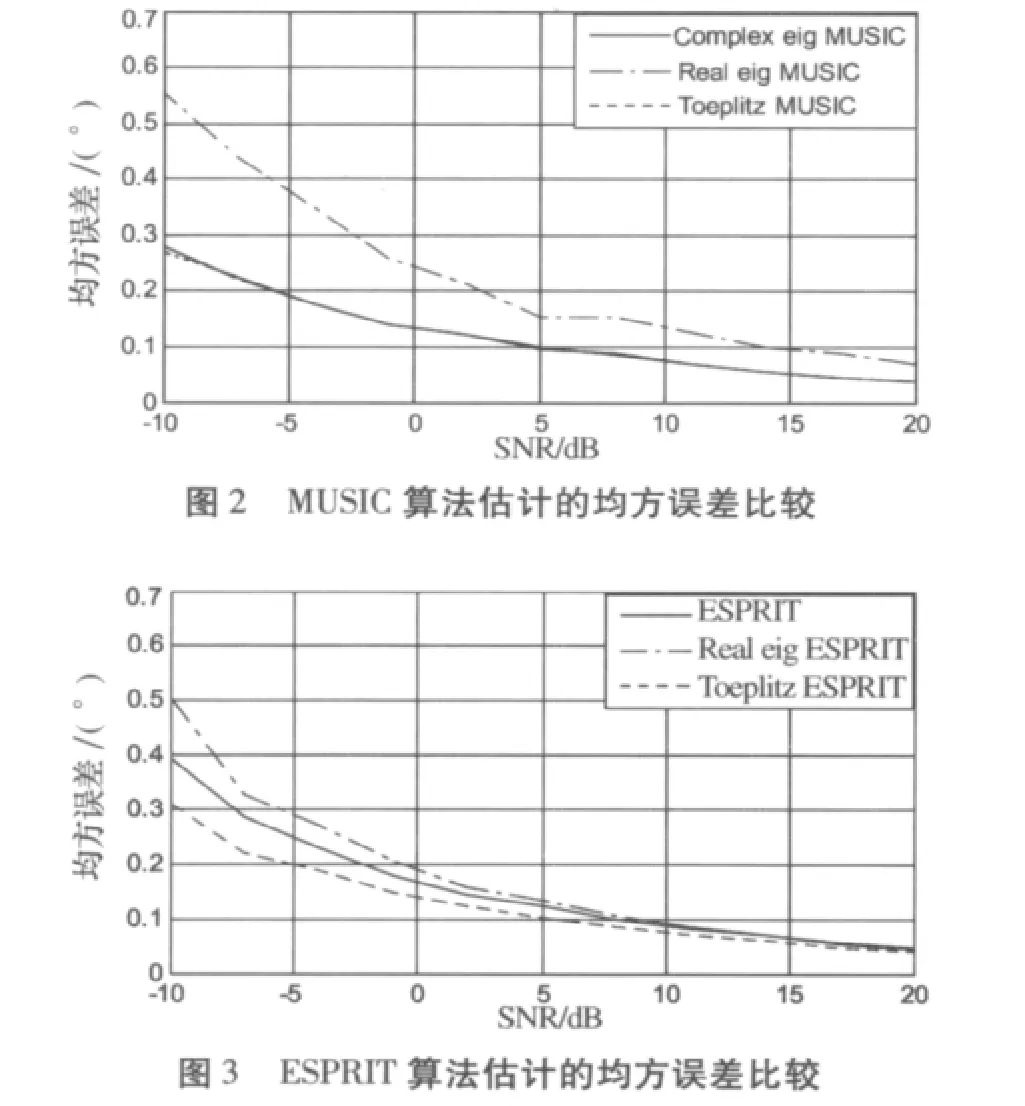
图2中，三条曲线分别为复数协方差矩阵特征值分解常规MUSIC算法、实数协方差矩阵特征值分解MUSIC算法和Toeplitz化复数协方差矩阵，然后转换为实数协方差矩阵特征值分解MUSIC算法的DOA估计均方误差。从图2中我们可以看出，本文提出的实数特征值分解算法的估计均方误差常规MUSIC算法要大，但相差不大，而且随着信噪比增加估计误差趋近相同;此外，我们还可以看出，经过Toeplitz处理的改进MUSIC算法估计的均方误差和MUSIC算法DOA估计的均方误差基本相同，但Toeplitz处理的过程需要增加M×(M－1)次复数加法，在误差要求不十分严格的情况下用改进MUSIC算法即可。

图3中，三条曲线分别为复数协方差矩阵特征值分解常规ESPRIT算法、实数协方差矩阵特征值分解ESPRIT算法和Toeplitz化复数协方差矩阵，然后转换为实数协方差矩阵特征值分解MUSIC算法的DOA估计均方误差。同MUSIC算法类似，实数特征值分解ESPRIT算法的估计均方误差比复数ESPRIT算法的估计均方误差稍大，但Toeplitz处理后估计误差比常规ESPRIT算法小，估计更准确。

5 结论

本文通过将协方差矩阵实部和虚部分离，并合成实数矩阵，对该矩阵进行特征分解可以的到信号协方差矩阵的特征值和特征向量，避免了常规DOA估计算法直接进行复数特征值分解，计算量大的缺点，通过对MUSIC算法和ESPRIT算法进行仿真，验证了本文提出的实数特征值分解算法的有效性。

参考文献:

[1]Schmidt R O.Multiple emitter location and signal parameter estimation[J].IEEE Trans.on Antennas and Propagation.1986:276－280.

[2]Roy R，Paulraj A，Kailath T.ESPRIT－A subspace rotation approach to estimation of parameters of cissoids in noise[J].IEEE Transactions on Acoustics，Speech，and Signal Processing.1986，ASSP －34，(5):1340 －1342.

[3]张贤达.矩阵分析与应用[M].北京:清华大学出版社，2004.

[4]陈洪光，沈振康，郭天天.一种基于PCA分析的DOA估计算法[J].系统工程与电子技术，2005，27(8):1376 －1378.

[5]唐玲，宋弘，陈明举，张江莉.一种基于Toeplitz矩阵重构的相干信源DOA估计算法[J].电子信息对抗技术，2010，25(3):9 －10.

[6]王永良，陈辉，彭应宁，万群.空间谱估计理论与算法[M].北京:清华大学出版社，2004.