集装箱码头间互拖的集卡甩挂运输调度问题

胡 志 华

（1.同济大学经济与管理学院，上海 200092;2.上海海事大学 物流研究中心，上海 201306）

集装箱码头间互拖的集卡甩挂运输调度问题

胡 志 华1，2

（1.同济大学经济与管理学院，上海 200092;2.上海海事大学 物流研究中心，上海 201306）

集装箱码头间的互拖是一种促进相邻码头资源重新组织与优化的协作方式，集装箱甩挂运输能够解耦互拖与港内作业之间的复杂耦合关系。为了提高互拖的集装箱甩挂运输的有效性，满足码头间协调的时间要求和对集卡资源的有效利用，提出了互拖集卡甩挂运输调度的两阶段方法。首先建立互拖任务之间的时间关系网络，然后在此基础上建立集卡调度的混合整数规划模型。算例分析说明了该方法的有效性;演示集卡作业任务序列，分析其码头作业量分布对于港内作业调度的影响。研究结果提供了码头间互拖集卡甩运输的一种参考方法。

互拖;甩挂运输;集装箱运输;车辆路径规划问题;混合整数规划

0 引言

集装箱互拖是已经被上海洋山港2期和3期码头、外高桥1期和2期码头以及其他多个集装箱港口采用的协作策略。通过互拖通道连接两个码头，使得集装箱装卸可以在相邻码头完成，从而拓展了集装箱港口运作优化与协调的范围与空间。港口之间的合作关系历来受到港口企业与学术界的重视［1-3］，而互拖则是相邻码头之间合作的一种具体形式，目前在国内外学术文献中未见研究。然而，现有的模式要求互拖与两码头内部运作之间进行紧密协调，以尽量减少集卡等待时间。由于运输过程和港口装卸作业的复杂性，对运作优化提出挑战。笔者提出基于集装箱甩挂的互拖模式，解耦互拖与码头内部作业的复杂关系。

甩挂运输（truck-and-trailer transport）是指用牵引车拖带挂车至目的地，将挂车甩下后，直接转接新运输任务的运输方式。Gerdessen［4］较早对带挂车的车辆路径问题（Truck and Trailer Routing Problem，简称 TTRP）进行研究。Scheuerer［5］和 Chao［6］使 用 Tabu Search 求 解 TTRP。Lin，等［7-9］采用模拟退火算法研究 TTRP。国内学者包继华，等［10］则从甩挂车辆技术和国内开展甩挂运输的有效性进行论证与分析。对甩挂运输车辆调度的研究，目前文献中非常少见。随着甩挂运输方式的普及，相关的调度、优化和决策问题的研究必将得到重视。

甩挂运输将货物装卸过程与运输过程分离，从而提高牵引车的利用率。这一特点与互拖的结合，使得互拖集装箱运输与集装箱的装卸作业分离，显著降低码头多种作业设备之间的耦合。

1 互拖问题

互拖是集装箱码头，尤其是相邻码头之间充分共享堆场空间、前沿作业空间，以及集装箱作业设施的一种有效方式，逐渐被沿海港口采用。并且在信息技术的支持下，以互拖公共服务平台为纽带，实现协作码头之间作业信息的贡献，从而极大的促进了集装箱港口资源的重调配与再优化。两个相邻码头之间的双港互拖是目前港口企业主要适用的互拖模式，虽然多港互拖理论上具有可行性，但尚未见报道。A和B两个码头之间通过集卡转运集装箱，如图1。通常转运的集装箱是重箱，而空箱转运也可行，只是一般不如重箱紧急。从A码头将集装箱带往B码头后，可能带箱回A码头，抑或空车回。

图1 A、B码头之间集装箱互拖示意Fig.1 Illustration of container mutual transportbetween port A and port B

在不使用甩挂运输的互拖系统中，从A码头将集装箱转运到B码头后，直接卸到B码头堆场，或是等待桥吊或龙门吊等直接对集装箱作业。这种方式又可称为跨港“转堆”。因此，要求精确控制集装箱运输出发和抵达的时间，以减少集卡的等待。为了充分利用桥吊和龙门吊等优先级别更高的港内作业设施，通常牺牲集卡利益，等待难以避免。而甩挂运输则可以充分避免这一点。集卡带箱到B码头，通过控制甩挂装置，直接将集装箱甩到挂车装置上，即可开始新的任务。当B码头能够安排该箱的装卸作业时，再直接调度桥吊和龙门吊等装卸作业设备，或是通过其他甩挂牵引车将该箱带到作业位置。从而将互拖任务完全转化为可控的码头内部作业调度。然而，通过甩挂运输实现互拖的一个问题是，集装箱甩下后采用平堆方式将占用码头空间，在空间非常紧张的码头难以推行。因此，即使采用甩挂，同样要求尽量精确地控制任务的时间窗，以及控制互拖的两个码头的作业量。

2 两阶段方法

2.1 阶段1——生成任务网络

在两个码头之间的互拖运输问题中，所涉及的物流网络简单，仅包括如图1的A和B两个码头，以及在A和B之间的双向互拖通道。互拖的关键是尽量降低集装箱在目的港的堆放时间，最佳策略是直接通过桥吊装船。如果是进口箱则直接由外集卡到集装箱所在码头取箱，避免再次中转。根据互拖集装箱在两个码头的时间约束，建立互拖任务之间的优先关系图，即任务网络。

2.1.1 集合与参数

1）N={2，3，…，NJ+1}:任务集合。

2）TL:两个码头之间的运输时间。

3）TP:集装箱运输到目的港后，仅完成甩挂所需作业时间。

4）Fn∈{0，1}:如果任务n∈N是从A码头运输到B码头，则为0;否则为1。

5）［Ij，IIj］:任务j∈N的时间窗口，显然应当满足IIj-Ij≥TL+2TP。

2.1.2 虚拟任务

定义两个虚拟任务:开始任务1和结束任务（NJ+2），加入集合J得到V=N∪{1，NJ+2}。

起止两个虚拟任务的时间窗通过下面的规则定义:

1）定义为［L，U］∶［L1，U1］=［LNJ+2，UNJ+2］=［minj∈NIj，maxj∈JIIj］;

2）∀n∈N，［Ln，Un］=［In，IIn］

在集合N之上，定义参数A和T分别表示任务图连接矩阵和运输时间矩阵。

2.1.3 计算任务之间的时间矩阵

如果任务i∈V和j∈V由同一集卡相继服务，任务之间由于场地变换的时间定义为Ti，j。对于虚拟开始任务，能够紧接着对任意任务进行服务;对于虚拟结束任务则可以在任意任务结束后执行;另外，如果第1个任务是从A到B，而第2个任务是从B到A，则依次对两个任务服务的时间间隔都定义为0。如果从第1个任务最早时间开始，经过源港装卸、运输、目的港装卸之后，能够赶上第2个任务的最晚开始时间，则两个任务之间的连接时间是TL。在以上情况之外，T=∞。即，矩阵T通过式（1）定义:

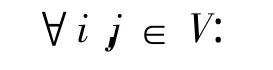
通过以上定义得到任务集合V、任务时间窗口［Li，Ui］、任务之间的时间矩阵T和连接矩阵A。

2.2 阶段2——集卡甩挂调度

第2阶段集卡甩挂调度的关键是确定集卡的作业序列。

2.2.1 集 合

1）V={1，2，…，NJ，NJ+1，NJ+2}:其中，1 和（NJ+2）为虚拟起止节点。

2）K={1，2，…，NK}:即集卡牵引车集合。2.2.2 参 数

1）Di:任务∀i∈V需要的容量，由于采用集卡单元化运输，则∀i∈N，Di=1，且D1=DNJ+2=0，从完整角度看该参数能够处理带有多挂车的运输任务。

2）Pi:任务∀i∈V的处理时间，∀i∈N，Pi=TL+2TP，且P1=PNJ+2=0。

3）Ti，j，∀i∈V，j∈V:在第1 阶段定义的任务时间矩阵。

4）Ai，j，∀i∈V，j∈V:在第1 阶段定义的任务连接矩阵。

5）M:一个足够大的数，主要用于转换非线性表达式。

6）DP1=1，DP2=NJ+2:表示起止两个虚拟任务。

7）CAP:集卡线路上任务数量限制。

2.2.3 决策变量

1）xk，i，j∈{0，1}:x是流变量，如果车辆k∈K在服务完任务i∈V后紧接着服务任务j∈V，则为xk，i，j=1;否则为 0。

2）τk，i:车辆k∈K对任务i∈V开始服务的时间。

2.2.4 目标函数目标是总服务时间的最小化，如式（3）:

2.1.4 计算任务连接矩阵

任务连接矩阵是0/1矩阵，1表示两个任务之间可以直接相继为同一集卡作业;0则表示不可行，如式（2）:

2.2.5 约束函数

虚拟任务之外的其他任何任务都仅需要被服务1次，如式（4）:

对于任意集卡，从虚拟开始节点出发，到虚拟结束节点后完成运输，仅负责一个任务序列，约束如式（5）和式（6）:

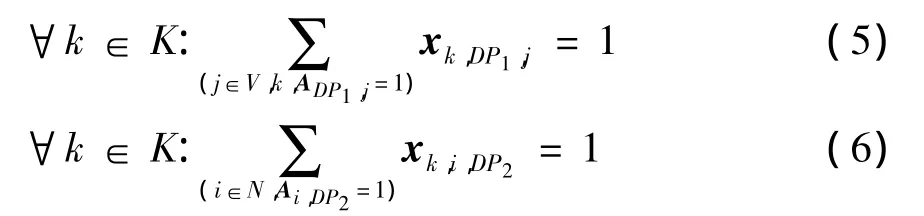
对任意集卡，对任意非虚拟任务，满足该任务在任务网络中的流约束，如式（7）:

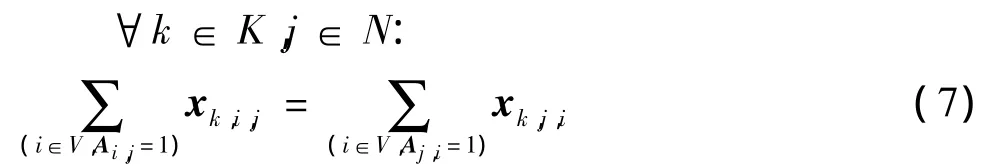
对任意集卡负责的线路，即该线路上的任务序列，通过相继关系x及相应时间序关系t规避线路上的子回路，式（8）是一个非线性表达式:

式（8）通过式（9）转化为一个线性表达式，从而使得最终建立的模型是0/1整数规划模型:

根据式（10）和式（11）建立时间窗约束:

根据式（12）建立集卡线路的工作量约束，在满足其他约束和最小化服务时间的前提下可以通过该参数均衡各个集卡的工作量:

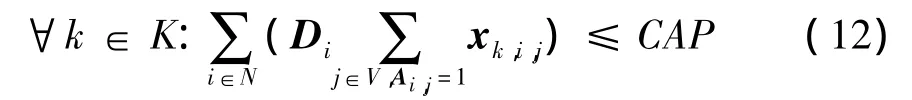
通过目标函数式（3），约束函数式（4）～式（7），式（9）～式（12）定义了集卡甩挂任务调度的0/1整数规划模型。

3 算例分析

以上海洋山港2期和3期码头之间，以及外高桥1期和2期码头之间的互拖通道为例，验证文中提出的两阶段方法。取TL=15，TP=2，CAP=20。20个互拖任务及其时间窗和转运方向见表1。其中，虚拟任务1和22分别表示起止任务节点，时间窗取［0，240］，即20是个互拖任务要在一个4 h的小工班内完成，它们的时间窗配置也正是说明这一点。然后，根据式（1）计算任务之间的时间矩阵T。根据式（2），计算任务之间的连接矩阵A。

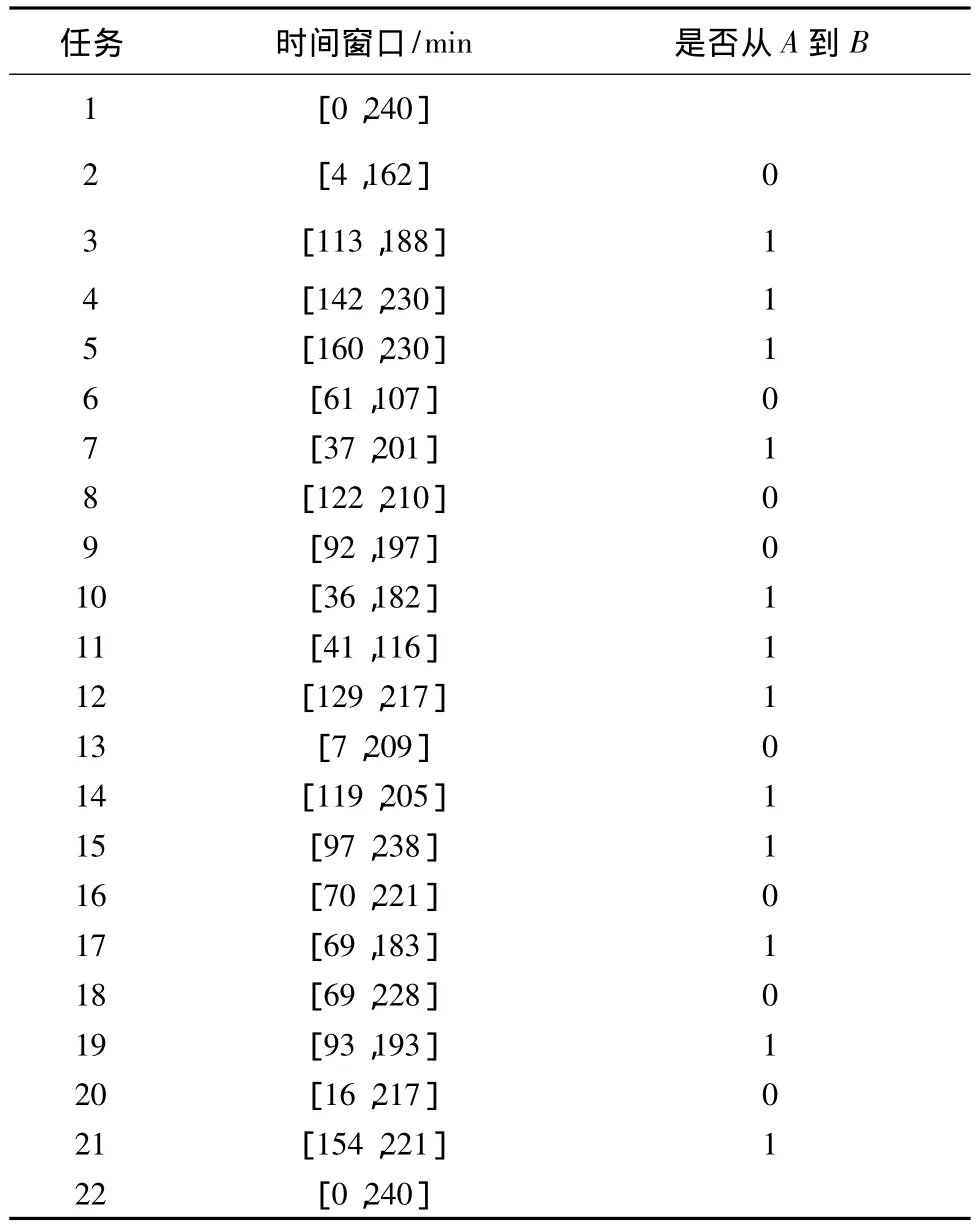
表1 互拖任务及其时间窗与转运方向Table 1 Mutual transport tasks，time windows and transport directions

采用Gurobi 4.6对2.2节建立的混合整数规划模型进行求解，经过0.01 s左右计算，得目标函数为338。因而3条线路及其依次服务的任务如下:①11，13，3，2，5;②7，6，10，9，14，19，16，12;③17，8，4，20，21，18，15。

3条线路分别完成5，8和7个任务。通过调整参数，设置CAP=7，通过0.01 s左右的计算得到结果，目标函数值依然是338。3条线路如下:①11，20，4，13，3，16，21;②19，2，15，9，10，8，5;③7，6，14，17，18。

综合3条线路，线服务的任务序列，以及各个任务的时间窗口与分派的开始作业时间，如表2，最后的任务方向表明互拖任务是从哪一个码头转运到另一个码头。

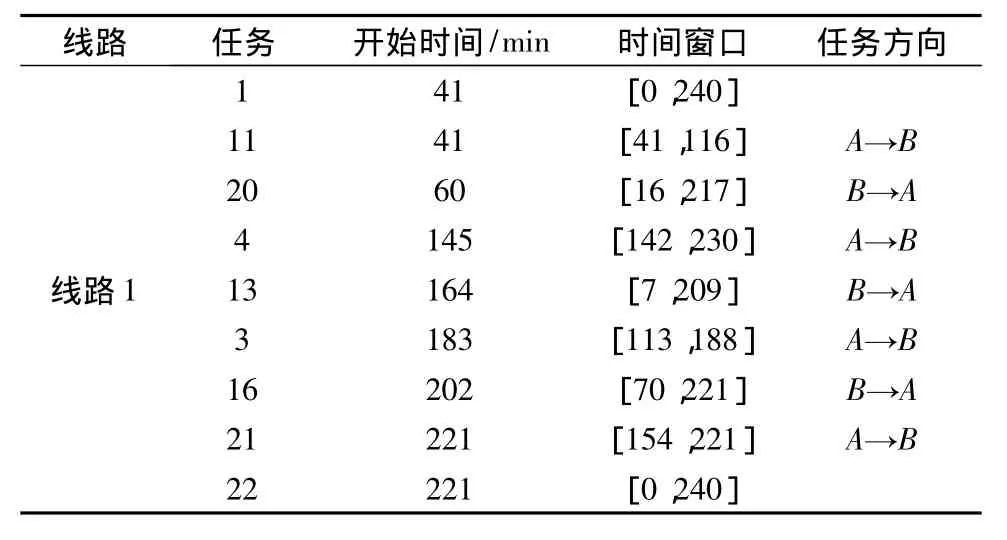
表2 线路任务排序及其开始时间与时间窗口Table 2 Task sequences，the starting time and time windows

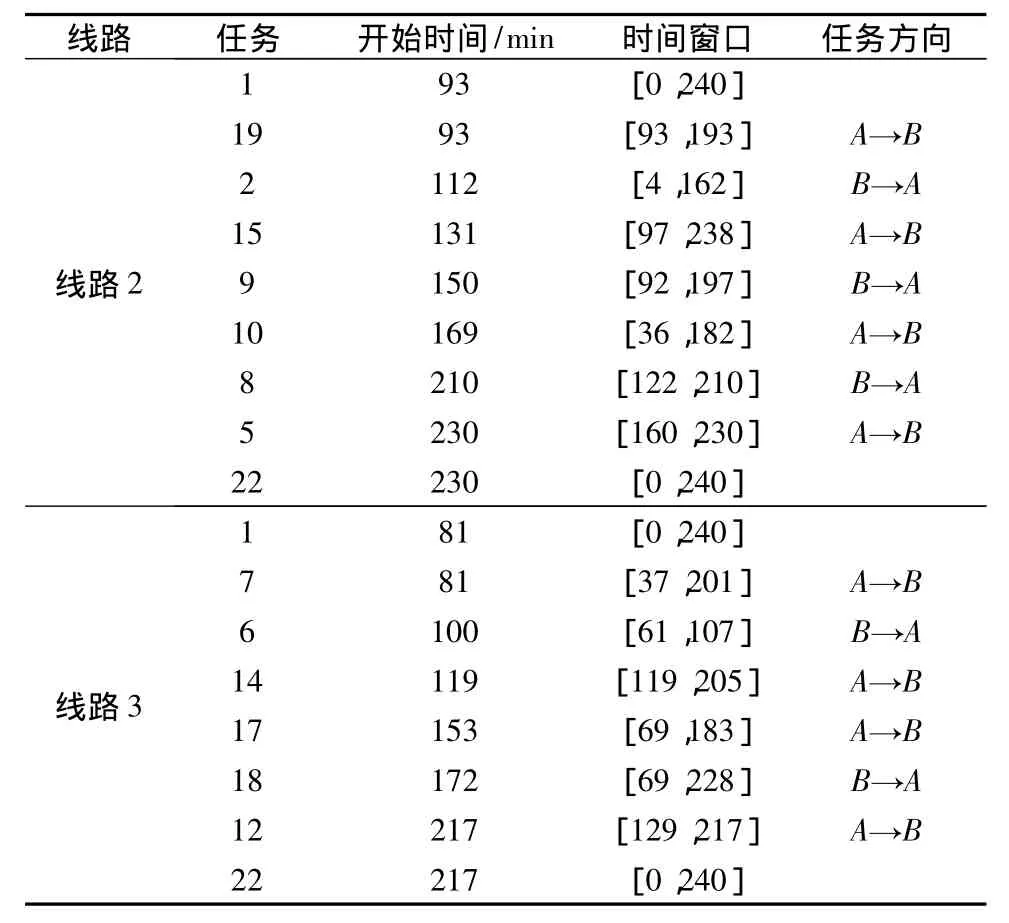
（续表2）

图2为根据表2的信息，直观地说明了3个任务序列在两个码头之间的集装箱转运过程。3种不同线型分别表示3个任务序列。从图中可以看出，有些折线相互并没有连接在一起，则表明相继的任务之间集卡有等待时间。

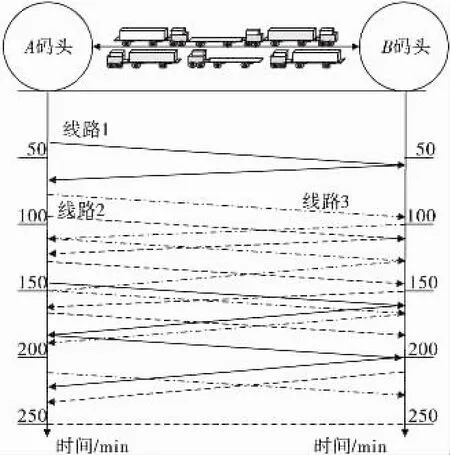
图2 两个码头之间的互拖线路安排Fig.2 Routing between two ports for container mutual transport

根据表2和图2的信息，通过将作业工班划分为5个区间，每个区间50 min，通过每个区间内A和B两个码头的作业量，得到作业量分布如图3。

图3 码头装卸作业量分布Fig.3 Workload distribution of container loading and unloading in ports

从图3可以看出，由于是独立的一个工班，没有前后的滚动任务，因此在首部时段作业量较少;而后的4个时段作业量基本均衡;从两个码头各个时段的作业量来看，也非常均衡，其中主要的一个原因是两港之间的转运时间与甩挂时间之和在15～19之间，完全在一个时间区间之内。图3的另一个更重要的目的是为两个码头的装卸搬运调度服务。通过该直方图能够获得不同时段对桥吊、龙门吊或正面吊等其他集装箱作业资源的需求。另一方面，该直方图也能够反过来约束集卡甩挂的调度，通过建立资源约束的甩挂调度模型使得不同时段满足不同的资源限制。

4 结语

通过对双港互拖问题的研究，提出基于集装箱甩挂运输的互拖方法以解耦互拖与集装箱港口内部作业调度之间的复杂关系。建立了两个码头之间集装箱互拖甩挂运输调度的混合整数规划模型，通过算例验证模型的有效性。下一步的研究方向包括:大规模甩挂调度的有效调度策略与算法;考虑软时间窗口和运输时间不确定性的集卡甩挂调度;多港协调的集卡甩挂资源配置与调度;集卡甩挂与码头内作业的协调优化。

（References）:

［1］ 张欣，施欣.基于合作对策的江苏沿江港口合作竞争研究［J］.中国航海，2007（3）:69-72.

Zhang Xin，Shi Xin.Research on co-competition among ports along the Yangtze river in Jiangsu province based on cooperative game model［J］.Navigation of China，2007（3）:69-72.

［2］ 周鑫，沙梅，郑士源，等.基于空间区位模型的港口企业合作定价策略［J］.上海交通大学学报，2011，45（1）:125-129.

Zhou Xin，Sha Mei，Zheng Shiyuan，et al.Pricing strategy of port enterprises under cooperation condition based on located spatial model［J］.Journal of Shanghai Jiaotong University，2011，45（1）:125-129.

［3］ 庄佩君.集装箱港口竞合战略研究［J］.中国航海，2005（1）:77-81.

Zhuang Peijun.Co-opetition:A new strategy for container ports［J］.Navigation of China，2005（1）:77-81.

［4］ Gerdessen J C.Vehicle routing problem with trailers［J］.European Journal of Operational Research，1996，93（1）:135-147.

［5］ Scheuerer S.A tabu search heuristic for the truck and trailer routing problem［J］.Computers and Operations Research，2006，33（4）:894-909.

［6］ Chao I M.A tabu search method for the truck and trailer routing problem［J］.Computers and Operations Research，2002，29（1）:33-51.

［7］ Lin S W，Yu V F，Chou S Y.Solving the truck and trailer routing problem based on a simulated annealing heuristic［J］.Computers and Operations Research，2009，36（5）:1683-1692.

［8］ Lin S W，Yu V F，Chou S Y.A note on the truck and trailer routing problem ［J］.Expert Systems with Applications，2010，37（1）:899-903.

［9］ Lin S W，Yu V F，Lu C C.A simulated annealing heuristic for the truck and trailer routing problem with time windows［J］.Expert Systems with Applications，2011，38（12）:15244-15252.

［10］包继华，张鑫，张建武.一种新的汽车列车动力学建模方法［J］.上海交通大学学报，2007，41（2）:244-249.

Bao Jihua，Zhang Xin，Zhang Jianwu.A new method of dynamic model building of combination vehicles［J］.Journal of Shanghai Jiaotong University，2007，41（2）:244-249.

Scheduling of Container Truck-and-Trailer Transport between Two Ports

Hu Zhihua1，2
（1.School of Economics＆ Management，Tongji University，Shanghai 200092，China;
2.Logistics Research Center，Shanghai Maritime University，Shanghai 201306，China）

Mutual transport among container ports cooperatively enhances the reorganization and re-optimization of operational resources among neighboring ports.In order to enhance the validity of mutual transport by container truck-and-trailer transport，and to satisfy the time constraints，a two-stage approach is proposed for scheduling container trucks for mutual transport.First，a time relationship matrix is built among mutual transport tasks;second，a mixed integer linear programming model is built for container trucks.Numeric samples are employed to show the validity of the approach，and demonstrate the sequences of the tasks for trucks.Moreover，the influences of distribution of mutual transport tasks to operations scheduling within ports are analyzed.The result provides a reference approach for scheduling truck-and-trailer container trucks for biport mutual transport.

container mutual transport;truck-and-trailer transport;container transport;vehicle routing problem;mixed integer linear programming

F253.4

A

1674-0696（2013）02-0313-05

10.3969/j.issn.1674-0696.2013.02.30

2012-05-11;

2012-09-05

国家自然科学基金项目（71101088，71171129）;社会科学基金重大项目（11＆ZD169）;中国博士后科学基金项目（2011M500077，2012T50442）;教育部人文社科一般项目（10YJC630087）;教育部博士点基金项目（20113121120002）;上海市自然科学基金项目（10ZR1413200，10190502500，11510501900）;上海市教委项目（11YZ137）

胡志华（1977—），男，湖南长沙人，博士，主要从事港航与物流运作优化、社会科学计算实验与计算智能方面的工作。E-mail:zhhu@shmtu.edu.cn。