一种运输作业指派的迭代下降组合拍卖机制设计

李莉英

（重庆交通大学理学院，重庆 400074）

一种运输作业指派的迭代下降组合拍卖机制设计

李莉英

（重庆交通大学理学院，重庆 400074）

针对4PL公司的卡车运输作业指派问题提出了一种基于内生投标的迭代下降组合拍卖机制设计。根据获胜者确定问题，构造出一个限制对偶规划，其最优解提供近似单条线路运输作业的价格信息。投标者（3PL企业）根据这些价格信息，在近视最佳反应投标策略下能够确定新的有利可图的线路组合，并以此进行下一轮的投标。数值试验显示，基于内生投标的迭代拍卖机制与基于外生投标的迭代拍卖机制相比具有更高的指派效率。

运输作业指派;迭代组合拍卖;近视最佳反应投标策略;内生投标

0 引言

随着市场竞争的日益加剧和企业对物流服务深层次性和全面性要求的提高，传统的第3方物流（3PL）企业由于缺乏运作整个供应链的能力而逐渐不能满足企业的物流需求，因而第4方物流（4PL）作为供应链集成商应运而生。4PL公司通过其物流信息平台，一方面可以接受多个运输作业，另一方面能够找到多个3PL企业。于是，探讨4PL公司如何将接受来的运输作业有效地指派给合适的3PL企业，使得整个服务成本最小化，这在管理实践中有着重要意义。

在国外，许多大公司购买运输服务〔特别是卡车运输服务（TL）〕基本上都是通过参加投标过程来进行的，产生的合同价格在1～2a内有效。卡车运输服务的特点是3PL企业在一些不规则的路线上运作，即从某个发点到某个收点做整车直达运送，中间无任何停留。运输服务的采购投标过程与一般商品的采购投标过程有许多相同的特征。然而，在某些方面有些不同。其中，最不同的就是运输成本受范围经济影响的程度大于受规模经济影响的程度。3PL企业的收益不仅仅依赖于单个运输作业的价格，更重要的是中标的各个作业能否与3PL企业整个运输网络中正在运作的其它运输作业联系起来，从而最大化装备（卡车）和司机的利用率，使得整个运输成本尽可能地减少。正因为这个原因，运输服务拍卖主要采用组合拍卖的方式［1-5］。也就是，3PL企业可以将一些相关性较强的线路运输作业进行组合投标，以便充分平衡其运输网络需求，发挥网络的协同效应，达到降低总服务成本的目的。而且，采购商（4PL公司）也会提高讨价还价能力，从而降低总的采购成本。因此，通过组合拍卖来采购运输服务，可以同时降低采购商和3PL企业双方的服务交易成本，达到物流系统整体优化的目的。

自从Caplice首次将组合拍卖引入运输服务采购领域，提出各种承运人指派模型以来，运输服务组合拍卖问题越来越受到人们的关注［1］。Ledyard，等［2］验证了组合拍卖给托运人带来的收益，西尔斯物流公司在1993年所做的卡车运输服务采购，由于组合拍卖的使用，为西尔斯物流公司每年带来近1.65亿美元的成本节省。Song，等［3］根据一组模拟数据主要从承运人角度检查了组合拍卖带来的成本节省。Y.Sheffi［4］对组合拍卖在运输服务采购中的适用情况作了调研，特别是如何将服务水平和其他非价格因素融合到组合拍卖的框架中去进行了说明，为使用采购运输服务的公司提供了较全面的决策支持。A.Lim，等［5］研究了一个运输需求量随季节变化的运输采购模型，其中托运人为承运人在非高峰时期的运送提供运量保证，该文作者采用分解启发式方法对拍卖模型进行了求解。杨华龙，等［6］以运价、服务质量、信誉和网络覆盖等因素为衡量标准，构建了一个集装箱航运服务的多属性组合拍卖模型。

以上学者虽然成功地将组合拍卖引入到运输服务采购领域，但是在拍卖机制设计方面，不管使用的是单轮拍卖还是多轮拍卖，他们都假定投标者在拍卖之前明确知道自己想要投标的组合。然而，所有可能的允许组合数目呈指数次幂，一个投标者要对所有允许组合定价并从中选择有限多个进行投标，这往往是很困难的。此外，拍卖者在组合拍卖中需要求解的获胜者确定问题（WDP）是 NP完全问题［7］。Parkes，等［8］指出，当投标者难以确定所要投标的组合的价值时，迭代组合拍卖方式能够减轻这种负担。在迭代组合拍卖机制中，投标者能够根据价格信息做出反应，从而调整投标策略。Kwon，等［9］提出，内生投标机制能使投标者在拍卖过程中根据单物品的价格信息不断找出新的有价值的组合，而且拍卖者在每一轮求解的WDP的规模小于一般组合拍卖中WDP的规模。这样，既避免了投标者事先列举所有允许组合的麻烦，同时也能提高物品的分配效率。这种基于单物品价格信息的拍卖机制类似于资源分配设计（RAD）机制中基于市场的优化方法［10］。

笔者针对4PL公司的卡车运输作业指派问题的特点，提出基于内生投标的迭代下降组合拍卖机制设计，与原有关于卡车运输服务组合拍卖的文献相比，具有以下特点:①在多轮迭代拍卖的背景下，构造出单条线路的近似价格，并利用这些价格对线路组合进行定价;②在内生投标拍卖机制中，给出了投标者的具体要求报价形式。由于内生投标机制既能保持组合价格下降的性质，又能保持投标者的近视最佳反应的性质，而有效迭代拍卖机制的所有其它规则保持不变，因此本拍卖机制在拍卖结束时能实现系统的最优指派。

首先介绍针对运输作业指派的一般（基于外生投标）迭代组合下降采购拍卖机制的实施规则，稍后提出的基于内生投标的迭代下降组合拍卖机制将以它作为基础。

1 迭代下降组合采购拍卖规则

组合采购拍卖的迭代机制包括投标形式和投标要求报价、获胜者确定规则、近视最佳反应投标策略和拍卖结束规则等方面的内容。它们的共同作用使得拍卖者的所有运输作业实现最优的指派。下面具体介绍相关规则。

1.1 投标形式和投标要求报价

基于运输作业采购拍卖的实际情况，允许投标者对多个不相交的运输作业组合进行累或（OR）投标，即如果一个OR投标形式为{S1，S2}，则投标者希望能中标组合S1中的全部运输作业，或者中标组合S2中的全部运输作业，或者同时中标组合S1和S2中的全部运输作业。它和异或（XOR）投标［8］是不一样的，一个XOR投标不允许投标者同时中标两个以上的组合。本拍卖中，在第t轮对组合S的要求报价表示为（S），投标者j对组合S的实际报价表示为（S）。投标者j在第t轮对组合S的实际报价（S）必须等于或低于要求报价（S），并且至少低出ε，ε为本拍卖的最小投标减少量。如果某个投标者在第t-1轮是组合S的暂时获胜者，则对其在第t轮的要求报价等于其在上一轮的获胜投标价，即。如果某个投标者在第

t-1轮不是组合S的暂时获胜者，则对其在第t轮的要求报价等于第t-1轮不中标者的最低投标价减去ε，即:

式中:unhappy代表在第t-1轮中未中标的投标者。

在拍卖的第1轮，无要求报价，各投标者可以对预先决定的组合进行初始报价。

1.2 获胜者确定规则

在拍卖的每一轮结束之后，拍卖者需要计算一次获胜者确定问题（WDP），以便明确当前的暂时获胜者，其优化目标是使总的采购成本最小化。WDP的约束条件是:每一条线路的运输作业不重复拍卖，即最终只中标且只能中标1次。笔者假定投标者的人数足够多，使得WDP基本上总有最优解，这一点通过4PL公司的网络信息平台是可以做到的。当WDP的最优解有多个时，选取获胜者人数最多的最优解;如果多个最优解的获胜者人数相同，则随机选取1个最优解。当拍卖结束时，该轮的暂时获胜者就是最终获胜者。

1.3 近视最佳反应投标策略

本拍卖假定投标者都是采用近视最佳反应投标策略，即其投标行为都是基于当前轮次效用最大化来考虑的。具体来说就是，在拍卖的任意一轮中，给定组合的要求报价，投标者j会选取优化问题BIP的最优解所确定的运输作业组合进行投标，BIP的目标函数是最大化投标者j的拟线性效用。

1.4 拍卖结束规则

拍卖在下述两种情况之一发生时即可结束［8］:

1）当所有投标者在连续两轮的投标中都递交了相同的投标。该条件表示所有投标者已经到了投标个体理性的边界，拍卖者的采购成本不能再进一步减少。

2）当所有投标者都是获胜者，即每一个投标者都得到她所投标的所有组合。该条件表示此时的指派结果已经不能再改进系统的优化目标。

上述拍卖机制的有效性由下列性质给出。

性质 假定各投标者采用近视最佳反应投标策略，则本拍卖模型在拍卖结束时能够实现系统的最优指派（当投标减量足够小时）。

性质的证明类似于文献［8］中应用原-对偶算法来解释迭代组合上升拍卖机制的有效性，故此略去。该性质说明，在拍卖结束时组合价格逼近竞争均衡价格，此时各投标者的效用达到渐近最大化，同时拍卖者的采购成本达到渐近最小化。

2 模型描述

假设一个4PL公司（拍卖者）要把n条不同线路的卡车运输作业指派给m个潜在的3PL企业（投标者）。n条不同线路的运输作业构成的集合记为I，即|I|=n。m个潜在的3PL企业构成的集合记为J，即|J|=m。拍卖者允许投标者根据自己的运输网络需求将部分线路的运输作业进行组合投标，这样的允许投标组合（捆绑）记为S，S⊆I。

假定3PL企业j（j∈J）对组合S具有私人的拟线性效用uj（S）=Pj（S）-cj（S），其中cj（S）表示3PL企业j服务组合S的私有成本，而Pj（S）表示3PL企业j对组合S的报价。投标者j为了确定向哪些线路组合进行投标，需求解下列整数规划问题（BIP）:

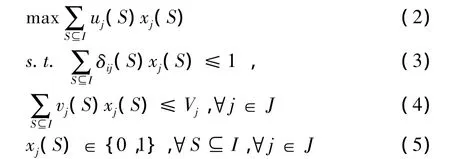
式中:xj（S）为0-1变量，表示投标者j对组合S是否进行投标;δij（S）表示投标者j所构建的线路组合S是否包含线路i，若包含，则 δij（S）=1，否则，δij（S）=0;vj（S）表示服务组合S时投标者j需要的运输能力;Vj表示投标者j当前拥有的最大运力。

式（2）为目标函数，表示最大化投标者j的效用值;约束（3）表示投标者j要投标的各组合之间不相交，即不包含相同线路的运输作业;约束（4）表示投标者j要投标的所有线路组合中需要的运力不超过其最大运力。

当每一个投标者都递交了使其效用最大化的线路组合以后，拍卖者（4PL公司）需要考虑将运输作业如何有效地指派给投标者，使得其总的采购成本最小化。于是，拍卖者需要求解下列获胜者确定问题（WDP）:

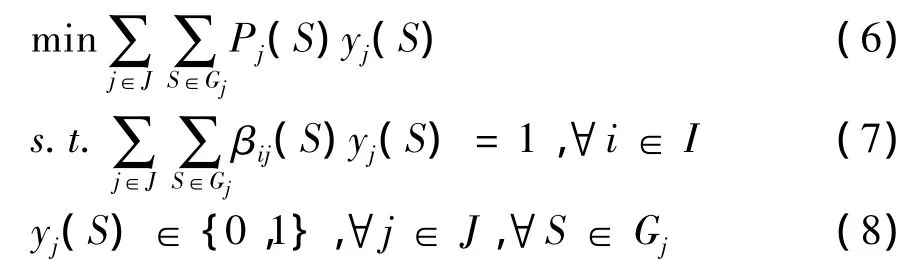
式中:yj（S）为0-1变量，表示投标者j向拍卖者提交的组合S是否中标;Gj表示投标者j根据效用最大化提交的线路组合所构成的集合;pj（S）表示投标者j对组合S的报价;βij（S）表示投标者j所提交的线路组合S是否包含线路i，若包含，则βij（S）=1，否则，βij（S）=0。

式（6）为WDP的目标函数，表示最小化拍卖者的总采购成本;约束（7）表示对于集合I中每一条线路的运输作业不重复拍卖，即最终只中标且只能中标一次。

根据基于外生投标的迭代组合采购拍卖机制，拍卖者通过求解WDP就可以实现所有运输作业在3PL企业之间的暂时指派（如果WDP有最优解的话）。然后，拍卖者宣布获得暂时指派的投标者及其投标价格。投标者根据这些价格信息做出反应，即调整下一轮的投标策略。如此反复进行下去，直到满足拍卖结束的条件，则能实现4PL公司的作业在3PL企业之间的最终指派。

基于外生投标的迭代组合采购拍卖机制实际上假定投标者在拍卖之前明确知道自己想要投标的组合，即他能详细列举并定价所有可能的允许组合。正如引言中所说，这往往是很困难的，尤其是当拍卖的运输作业数n很大时。

3 内生投标机制与单条线路运输作业定价

内生投标的基本思想是在多轮拍卖过程中投标者可以不断提交新的有利可图的线路组合。利用单条线路的运输作业服务价格，投标者能够对拍卖开始之前未曾考虑的线路组合进行定价和投标。

3.1 近似单条线路运输作业定价

笔者对单条线路运输作业的服务价格做如下两个假设:

1）在拍卖的任意一轮中，对于已经获得暂时指派的组合来说，它所包含的各单条线路运输作业的服务价格加起来应等于暂时获胜者的投标价格。

2）在拍卖的任意一轮中，对于暂时未获得指派的组合来说，它所包含的各单条线路运输作业的服务价格加起来应小于或等于不中标的最小投标价格。

为了使得迭代拍卖的下降性质得以保持，上述两个假设是必要的。如果假设1）不成立，例如，对于已经获得暂时指派的组合来说，如果各单条线路运输作业的服务价格之和大于暂时获胜者的投标价格，则那些未中标的投标者在下一轮将以单条线路运输作业的服务价格之和投相同的标。然而，这样的投标将是无效的。因为按照迭代下降的拍卖性质，作为暂时未获得指派的投标者来说，下一轮的投标价格至多为本轮不中标的最低投标价减去ε。如果各单条线路运输作业的服务价格之和小于暂时获胜者的投标价格，这将会使得一些成本更低的投标者失去获得分配该组合的机会。如果假设2）不成立，则在下一轮投标中，那些未中标的投标者将以单条线路运输作业的服务价格之和投标相同的组合，由于导致更高的效用，该组合仍属于其最佳反应集中的元素，按照迭代下降的拍卖性质这样的投标仍然是无效的。

下面构造满足上面两个假设条件的单条线路运输作业的服务价格。

WDP的线性松弛问题（LP）为:

LP的对偶问题（DP）如下:

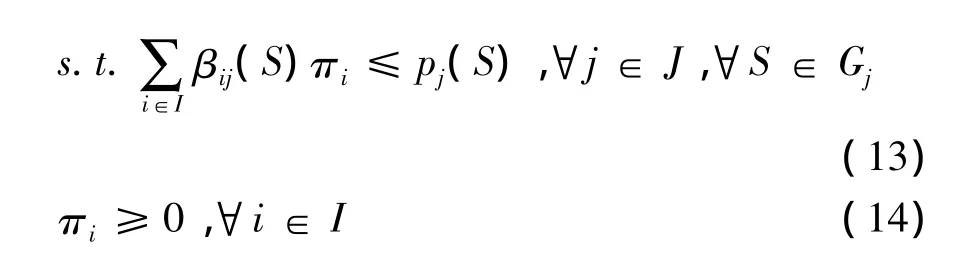
当上述LP的最优解为整数时，则其最优解即为WDP的最优解，从而最优的对偶变量即为相应的单条线路运输作业的服务价格。于是，可以把这些价格解释为单条线路运输作业的边际成本。那么，投标者提交的任何线路组合就可以定价了，即把该组合中所有单条线路运输作业的服务价格加起来即等于该组合的价值。然而，LP的解经常是分数，互补松弛条件不能得以满足。因此，单条线路运输作业的服务价格可能不存在。此时，DP的最优目标值只是代表了WDP最优目标值的一个严格下界。类似于资源分配设计（RAD）机制中价格的构造方法，笔者对已经获得暂时指派的组合和未获得暂时指派的组合分别设置约束条件，得到如下限制对偶问题（RDP）:

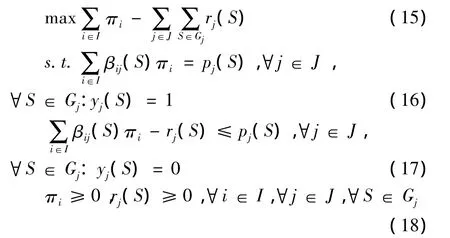
因为rj（S）可以取任意大的值，所以RDP总有可行解。rj（S）可以解释为价格歧视项，它可以避免暂时未获得指派的组合S的投标价小于该组合中各单条线路运输作业的价格之和。在多轮下降组合拍卖的背景下使用价格歧视，正的rj（S）将避免虚假套利。因为当投标者j的组合S未获得暂时指派时〔即yj（S）=0〕，如果单条线路运输作业的价格之和大于投标者j的投标价，则投标者j在下一轮能够对组合S中的每一条单条线路运输作业分别投标，并得到该组合的一个更高的投标价。这必将引起误导，因为在下一轮，对该组合的要求报价至多为pj（S）-ε，从而导致不必要的投标。

通过求解RDP，得到服务单个运输作业的近似价格（πi）和未获得暂时指派组合的歧视项〔rj（S）〕。当歧视项非零时，未获得暂时指派的组合中所包含的单条线路运输作业的服务价格之和并不能真正代表其边际成本，其值减去歧视项可能更能代表该组合的服务成本。

在拍卖的每一轮开始之前，拍卖者将宣布一组单条线路运输作业的服务价格πi（i∈I）和一组对应具体组合的歧视项。每一个投标者会求解其本身的决策子问题，在本轮要求报价的约束下，对使其效用最大化的所有组合进行投标。在拍卖第一轮开始时，投标者可以根据拍卖者宣布的单个作业的最大服务价格对组合进行定价和投标。

3.2 内生投标机制

假设在拍卖的任意一轮中，关于当前指派的RDP所构造的单线路运输作业服务价格πi（i∈I）存在。于是，在拍卖的第t轮，给定一组运输作业的服务价格πi（i∈I）和一组对应具体组合的歧视项rj（S），投标者j的最佳反应集为:

如果SDP有多组最优解，则投标者j可以任选其中一组最优解对应的线路组合进行投标。下面给出内生投标组合的定义:

设Hj={投标者j在拍卖开始之前所提交的组合S⊆I}。若在第t（t＞1）轮，投标者j提交的组合

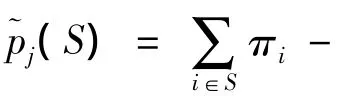
由上述定义可见，内生投标保持了投标者的近视最佳反应的性质。内生投标组合的产生使得投标者在拍卖过程中可以不断更新要提交的最优组合，从而避免了在拍卖开始之前列举和定价所有相关组合的麻烦。

3.3 内生投标的要求报价

由于在内生投标机制下也有外生投标组合（即在拍卖开始之前就确定好了的组合），因而此时的要求报价分以下几种情况:

1）对于在第t-1轮中未获得暂时指派的内生投标组合S来说，在第t轮对它的投标要求报价至多为:

式中:unhappy代表在第t-1轮中未中标的投标者。

2）如果某个在第t-1轮无人投标的组合S在第t轮是某个投标者的内生投标组合，则对它的要求报价至多为:

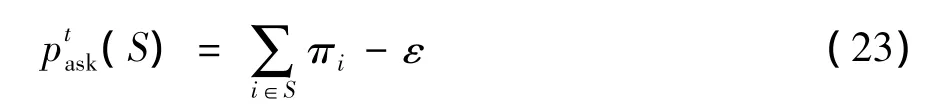
3）如果某个在第t-1轮获得暂时指派的组合在第t轮是某个投标者的内生投标，则该组合对于该投标者在第t轮的投标要求报价至多为第t-1轮的获胜投标价，即:

4）对于在第t-1轮中未获得暂时指派的外生投标组合S来说，在第t轮对它的投标要求报价至多为:

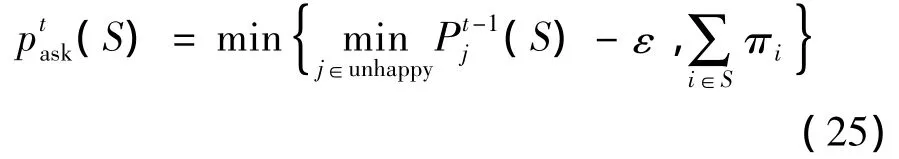
这样，内生投标保持了迭代拍卖中组合价格下降的性质。

3.4 内生投标机制下的拍卖步骤

在内生投标机制下，按以下步骤进行拍卖:

1）在拍卖第1轮开始时，投标者根据拍卖者宣布的单独服务每个作业的最大价格而对组合进行定价和投标。

2）拍卖者计算WDP，明确当前的暂时获胜者。若满足拍卖结束规则（见1.4），则拍卖结束，该轮的暂时获胜者就是最终获胜者。

3）拍卖者求解RDP，得到服务单个运输作业的近似价格（πi）和未获得暂时指派组合的歧视项〔rj（S）〕。

4）拍卖者宣布一组单条线路运输作业的服务价格πi和一组对应具体组合的歧视项。每一个投标者求解其本身的SDP，在本轮要求报价的约束条件下，对使其效用最大化的所有组合进行投标。然后，转第2）步。

由于笔者所提出的内生投标机制既保持了迭代组合价格下降的性质，又保持了投标者的近视最佳反应的性质，而迭代拍卖机制的所有其它规则保持不变，因此根据关于拍卖机制有效性的性质可知，本拍卖机制在拍卖结束时将实现系统的最优指派。

4 算例分析

针对一个关于运输作业指派的采购拍卖的例子，用以直观地解释基于外生投标和基于内生投标的迭代下降组合拍卖在运作上的差异。

假设一个4PL公司要把a，b，c，d等4条不同线路的运输作业通过采购拍卖的方式指派给8个潜在的3PL企业（代理）。假定，每个代理指派到的线路总数最多不超过3条，且最终获得指派的代理数最多不超过3个，各代理可以对运输作业进行组合投标，但各组合之间不相交，即不包含相同线路的运输作业。假设每1个代理的最大运力都是30。表1给出了各代理对其投标组合的成本信息。

表1 私人成本信息Table 1 Private costs information

表2和表3分别给出了外生投标机制下和内生投标机制下迭代下降组合拍卖的结果。其中，外生投标中各轮的组合价格在表4中给出。两种情况下，投标减量都取ε=1，上标“*”表示各轮的暂时指派结果，上标“D”表示投标价格含有一个ε折扣（本拍卖允许投标者在最大化其效用的ε邻域内对组合进行投标）。每一轮“暂时获胜者”的选择都是通过求解WDP问题而决定的，即考虑4PL公司的采购成本最小化，并考虑先前提到的假设条件约束。

表2 外生投标结果Table 2 Exogenous bidding results

表3 内生投标结果Table 3 Endogenous bidding results

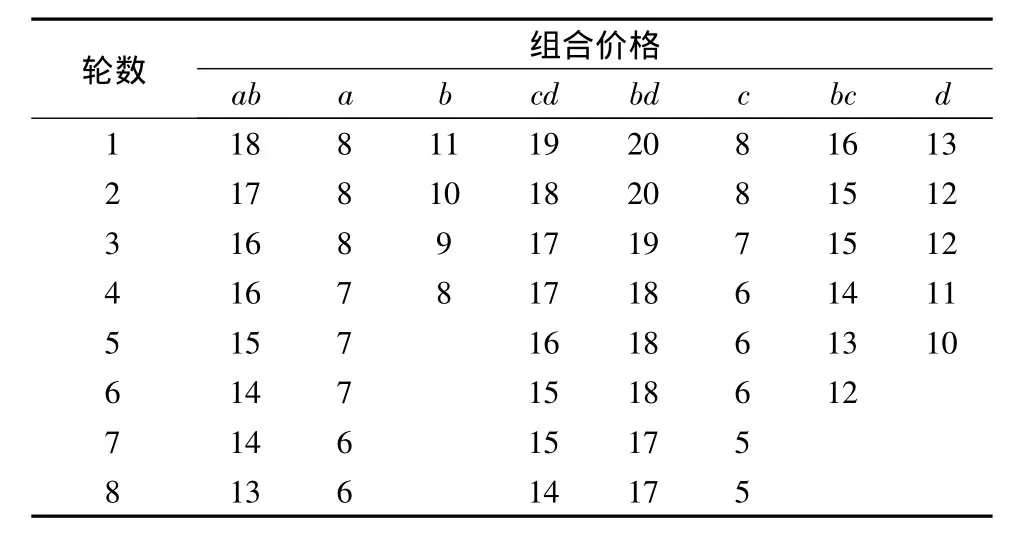
表4 外生投标中各轮的组合价格Table 4 Package prices for several rounds in exogenous bidding

在外生投标中，由于连续两轮出现了相同的投标，故拍卖结束。最后，由代理2以成本6服务线路a，代理5以成本17服务线路b和d，代理6以成本6服务线路c，4PL公司总的采购成本为29。该指派结果没有实现系统的最优指派。如前所述，这主要是由于外生投标限制了可选组合的空间所致。

在内生投标中，由于存在单条线路运输作业的服务价格，一些成本更低的组合被找出，使得那些在外生投标中未获得指派的投标者转而去竞争内生投标。价格歧视仅仅对于那些未获得暂时指派的组合来说才会发生，它导致受歧视组合的一个非线性价格。价格歧视的出现是由于该组合与当前获得暂时指派的组合之间在价格上的冲突造成的，因为要在DP问题中构建线性价格来满足这些组合的相应约束条件变得不可能。在本例中，价格歧视的出现主要是由于受到每个代理指派到的线路数最多不超过3条这个约束条件限制而引起的。比如，在第2轮中，本来使得4PL公司的采购成本最小化的暂时获胜组合是代理4投标的组合ab和组合cd，但由于受到中标线路数的限制，只能选择次优指派结果，即代理1投标的线路c，代理2投标的线路d和代理4投标的组合ab，于是组合cd受到歧视，同时组合bc也受到歧视。类似的情况出现在第5轮和第6轮中。在内生投标中，由于第7轮的所有投标者都是获胜者，故拍卖结束。最后，由代理3以成本15服务线路a和d，代理8以成本12服务线路b和c，4PL公司总的采购成本为27。该指派结果实现了满足相关约束条件下系统成本最小化的目标。由此看出，内生投标机制与外生投标机制相比，它能产生一个更有效的指派结果。

5 结语

考虑了4PL企业向3PL公司进行运输作业指派的迭代下降组合拍卖机制，其中投标者的内生投标组合决策被允许。内生投标机制的基础是利用近似单条线路运输作业的服务价格来找出拍卖之前未曾考虑的新的有利可图的组合。这些近似价格是通过一个限制对偶规划来构造的，它可以保持迭代拍卖的下降性质，同时避免无效的投标。数值试验显示，基于内生投标的迭代拍卖机制与基于外生投标的迭代拍卖机制相比具有更高的指派效率。在各3PL公司的成本函数为私有信息的情况下，4PL企业通过本拍卖机制可以淘汰成本结构差的3PL公司，从而优选出最有效率的3PL公司组合。因此，该模型为运输作业在3PL公司之间实现有效指派提供了决策支持。

（References）:

［1］ Caplice C G.An Optimization Based Bidding Process:A New Framework for Shipper-Carrier Relationships［M］.Cambridge，MA:MIT Department of Civil and Environmental Engineering，1996.

［2］ Ledyard J O，Olson M，Porter D，et al.The first use of a combined value auction for transportation services［J］.Interfaces，2002，32（5）:4-12.

［3］ Song J，Regan A C.Combinatorial auctions for transportation service procurement:the carrier perspective［J］.Transportation Research Board，2002，1833:40-46.

［4］ Sheffi Y.Combinatorial auctions in the procurement of transportation services［J］.Interfaces，2004，34（4）:245-252.

［5］ Lim A，Rodrigues B，Zhou X.Transportation procurement with seasonally varying shipper demand and volume guarantees［J］.Operations Research，2008，56（3）:758-771.

［6］ 杨华龙，东方，郑斌，等.集装箱航运服务多属性组合拍卖模型与算法［J］.交通运输工程学报，2009，9（5）:111-115.

Yang Hualong，Dong Fang，Zhen Bin，et al.Multi-attribute combinatorial auction model and algorithm for container shipping service［J］.Journal of Traffic and Transportation Engineering，2009，9（5）:111-115.

［7］ Rothkopf M，Pekec A，Harstad R.Computationally manageable combinatorial auctions［J］.Management Science，1998，44（8）:1131-1147.

［8］ Parkes D C，Ungar L H.Iterative Combinatoria1 Auctions:Theory and Practice［C］//Proceedings of 17th National Conference on Artificial Intelligence.Menlo Park，CA:AAAI Press，2000:74-81.

［9］ Kwon R H，Anandalingam G，Ungar L H.Iterative combinatorial auctions with bidder-determined combinations［J］.Management Science，2005，51（3）:407-418.

［10］ Guo Z，Koehler G J，Whinston A B.A market-based optimization algorithm for distributed systems［J］.Management Science，2007，53（8）:1345-1358.

Iterative Descending Combinatorial Auction Mechanism for Transportation Business Assignment Scheme

Li Liying
（School of Science，Chongqing Jiaotong University，Chongqing 400074，China）

An iterative descending combinatorial auction mechanism is proposed on the base of endogenous bidding，whose objective is to efficiently solve the truckload transportation business assignment problem of the 4PL company.By taking the dual of Winner Determination Problem（WDP），a restricted dual planning is structured;whose optimal solution provides a set of approximate single-lane prices.Bidders（3PL companies）can use this price information to determine new profitable packages before the next round under a myopic best response bidding strategy.Numerical experiment shows that the efficiency of assignments produced by using single-lane prices with endogenous bidding is greater than that of assignments produced in the exogenous bidding mechanism when bidding is restricted to a fixed set of packages determined before the start of the auction.

transportation business assignment;iterative combinatorial auction;myopic best response bidding strategy;endogenous bidding

F724.59

A

1674-0696（2013）02-0267-07

10.3969/j.issn.1674-0696.2013.02.21

2012-05-18;

2012-10-12

国家自然科学基金项目（70872123）

李莉英（1975—），女，四川自贡人，讲师，博士，主要从事物流与供应链管理等方面的研究。E-mail:lly-594@sohu.com。