气囊抛光工具与工件接触区压力及应力的分布规律研究

郑高安，方贵盛，金明生

(1.浙江水利水电学院机械电子工程系，浙江 杭州 310018;2.浙江工业大学机械工程学院，浙江 杭州 310032)

0 引言

基于柔性抛光理念的气囊抛光技术在超精密加工中占有重要的地位.气囊抛光工具具有柔性大、顺从接触性强、气压在线可控性高等特点，对其与工件表面接触区压力与应力分布规律探究是寻找保证被加工表面质量方法的重要前提.

在弹性体接触处应力状态研究中给出了令人满意分析的是Hertz接触理论［1］.随着工业方面上工程发展的促进，一些学者将Hertz接触理论与热弹性等式［2］相结合，并借助红外技术实现了两固体接触时接触区应力分布的可视化，使接触区应力分布研究更加直观［3－4］.

但，现有关于两物体接触区压力及应力分布研究主要集中在两种接触材料均为硬度较高的金属物体的接触问题上.关于气囊等弹性体与金属工件表面接触处的应力分布规律研究，虽有学者给出了相应的测量方法［5］，但在接触处压力分布及气囊变形情况上分析较少.

本文针对气囊抛光工具等弹性体与金属工件接触区的压力和应力分布以及气囊变形等问题开展研究，分析了不同材料特性与壁厚的气囊与金属工件接触时接触区的压力和应力分布特征以及气囊接触变形情况;同时借助于唯象理论，亦即不涉及分子结构的概念而基于数学推理的方法，获得气囊材料(橡胶)的本构模型，并结合有限元软件ANSYS对接触区应力进行仿真分析.

1 气囊本构模型

气囊本构模型是反映气囊应力与应变关系的模型.柔性抛光工具中的气囊，其拉压变形小于30%，纯剪切变形不超过75%，属于橡胶小变形范围.因此，本文选择橡胶类常用的Mooney-Rivlin模型［6］作为气囊物理特性研究的本构模型.该模型能很好地描述变形小于150%的橡胶材料力学性能，基本能满足橡胶材料实际应用的性能计算需要.Mooney—Rivlin模型为:

式(1)中:W—橡胶材料的应变能密度;

I1、I2—变形张量不变量;

C1和C2分别为橡胶材料的两个弹性常数，其常用的测定方法为单轴向拉伸、平面拉伸、双轴向拉伸等.本文以单轴向拉伸方法进行橡胶力学性能的测试，获得C1，C2.气囊的本构模型是进行气囊接触应力仿真的理论基础.

2 气囊与金属工件接触区的压力与变形分析

柔性抛光工具中的气囊根据其结构、厚度和材料的不同，其与金属工件接触时的接触区压力和应力分布以及接触部位气囊的变形形状也各有不同.下面选用柔性抛光工具中最典型的半球形气囊作为研究对象，对不同壁厚和材料属性的半球形橡胶气囊与金属工件接触时接触区压力分布和变形特征进行分析.

2.1 大厚度，高硬度的气囊

对于厚度较大，硬度较高的半球形橡胶气囊，可以将它看成一个橡胶球头来分析.因此，这类橡胶气囊与金属平面工件的接触，可由式(2)弹性接触Hertz理论给出的压力分布以及接触区外变形表面的形状表示于图1中.在r＜a的圆形域内，压力分布符合Hertz压力;在r=a的尖角处，变形后的轮廓与平表面相遇，该处有无穷大的拉力.实际上，应力不是无穷大，角也不是完全尖锐的，而有某个圆角，直到表面力与绘于图1中的力—间隙规律相一致.

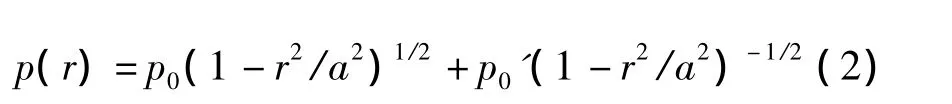
式(2)中:a—接触区域的圆形半径;

r—到圆形接触区域中心的距离;

p0=2aE*/πR，E*为结合模量.

图1 大厚度，高硬度气囊与金属平面工件接触的接触区压力和变形

2.2 普通厚度(壁厚在3 mm左右)，低硬度气囊

对于普通厚度，硬度较低的半球形橡胶气囊，其接触表面的压力以及变形与大厚度高硬度的气囊相比有很大的不同，见图2.气囊受力后容易变形，外加气囊的球形形状使它成为不可展曲面.当气囊受压与金属平面工件接触时，最初球壳的接触部分变平，因而产生薄膜压应力.当达到临界压力时，气囊因凹陷变形而在接触区屈曲，其接触力集中在气囊屈曲后与金属平面接触的接触面上，成环形分布.同时，由于气囊球面弯曲刚度和气囊圆柱壳的支撑作用，在接触面的端部引起压力的峰值.

图2 气囊屈曲变形后与金属平面工件接触的接触区压力分布

2.3 超薄，超弹性气囊

超薄超弹性气囊在充气或受外力作用下，极易变形，如同一个气球.根据薄膜模型，接触压力在接触区域内分布是均匀的，并且等于内部气压产生的膨胀压力.

3 气囊与金属工件接触区的应力仿真分析

对于柔性抛光工具中的气囊厚度，无统一的划分标准，其主要依据加工工艺的要求而选择.为此，本文选择壁厚为0.5 mm，3 mm与15 mm的三种气囊以分别代表超薄、普通厚度与大厚度的气囊，并以气囊工作时的正常下压量对其与金属工件接触区进行应力仿真分析.图3、图4、图5分别为0.5 mm，3 mm，15 mm三种厚度气囊的接触区应力仿真.从图3、图4、图5中的(b)分图可以得知，0.5 mm 厚度气囊的接触区应力呈微凹形状，两端应力突起部份是由于气囊圆柱壳的支撑作用引起，接触区应力分布总体趋于均衡;3 mm厚度气囊接触区应力明显趋于“M”型，即气囊接触时发生明显屈曲，端部出现应力峰值;15 mm厚度气囊接触区应力呈“Λ”型分布，峰值出在现在中心部位.仿真结果与气囊在接触区之间的压力分布相似，薄型气囊相对于大厚度和普通厚度两种气囊，其接触区应力分布更趋于均匀化.

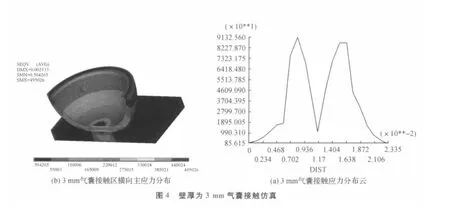
图5 壁厚为15 mm气囊接触仿真

4 结论

(1)柔性抛光工具中的半球形气囊随着壁厚与硬度的减少，其与金属平面工件接触时接触区之间的压力和应力分布由“Λ”型向“M”型再向“n”型转变，逐渐趋于均匀.

(2)半球形气囊与金属平面工件接触时接触区之间的压力和应力分布特征相似，但不同材料特性与厚度的气囊其接触变形有很大同.普通厚度的气囊在一定下压量下屈曲变形明显.为此，这类气囊在进行抛光加工时应注意其变形控制.

［1］约翰逊K L.接触力学［M］.徐秉业，译.北京:高等教育出版社，1992:103 －119.

［2］GASPER B C.Stress Analysis by Thermoelastic Techniques［C］.Proceedings of the International Society of Optical Engineer.Bellingham W A:SPIE，1987:233 pages.

［3］SAKAGAMI T，OGURA K，KUBO S，et al.Visualization of Contact Stress Distribution Using Infrared Stress Measurement System［C］//Richard N.Wurzbach.Proceedings of the International Society of Optical Engineer.Bellingham WA:SPIE，1997:250 －259.

［4］BRUSTENGA G，BORGARELLI N，MARSILI R.Measurement of Contact Pressure Distributions between Mechanical Components by Thermoelasticity［C］//The Japan Society of Mechanical Engineers.Asian Conference on Experimental Mechanics.Nagoya:ATEM＇03，JSME-MMD，2003:10 －12.

［5］计时鸣，郑高安，金明生，等.柔性抛光工具与工件接触区应力的测量方法与分布规律研究［J］.中国机械工程，2011，22(9):1107－1111.

［6］郑明军，王文静，陈政南，等.橡胶Mooney－Rivlin模型力学性能常数的确定［J］.橡胶工业，2003，50(8):462－465.