Bitranslations of com p letely sim p le sem igroups and some applications

YANG Yuhui，ZHANG Jiangang

（College of Mathematics and Sciences，Shanghai Normal University，Shanghai 200234，China）

Bitranslations of com p letely sim p le sem igroups and some applications

YANG Yuhui，ZHANG Jiangang

（College of Mathematics and Sciences，Shanghai Normal University，Shanghai 200234，China）

We discuss the bitranslations of completely simple semigroups by the representations given by Petrich M.As an application，we get the structure of an inflation of a completely simple semigroup.Furthermore，we consider the isomorphism between two inflations of completely simple semigroups.

completely simple semigroup；bitranslation；inflation

1 Introduction and notations

Lallement G.reduced the structure of completely regular semigroups to that of completely simple semigroups and certain functions among them and their translational hulls in［1］.Petrich M gave the representation of the wreath product of left，right translations and bitranslations of a completely simple semigroup in［2］and［3］.Zhang JG，etc.considered the properties of bitranslations of completely simple semigroups in［4］by the representation of the wreath product.In this paper，we discuss the bitranslations of completely simple semigroups by another representation of them given by Petrich M.Furthermore，we get the structures of inflations of completely simple semigroups and isomorphisms between two inflations of completely simple semigroups.

An element a of a semigroup S is said to be regular if there exists an x in S such that a＝axa.The semigroup S is said to be regular if all its elements are regular.A regular semigroup S is said to be completely regular if every element of S lies in a subgroup of S.A completely simple semigroup is completely regular and simple.By Rees′s theorem，every completely simple semigroup is isomorphic to a Reesmatrix semigroup.

Let S be a semigroup and x，y be arbitrary elements of S.A mapλon S，written on the left，is a left translation ifλ(xy）＝(λx）y；amapρon S，written on the right，is a right translation if(xy）ρ＝x(yρ）；the pair (λ，ρ）is a bitranslation if in addition x(λy）＝(xρ）y，λandρare also said to be linked.The setΛ(S）of all left translations of S is a semigroup under the composition(λλ′）x＝λ(λ′x）；the set P(S）of all right translations of S is a semigroup under the composition x(ρρ′）＝(xρ）ρ′；the subsemigroupΩ(S）ofΛ(S）× P(S）consisting of all bitranslations is the translational hull of S.Specially，λaandρaare linked obviously，whereλax＝ax and xρa＝xa，for some a∈S.

Throughout this paper，the symbol S denotes a Reesmatrix semigroup M(I，G，Λ；P），where G is a group with identity e and P＝(pλi）is the sandwichmatrix.The elements of S are denoted by(i，g，λ），where i∈I，g∈G andλ∈Λ.Let J⊂I and M⊂Λ.The symbol SJ×Mdenotes the subset｛(i，g，λ）∈S：i∈J，g∈G，λ∈ M｝of S.The setof idempotents of a semigroup S is denoted by E(S）.An idempotent(i，λ）of S is denoted by eiλ.Let J⊂I and M⊂Λ.Then the symbol EJ×Mdenotes the subset｛eiλ∈E(S）：i∈J，λ∈M｝of E (S）.

Notation 1.1［5］In this section，we set S＝M(I，G，Λ；P）with P normalized at1∈I∩Λ.Let

with multiplication(F，g，Φ）(F′，g′，Φ′）＝(FF′，gp1Φ，F′1g′，ΦΦ′），where J′(I）is the set of allmaps in I and J(Λ）is the set of allmaps inΛ.

Lemma 1.1［5］Let S＝M(I，G，Λ；P）with P normalized，and let e be the identity of G.Define amappingσby

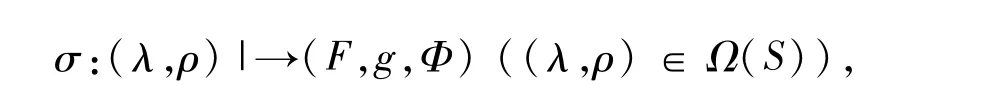
where F，g andΦare defined by the requirements

Further，we define amappingτby

whereλandρare defined by the formulae

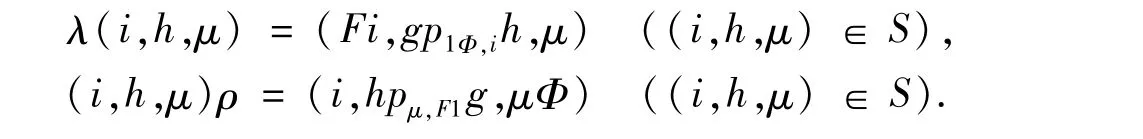
Thenσandτaremutually inverse isomorphisms betweenΩ(S）and T(S）.Moreover

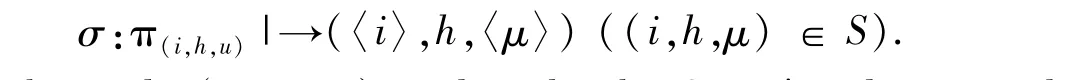
In this paper，we use the triple(F，g，Φ）to describe the Green′s relations and inner bitranslations of completely simple semigroups.Let a∈S and P be a Green′s relation，the symbol Padenotes the P-class of S containing a.

The reader is refered to［5-7］for definitions and symbols notmentioned here.

2 Bitranslations of completely simple semigroups

Let i，j∈I，λ，μ∈Λ，and set

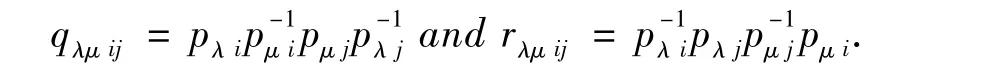
Then it is easy to verify the following results.

Lemma 2.1Let S be a completely simple semigroup.The following conditions are equivalent：

(1）qλμij＝e，

(2）rλμij＝e，

(3）E｛i，j｝×｛λ，μ｝is a subband of S.

Proposition 2.1Let(F，g，Φ）∈T(S）.Then for any i，j∈I，λ，μ∈Λ，we have

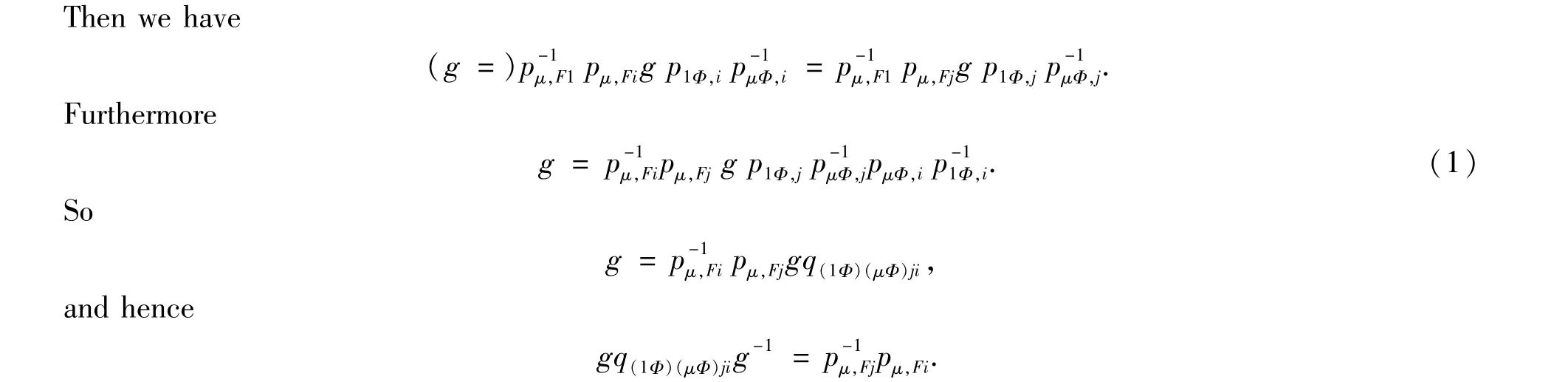
Similarly，(2）can be proved.

The converse part is easy to see.

LetιI，ιΛbe the identitymappings on I，Λ.Then we have the following corollary.

Corollary 2.2The identity of T(S）is(ιI，e，ιΛ）.

3 Some applications

A semigroup S is an inflation of a semigroup K if K is a subsemigroup of S and there is amappingφ*of S into K such that

Let Q be a partial semigroup and K＝M(I，G，Λ；P）be a Reesmatrix semigroup over a group G，such that Q∩K＝Ø.Letξ：p｜→i be amapping from Q into I on the left，η：pλbe amapping from Q intoΛon the right andφ：p｜→g be amapping from Q into G on the right side.

Let us define amultiplication on S＝Q∪K with

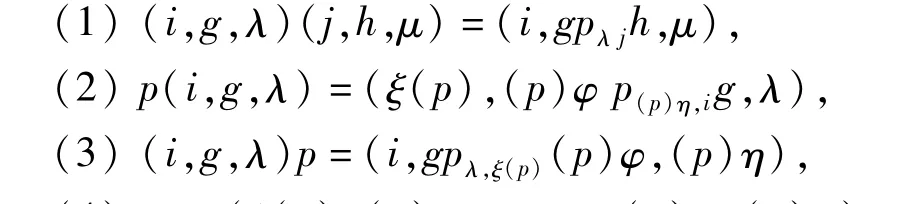
(4）pq＝(ξ(p），(p）φp(p）η，ξ(q）(q）φ，(q）η）， for all p，q∈Q；g，h∈G；i，j∈I andλ，μ∈Λ.Then S with themultiplication defined above will be denoted by M(I，G，Λ；P；Q；φ，ξ，η）.

Lemma 3.1M(I，G，Λ；P；Q；φ，ξ，η）is a semigroup.

ProofIt is clear that themultiplication iswell defined.

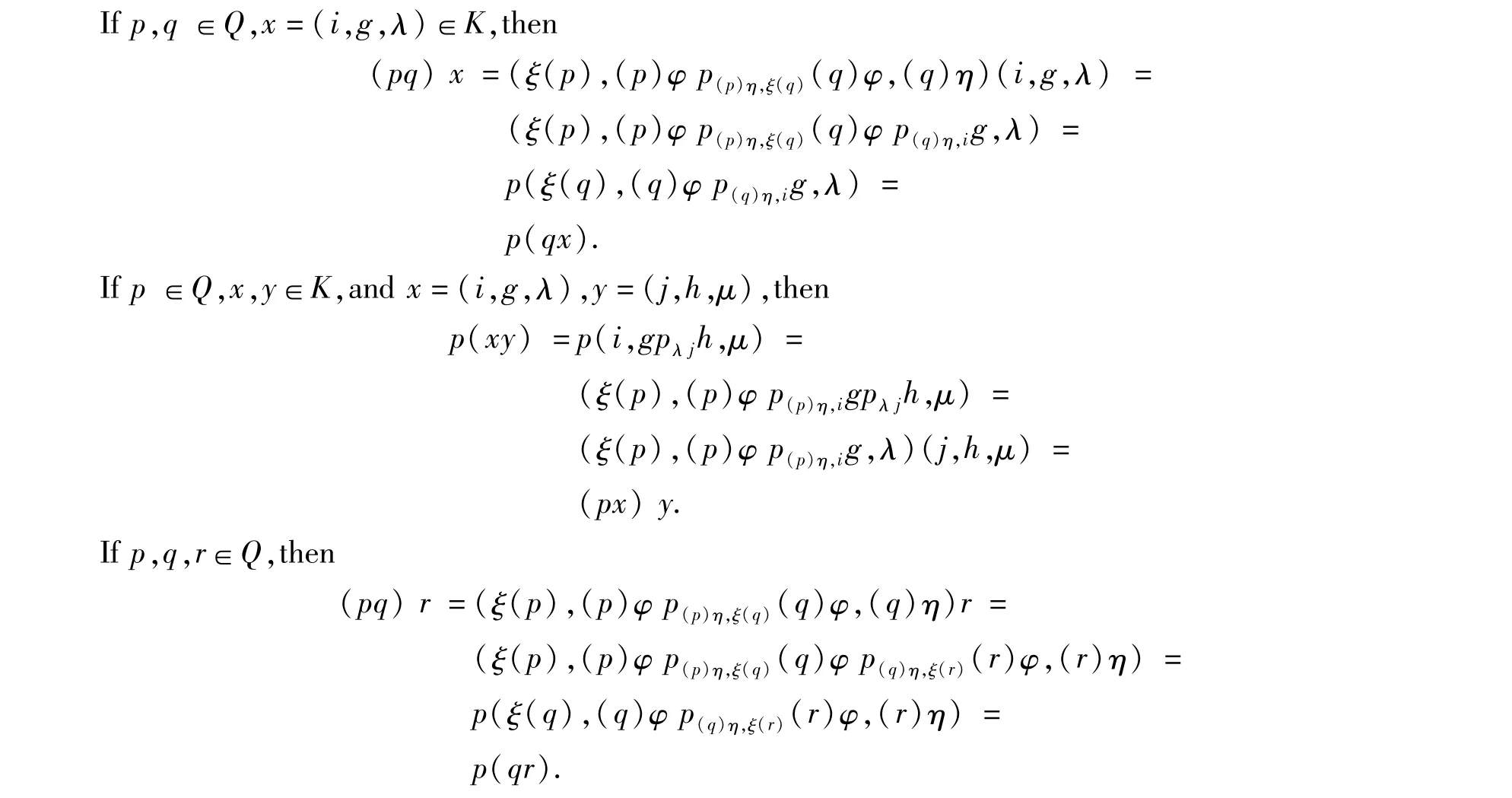
The other cases can be proved similarly.So M(I，G，Λ；P；Q；φ，ξ，η）is a semigroup.

Theorem 3.1S is an inflation of a completely simple semigroup K if and only if S is isomorphic to some M(I，G，Λ；P；Q；φ，ξ，η），where K＝M(I，G，Λ；P）.

ProofLet S be an inflation of a completely simple semigroup K.Then the Reesmatrix semigroup K is the kernel of S，and Q＝S＼K is a partial semigroup.For any p∈Q and(j，h，μ）∈K，ifφ*(p）＝(i，g，λ），we have

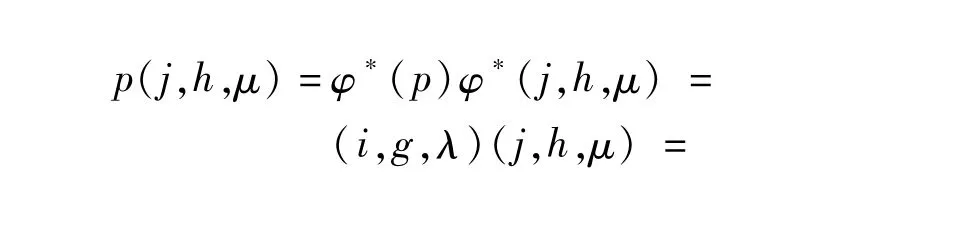
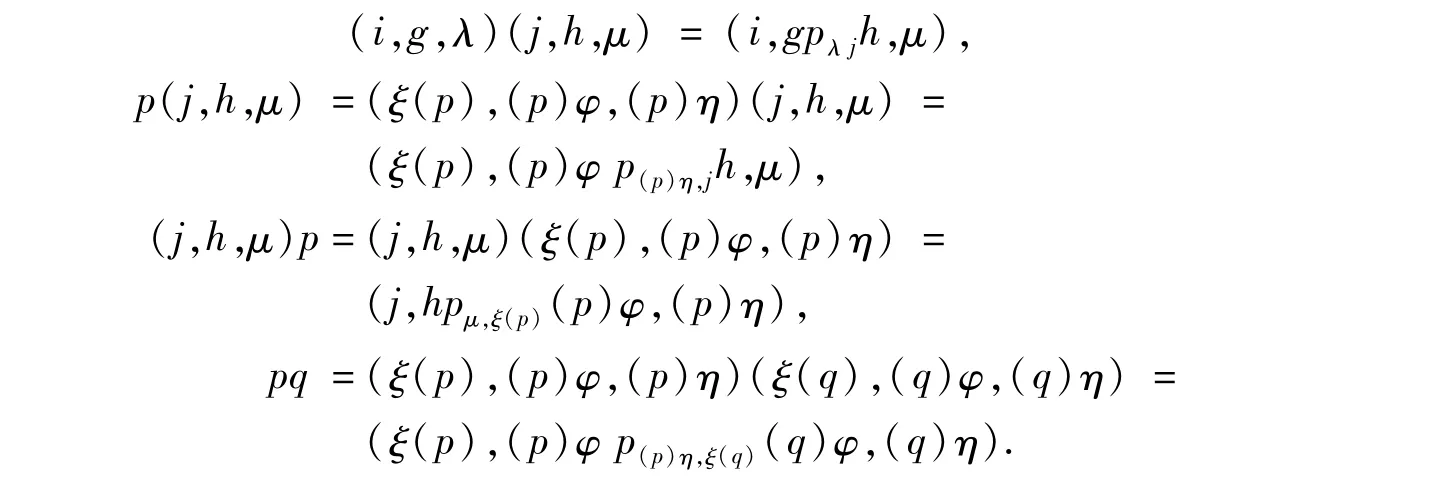
Hence we get S＝M(I，G，Λ；P；Q；φ，ξ，η）.

Conversely，if S＝M(I，G，Λ；P；Q；φ，ξ，η），by Lemma 3. 1，S is a semigroup and K＝M(I，G，Λ；P）is the kernel of S.Define amappingφ*：SK satisfying that

(1）for any(i，g，λ）∈K，φ*(i，g，λ）＝(i，g，λ），

(2）for any p∈Q，φ*p＝(ξ(p），(p）φ，(p）η）.

Sinceξ，φ，ηaremappings，soφ*iswell defined.

For any(i，g，λ），(j，h，μ）∈K，p，q∈Q，we have

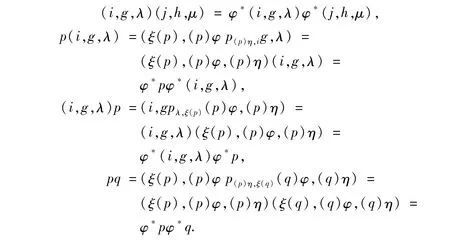
Hence，S is an inflation of the completely simple semigroup M(I，G，Λ；P）.

Theorem 3.2

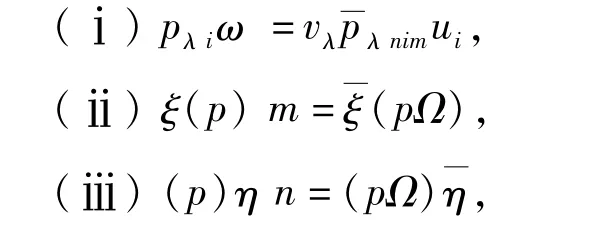
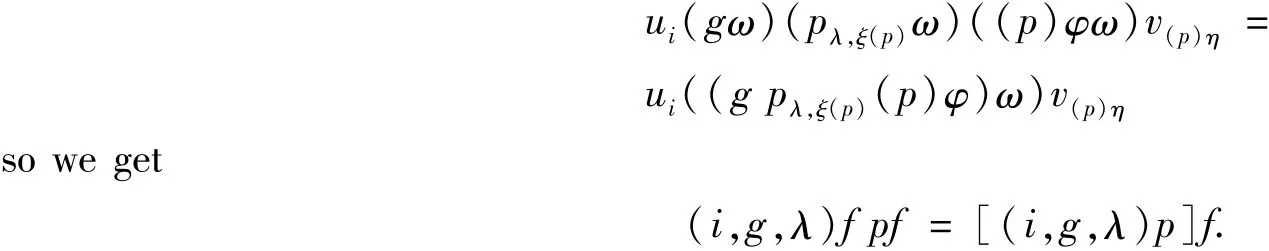
［1］ LALLEMENT G.Demi-groups reguliers［J］.Ann Mat Pura Appl， 1967，77：47-129.

［2］ PETRICH M.The translational hull of a completely 0-simple semigroup［J］.Glasgow Math， 1968，9：1-11.

［3］ PETRICH M.The structure of completely regular semigroups［J］.TAMS， 1974，189：221-236.

［4］ SONG G T，ZHANG JG，LIU G X.Bitranslations of Completely Simple Semigroups［J］.Southest Asion Bulletion ofMathematics， 2006，30：107-122.

［5］ PETRICH M，REILLY N.Completely Regular semigroups［M］.New york：John Weley＆Sonc INC，1999.

［6］ HOWIE JM.Fundamentals of Semigroup Theory［M］.Oxford：Oxford University Press Inc，1995.

［7］ STOJAN BOGANOVIC.Semigroupswith a System of Subsemigroups［M］.Novi Sad：University of Novi sad Institude of Mathematic，1985.

（责任编辑：冯珍珍）

完全单半群的平移包及其应用

杨禹慧，张建刚

(上海师范大学数理学院，上海200234）

利用Petrich M.关于完全单半群的平移包的表示进一步研究了完全单半群平移包的性质.作为应用，给出了完全单半群膨胀的结构和它们之间的同构.

完全单半群；平移包；膨胀

O 152.7

A

1000-5137（2013）02-0111-09

Received date：2013-01-12

Foundation item：National Natural Science Foundation of China( 11201305，11001046）；Innovation Projectof Shanghai Education Committee(12YZ081）

Biography：YANG Yuhui(1987-），female，graduate student，College of Mathematics and Sciences，Shanghai Normal University；ZHANG Jiangang(1977-），male，associate professor，College ofMathematics and Sciences，ShanghaiNormal University.