The viscoelastic effects on thermal convection of an Oldroyd-B fluid in open-top porous media*

NIU Jun (牛骏), SHI Zai-hong (石在虹)

Petroleum Exploration and Production Research Institute of SINOPEC, Beijing 100083, China,

E-mail: niujun.syky@sinopec.com

TAN Wen-chang (谭文长)

State Key Laboratory for Turbulence and Complex Systems and Department of Mechanics and Aerospace Engineering, College of Engineering, Peking University, Beijing 100871, China

The viscoelastic effects on thermal convection of an Oldroyd-B fluid in open-top porous media*

NIU Jun (牛骏), SHI Zai-hong (石在虹)

Petroleum Exploration and Production Research Institute of SINOPEC, Beijing 100083, China,

E-mail: niujun.syky@sinopec.com

TAN Wen-chang (谭文长)

State Key Laboratory for Turbulence and Complex Systems and Department of Mechanics and Aerospace Engineering, College of Engineering, Peking University, Beijing 100871, China

(Received July 18, 2013, Revised July 24, 2013)

The effects of two viscoelastic parameters on the thermal convection of a viscoelastic Oldroyd-B fluid in an open-top porous square box with constant heat flux are investigated. The results show that the increase of relaxation time is able to destabilize the fluid flow leading to a higher heat transfer rate, while the increase of retardation time tends to stabilize the flow and suppress the heat transfer. The flow bifurcation appears earlier with the increase of the relaxation time and the decrease of the retardation time, resulting in more complicated flow patterns in the porous medium.

viscoelastic effect, thermal convection, Oldroyd-B fluids, porous medium

Thermal convection of viscoelastic Oldroyd-B fluids in porous media is an issue of great importance, as applications are found in many fields such as bioengineering and oil reservoir engineering[1]. However, due to the lack of a simple model for the description of viscoelastic flow behavior, the studies of thermal convection of Oldroyd-B fluids in porous media are far less than fruitful as compared with those of Newtonian fluids[2,3].

Recently, the modified Darcy’s law[4]has drawn much attention in the research of thermal instability problem of Oldroyd-B fluid saturated porous media heated from below. With the modified Darcy’s law, Fu et al.[5]numerically analyzed the thermal convection of an Oldroyd-B fluid in an impermeable porous square box heated from below with a constant bottom temperature. It is found that the thermal convection of Oldroyd-B fluids in porous layers has earlier bifurcations with the increase of the Darcy-Rayleigh number than that of Newtonian fluids. Therefore, their heat transfer characteristics are quite different. However, to the best of our knowledge, no results have been published for thermal convection of an Oldroyd-B fluid in an open-top porous medium under a constant heat flux boundary condition. The objective of this work is to investigate the viscoelastic effects on the thermal convection of an Oldroyd-B fluid in an open-top porous medium with a constant heat flux.

Our model is a bounded two-dimensional square porous medium of thickness H. The top horizontal boundary of the medium is isothermal with a constant temperature0T, and is permeable along which the pressure is assumed as a constant. The impermeable bottom boundary is exposed to a constant heat flux q. The two vertical boundaries are adiabatic and impermeable. The porous medium has a permeability K and is saturated by an incompressible Oldroyd-B fluid with a constant dynamic viscosity μ, a coefficient of thermal expansion β and a density ρ. The fluid-saturated porous medium has a thermal conductivity k and thermal diffusivity κ. The modified Darcy’s law is employed in this work leading to the following governing equations[5]

Here, lengths are non-dimensionalized with H, time with2/Hκ, temperature with /qHk, and velocities with /Hκ. The Darcy-Rayleigh number =Ra KβρgH2q/μkκ is the dimensionless parameter de-0termining the vigor of convection within the porous medium.are dimensionless relaxation and retardation and relaxation times, respectively. The constant pressure boundary condition is converted into an equivalent velocity boundary condition

The bulk-averaged Nusselt number Nu is used to estimate the convection heat transport characteristics in the porous medium, which is given by =Nuwith the angle brackets indicating the long-time average. Equations (5) - (7) are numerically solved with the program we coded based on the finite difference method.

Our most interest to investigate the effects of the parameters λ and ε on the heat transport characteristics and flow patterns. We consider the following parameter pairs: (1) =0.3λ, =0.2ε, (2) =0.2λ, ε=0.1, (3) λ=0.3, ε=0.1 and calculate the flow and the heat transfer for each case. As Cases (2) and (3) have the same retardation time value, the results can be used to analyze the effect of the relaxation time. Similarly, the comparison of results of Cases (1) and (3) may reveal the effect of retardation time value.

Fig.1 Comparison of the heat transfer curves for the three cases of the Oldroyd-B fluid. Also shown is the curve for a Newtonian fluid

The bulk-averaged Nusselt number Nu as a function of the Darcy-Rayleigh number Ra up to 400 are shown in Fig.1 for the three cases of λ and ε as well as Newtonian fluid case. For Cases (1) and (2), interestingly, parts of the two heat transfer curves almost overlap with that for a Newtonian fluid. It can be inferred from this phenomenon that the steady convection after onset can suppress the oscillatory convection and dominate the convection process, as has also been observed in the previous work[5]. This trend persists for Ra up to about 45. As Ra further increases, the heat transfer curve for Case (2) separates first from the curve for a Newtonian fluid and is located above the Newtonian fluid curve. The heat transfer curve for Case (1) will also separate from that for a Newtonian fluid when Ra is larger than about 50. However, contrary to the curve for Case (2), it is located below the curve for a Newtonian fluid when Ra is in the range between 50 and 175. There is a sharp increase in the heat transfer rate for Case (1) at Ra=185, such that this curve jumps up and intersects the curve for a Newtonian fluid at Ra around 200. The heat transfer curve for Case (3), however, has no part overlapping with that for a Newtonian fluid and is located totally above the other three curves shown in Fig.1. These distinct properties of the heat transfer process for Cases (1), (2) and (3) are caused by a series of transitions of the flow pattern inside the porous medium, which in turn are affected by the viscoelasticity of the fluid, as will be discussed in detail later on.

Comparing the curves in Fig.1 for Cases (1) and (3), in which =0.3λ and ε is equal to 0.2, 0.1, it can be seen that a larger value of ε corresponds to a smaller Nu. Therefore, the increase of the retardation time tends to suppress the heat transfer. The curves forCases (2) and (3), in which =0.1ε and λ is equal to 0.2, 0.3, show that the increase of the relaxation time can enhance the heat transfer rate.

For the Oldroyd-B fluid, due to the viscoelasticity, both the oscillatory convection mode and the steady convection mode may co-exist after the onset of thermal convection. For Case (1), the steady convection mode dominates the heat transfer process for Ra up to 50. In this range, the flow exhibits a steady one-cell roll pattern and the heat transfer curve overlaps with that for a Newtonian fluid.

Fig.2 Successive snapshots of the stream function contours for Case (1) at =125Ra with a time interval 0.2, showing the flow is in a one-cell roll alternating with the two-cell roll pattern

Fig.3 The time history of Nu and the power spectrum for Case (1) at Ra=125

When Ra is greater than 50, the heat transfer curve for Case (1) deviates from that for a Newtonian fluid and becomes lower than the Newtonian fluid curve. The convection can no longer remain a steady one-cell roll state, but exhibits a flow pattern of a onecell roll alternating with a two-cell roll. Figures 2(a)-2(d) show the snapshots of the stream function contours for Case (1) at =125Ra, with a time interval equal to 0.2. The one-cell roll alternating with the two-cell roll flow pattern is clearly seen and the outer contours of the stream function do not cross the opentop boundary vertically, but bends towards the center of the flow circulation.

Figure 3(a) shows the time history of Nu for Case (1) at =125Ra, which reveals that the thermal convection is in a quasi-periodic state. Plotted in Fig.3(b) is the corresponding power spectrum of Nu, in which three prevailing frequencies can be identified: f1=1.33, f2=3.1 and f3=f1+f2=4.43. On the other hand, the flow pattern for a Newtonian fluid at Ra=125 is a steady two-cell roll (it is a one-cell roll for Ra=50), resulting in a quick increase in the heat transfer rate. Therefore, though the oscillatory convection due to the viscoelasticity of the fluid affects significantly the heat transfer process, the heat transfer rate for Case (1) can be lower than that for a Newtonian fluid at the same value of Ra.

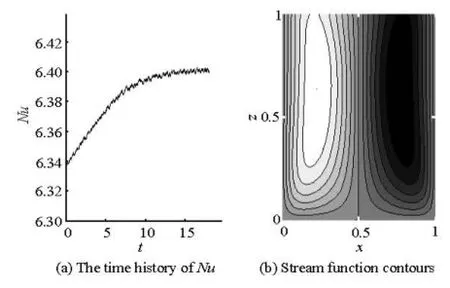
Fig.4 The time history of Nu and contours of the stream function for Case (1) at =185Ra

The heat transfer curve for Case (1) jumps sharply up almost to merge with that for a Newtonian fluid at Ra=185, which indicates the occurrence of another flow pattern transition. Shown in Fig.4(a) is the time history of Nu for Case (1) at =185Ra. In essence, this curve approaches a constant value in a long enough time and its characteristics are different from these shown in Fig. 3(a), though tiny oscillations can be found inherent in it. Figure 4(b) shows a snapshot of the contours of the stream function for Case (1) at Ra=185, a two-cell roll flow pattern is clearly seen. Unlike that shown in Fig.2, this flow pattern persists at any time instant and represents the typical flow pattern. Furthermore, it is interesting to find that the contours of the stream function now change to cross the top boundary vertically, similar to the case for a Newtonian fluid in a steady two-cell roll state[6]. Therefore, it is concluded that the steady convection re-dominates the thermal convection process after the transition, but the effect of viscoelasticity is not com-pletely suppressed, which is manifested by the tiny oscillations in the Nu vs. t curve.

The two-cell roll flow pattern for Case (1) holds for Ra up to about 275, where the thermal convection experiences the third bifurcation and the flow pattern changes to an unsteady two-cell roll. This unsteady two-cell roll pattern further enhances the heat transfer rate, resulting in the enlargement of the distance between the heat transfer curves for Case (1) and that of the Newtonian case as Ra increases.

The thermal convection for Case (2) is also dominated by the steady convection after onset for Ra up to approximately 45. Therefore, the flow exhibits a steady one-cell roll pattern and the corresponding heat transfer curve in this range follows that for a Newtonian fluid. When Ra is further increased, however, the flow pattern for Case (2) will transit into unsteady one-cell roll alternating with a two-cell roll, and the heat transfer curve will deviate from that for a Newtonian fluid and become higher than the Newtonian fluid curve. This situation lasts for Ra up to 400.

Fig.5 Snapshots of the stream function contours for Case (3) at Ra=50, 100 and 250, showing the flow patterns after each bifurcation

The thermal convection for Case (3) exhibits very different phenomena from those for Cases (1) and (2). A thermal convection bifurcation occurs for Ra between 40 and 45, resulting in transition of the flow pattern from the one-cell roll to an unsteady twocell roll. Another bifurcation occurs for Ra between 65 and 75 and the flow pattern transits from the unsteady two-cell roll to an unsteady three-cell roll after the bifurcation. The third bifurcation appears for Ra between 200 and 225, and the flow pattern varies from the unsteady three-cell roll to an unsteady three-cell roll alternating with four-cell roll. Figures 5(a)-5(c) show the snapshots of the stream function contours for Case (3) at =Ra50, 100 and 250. The flow patterns seem to be under a close-top boundary, which may be induced by the high elastic effect.

From the above analysis, it can be concluded that the increase of the relaxation time and the decrease of the retardation time can facilitate earlier thermal convection bifurcation and complicates the flow pattern.

In summary, the effects of two viscoelastic parameters on the thermal convection of an Oldroyd-B fluid saturated in an open-top porous square box with constant heat flux are studied. The results reveal some unique characteristics of the thermal convection process. First, both the steady convection and the oscillatory convection are shown to be possible in the opentop porous medium. For fixed λ and ε, the oscillatory convection starts earlier than the steady convection. Second, the viscoelastic effect may either enhance or diminish the heat transfer rate comparing to the case for a Newtonian fluid at the same Rayleigh number, depending on the values of λ and ε. Third, a larger λ tends to destabilize the thermal convection leading to a higher heat transfer rate and earlier flow bifurcation, while a larger ε has the effect to stabilize the flow and simplify the flow pattern.

Our results may find applications in the oil engineering. As the heavy oil exhibits viscoelastic rheological behavior, our study suggests that using some chemical to increase its relaxation time parameter and decrease the retardation time parameter may lead to more efficient thermal recovery. Moreover, our work may also be applied to the analysis of fluid behavior underground with terrestrial heat, which may help the research of carbondioxide storage underground.

[1] NIELD D. A., BEJAN A. Convection in porous media[M]. 4th Edition, New York, USA: Springer-Verlag, 2013.

[2] SHAN Lian-tao, TONG Deng-ke and XUE Li-li. Unsteady flow of non-Newtonian visco-elastic fluid in dual-porosity media with the fractional derivative[J]. Journal of Hydrodynamics, 2009, 21(5): 705-713.

[3] ZHANG Li-juan, YUE Xiang-an. Mechanism for viscoelastic polymer solution percolating through porous media[J]. Journal of Hydrodynamics, Ser. B, 2007, 19(2): 241-248.

[4] BERTOLA B., CAFARO E. Thermal instability of viscoelastic fluids in horizontal porous layers as initial value problems[J]. International Journal of Heat and Mass Transfer, 2006, 49(21): 4003-4012.

[5] FU Ce-ji, ZHANG Zhi-yong and TAN Wen-chang. Numerical simulation of thermal convection of an Oldroyd-B fluid in a porous square box heated from below[J]. Physics of Fluids, 2007, 19(10): 104107.

[6] CHERKAUI A. S. M., WILCOCK W. S. D. Characteristics of high Rayleigh number two-dimensional convection in an open-top porous layer heated from below[J]. Journal of Fluid Mechanics, 1999, 394: 241-260.

10.1016/S1001-6058(11)60406-0

* Project supported by the National Key Basic Research Development Program of China (973 Program, Grant Nos. 2006CB705803, 2013CB531200).

Biography: NIU Jun (1985-), Male, Ph. D.

SHI Zai-hong, E-mail: shizaihong.syky@sinopec.com