Seasonal variability of the bifurcation of the North Equatorial Current*

JU Qiang-chang (琚强昌), JIANG Song (江松)

Institute of Applied Physics and Computational Mathematics, Beijing 100088, China,

E-mail: ju_qiangchang@iapcm.ac.cn

TIAN Ji-wei (田纪伟)

Physical Oceanography Laboratory, Ocean University of China, Qingdao 266100, China

KONG Ling-hai (孔令海), NI Guo-xi (倪国喜)

Institute of Applied Physics and Computational Mathematics, Beijing 100088, China

Seasonal variability of the bifurcation of the North Equatorial Current*

JU Qiang-chang (琚强昌), JIANG Song (江松)

Institute of Applied Physics and Computational Mathematics, Beijing 100088, China,

E-mail: ju_qiangchang@iapcm.ac.cn

TIAN Ji-wei (田纪伟)

Physical Oceanography Laboratory, Ocean University of China, Qingdao 266100, China

KONG Ling-hai (孔令海), NI Guo-xi (倪国喜)

Institute of Applied Physics and Computational Mathematics, Beijing 100088, China

(Received August 10, 2012, Revised November 10, 2012)

Seasonal variability of the bifurcation of the North Equatorial Current (NEC) is studied by constructing the analytic solution for the time-dependent horizontal linear shallow water quasi-geostrophic equations. Using the Florida State University wind data from 1961 through 1992, we find that the bifurcation latitude of the NEC changes with seasons. Furthermore, it is shown that the NEC bifurcation is at its southernmost latitude (12.7oN) in June and the northernmost latitude (14.4oN) in November.

North Equatorial Current (NEC), seasonal variability, quasi-geostrophic equations, analytic solution

Introduction

In the western Pacific, the North Equatorial Current (NEC) bifurcates into the northward flowing Kuroshio current and the southward flowing Mindanao current as it reaches the Philippine coast. The bifurcation latitude is a key index which directly determines the partition of mass, heat and salt between subtropical and tropical gyres, and the dynamical structure of the low-latitude western boundary currents. It is believed that the variation of the NEC bifurcation is crucial to the understanding of the climate dynamics[1-4].

The earliest description of the NEC bifurcation is attributed to Schott (1939). Until the 90s of the last century, the study of the NEC bifurcation was mainly based on data of one or several cruises. Using hydrographic data from various cruises between 1934 and 1968, Nitani (1972) showed that the bifurcation of the NEC at the sea surface occurs at 11oN to 14.5oN . On the basis of the water mass distribution along the western boundary, Tool et al. (1988) estimated that the NEC bifurcation is at the latitude around 12oN, while with two hydrographic surveys in September 1987 and April 1988, respectively, the NEC was observed to bifurcate near 13oN. But many studies began to focus on its seasonal and interannual variations due to the increasing amount of cruise data after 1990. Using the linear, time-dependent Sverdrup theory and the high-resolution nonlinear reduced-gravity model, Qiu-Lukas (1996) firstly studied the seasonal and interannual variations of bifurcation of the NEC. They showed that the bifurcation occurred at its southermost latitude in February and the northernmost latitude in October and took place at its highest latitude a year after El Niño and at its lowest latitude during the La Niña year. With historical hydrographic data, Qu and Lukas[5]constructed the climatology of temperature and salinity and found that the NEC bifurcation near the surface is at its southernmost latitude(13.4oN) in June and its northernmost latitude (14.8oN) in November, the NEC bifurcation is at its southernmost latitude (14.8oN) on the vertical average in July and its northernmost latitude (17.2oN) in December. Usingthe JAMSTEC Earth Simulator, Kim et al.[6]showed that the NEC bifurcation at the surface happened at its southernmost position (13.2oN) in May and its northernmost (15.1oN) in September. Using the WOCE float data in 1987-1998, Li et al.[7]estimated that the NEC bifurcate latitude is about 11oN-14.7oN and showed that it has an obvious interannual variation. Analyzing the 12 year altimetry data from October 1992, Wang and Hu[8]concluded that the NEC bifurcation is at its southernmost latitude (12.9oN) in June and its northernmost latitude (14.1oN) in December. Both Kim et al. and Wang and Hu found that the NEC bifurcation point was closely correlated to the ENSO. For more studies on the bifurcation of NEC, the interested readers can Refs.[9-13].

There exist differences in the seasonal and interannual variations and the position of the NEC bifurcation among the previous available results. These differences (even small in some cases) will lead to a very serious influence on the mass and heat transportation of the Mindanao and Kuroshio Currents. Therefore it is important to study the seasonal and interannual variations of the NEC bifurcation more extensively.

This paper studies the seasonal variation of the NEC bifurcation by using the linear, time-dependent shallow water quasi-geostrophic model and the Florida State University wind data from 1961 through 1992. As is known, there is very few theoritical studies of the seasonal variation of the NEC bifurcation. Recently, Wang et al.[14]obtained a series solution by the expansion method, which is very complicated. However we shall construct the analytic solution for the time-dependent shallow water quasi-geostrophic model based on the classical variable separation method and the solution of the Sturm-Liouville problem. With the help of thisanalytic solution and the Florida State University wind data from 1961 through 1992, the seasonal variability of the bifurcation of the North Equatorial Current will be investigated. It must be remarked that although the focus of this paper is on the seasonal wind, the arguments can be easily extended to include interannual wind changes.

1. The shallow water quasi-geostrophic model

We consider the linear viscous shallow water quasi-geostrophic model[15]

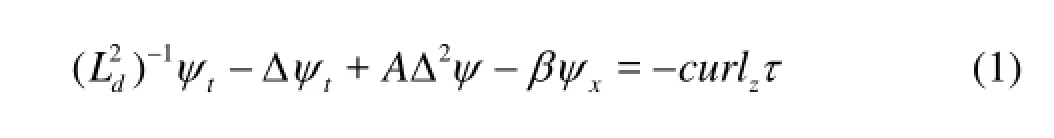
where ψ is the stream function and zcurlτ is the vertical component of the wind stress curl, the parameteris the deformation radius and β is the rate of change northward of twice the vertical component of the earth’s angular velocity. A is the eddy viscosity which is assumed independent of x and y. In the following we assume a rectangular ocean, extending from to =0x to =xr, and from =ys- to y=s. For boundary conditions, we assume that

Boundary conditions (2) state that the boundary itself is a streamline and that no slippage happens against the boundary. The initial condition is

We shall use the classical variable separation method to solve the initial boundary value problems (1)-(3). For this purpose we first consider the following Sturm-Liouville Equations for (1)-(3).

For the solution, it is assumed that the meridional structure of the solution is totally determined by the forcing term in the present paper. This is motivated by the work of Munk (1950). We assume that k is a constant. It is easy to see that the problems (4)-(5) has the following eigenvalues and eigen functions

Next we look for the solutions for problems (4)-(5) in the following formSolving the above ordinary differential equations, we find that

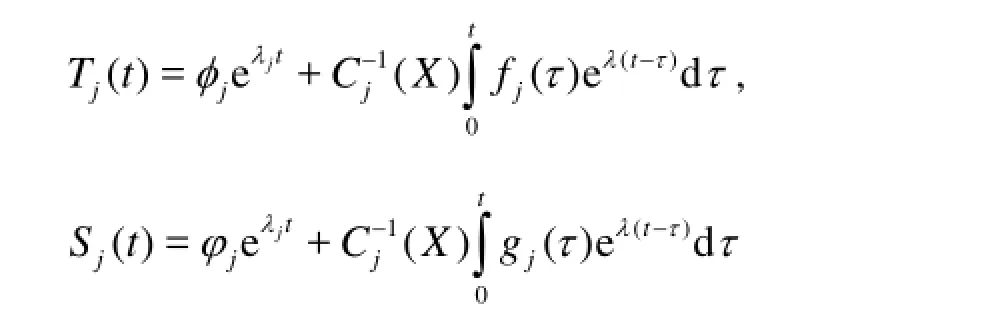
Thus, the solution of the problems (1)-(3) assumes the following form

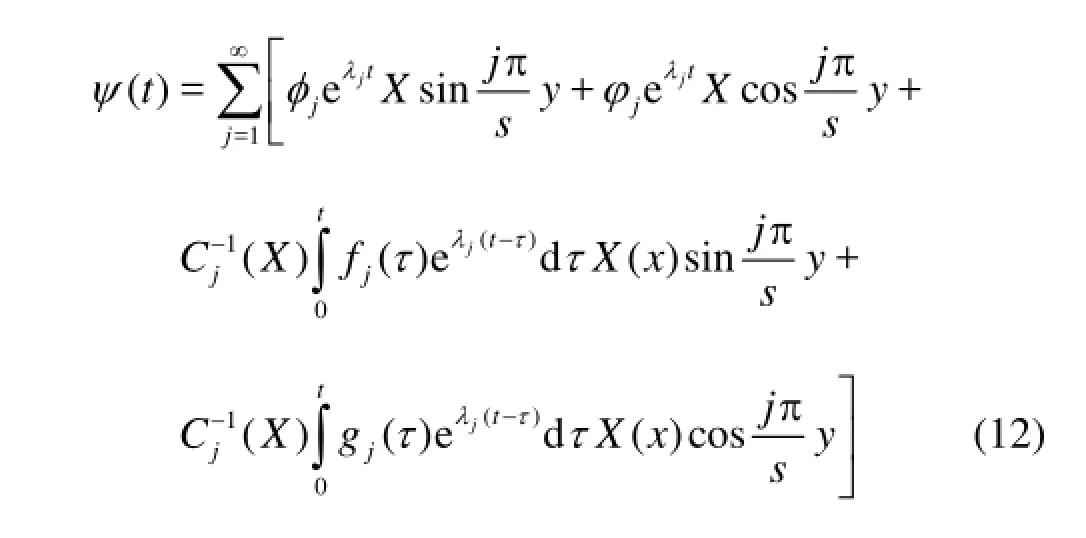
In the next section, we will make use of the analytic solution given in Eq.(11) to study the seasonal variation of the NECbifurcation.

2. Seasonal variation

We shall make use of the Florida State University wind data from 1961 through 1992, where the observed seasonally fluctuating wind stress curl field can be well represented by the following function

Approximately, we choose M =0.19×10-7Nm-3, B=3M and L=26.667o. Furthermore, we assume here that s=L. In view of problem (10), we note that

the following formula for the bifurcation latitude Yb(t) as the meridional velocity component is zero along the western boundary

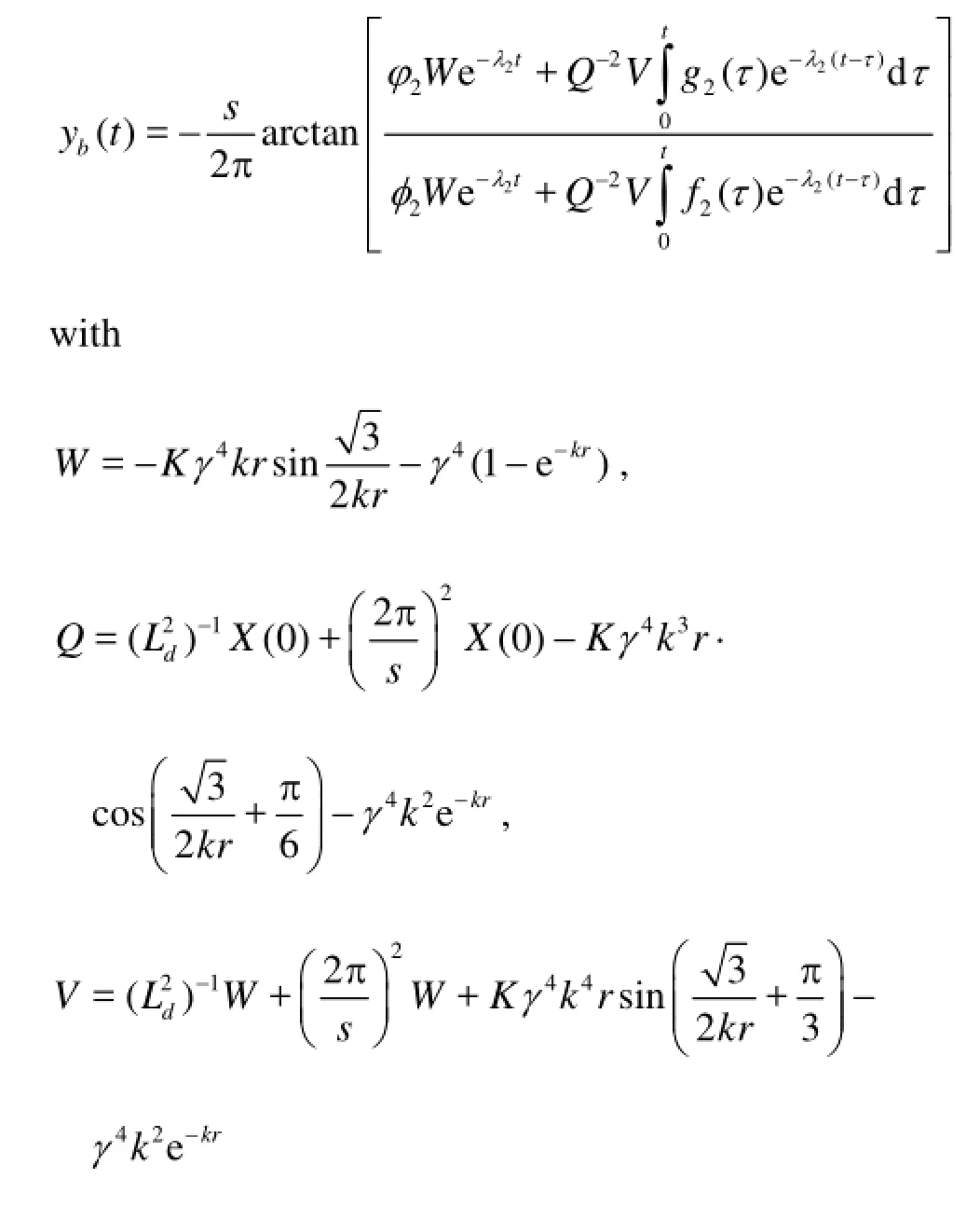
The stream function ψ(x,y,t) given in Eqs.(13) is depicted in Fig.1 for March, June, September and November. Yb(t) is depicted in Fig.2 to demonstrate the seasonal variation of the NEC bifurcation latitude. From Fig.2, we see that the NEC bifurcation is at its southernmost latitude (12.7oN) in June and the northernmost latitude(14.4oN) in November. It should be pointed out that the seasonal variation for the NEC’s bifurcation obtained here is very close to that obtained by Wang and Hu[8], who concluded that the NEC bifurcation is at its southernmost latitude (12.9oN) in June and its northernmost latitude(14.1oN) in December by analyzing the 12 year altimetry data from October 1992. It is noted that one could take initial data of zero. Then Fig.1 and Fig.2 would be those after the solution reaches the periodic state. It is also noted that the phase position of the bifurcation point for the NEC has 3 month’s delay compared with the phase of the wind stress curl field. It may be related to the propagation of the baraclinic Rossby wave. On the other hand, the wind field data used in the present paper are from the Florida State University wind data from 1961 through 1992. In fact, one could analyze the variability of the bifurcation of the North Equatorial Current by using the updated data and the solution constructed here. We shall continue this study in a future paper.

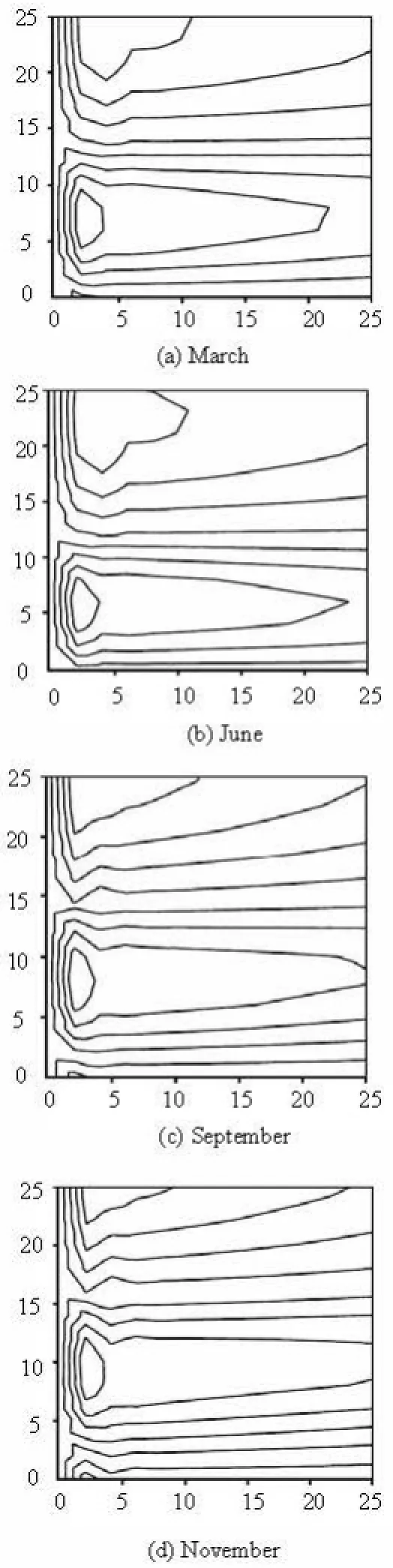
Fig.1 Stream functions in March, June, September and November

3. Conclusion

The variable separation method and the Munk’s (stationary) solution are used to construct the analytic solution of the time-dependent linear horizontal shallow water quasi-geostrophic equations. With the help of this analytic solution and the Florida State University wind data from 1961 through 1992, the seasonal variability of the bifurcation of the North Equatorial Current is investigated. It is found that the bifurcation of the NEC obviously changes its latitude with sea-sons. Furthermore, it is shown that the NEC bifurcation is at its southernmost latitude (12.7oN) in June and the northernmost latitude (14.4oN) in November. The results are very close to those given by Wang and Hu[8], who concluded that the NEC bifurcation is at its southernmost latitude(12.9oN) in June and its northernmost latitude (14.1oN) in December.

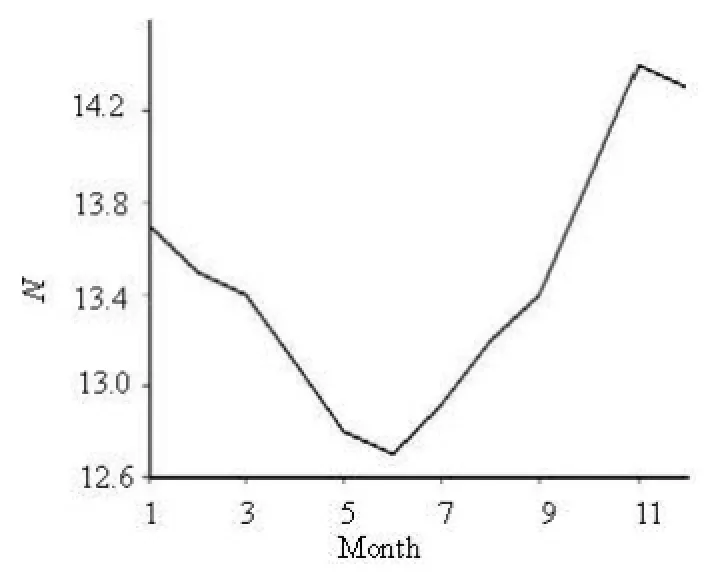
Fig.2 Seasonal variation of the NEC bifurcation latitude determined from Yb(t)

Acknowledgement

The authors would like to thank Prof. Hu Dunxin for many useful discussions, and thank the referees for helpful suggestions.

[1] ZHOU Hui, XU Jian-ping and GUO Pei-fang et al. Review on the west boundary current of the North Pacific Ocean[J]. Journal of Marine Sciences, 2006, 24(2): 49-59(in Chinese).

[2] CHEN Yong-li, HU Dun-xin. In fluence of heat content anamaly in the tropical western Pacific warm pool region on onset of South China Sea summer monsoon[J]. Acta Meteorologica Sinica, 2001, 17(Suppl.): 213-225.

[3] LÜ Lian-gang, QIAO Fang-li and YUAN Ye-li. Latitudinal variation of deep scattering layer in the western Pacific[J]. Journal of Hydrodynamics, Ser. B, 2004, 16(5): 571-581.

[4] WANG Fan, CHANG Ping and HU Dun-xin. Seasonal circulation in the northwestern tropical Pacific Ocean diagnosed with the assimilation data from 1989 through 1997[J]. Journal of Hydrodynamics, Ser. B, 2001, 13(3): 65-73.

[5] QU T., LUKAS R., The bifurcation of the North Equatorial Current in the Pacific[J]. Journal of Physical Oceanography, 2003, 33(1): 5-18.

[6] KIM Y., QU T. and JENSEN T. et al. Seasonal and interannual variations of the North Equatorial Current bifurcation in a high-resolution OGCM[J]. Journal of Geophysical Research, 2004, 109: C03040.

[7] LI Li-juan, LIU Qin and LIU Wei. Surface current speed and bifurcation of the North Equatorial Current in the Pacific Ocean[J]. Journal of Ocean University of Qingdao, 2005, 35(3): 370-374(in Chinese).

[8] WANG Qing-ye, HU Dun-xin. Bifurcation of the North Equatorial Current derived from altimetry in the Pacific Ocean[J]. Journal of Hydrodynamics, Ser. B, 2006, 18(5): 620-626.

[9] Wang Fu-jun, HU Dun-xin. A time-dependent baroclinic model on NEC bifurcation[J]. Chinese Journal of Oceanology Limnology, 2012, 30(1): 186-191.

[10] CUSHMAN-ROISIN B., BECKERS J. Introduction to geophysical fluid dynamics: Physical and numerical aspects[M]. Waltham, USA: Academic Press, 2011.

[11] WANG Qing-ye, CAO Rui-xue and ZHANG Shu-wen et al. Bifurcation of the north equatorial current in the upper layer of the Pacific Ocean[J]. Science China Series D: Earth Sciences, 2009, 39(1): 116-120(in Chinese).

[12] LIU Yu-long, WANG Qi and SONG Jun et al. Numerical study on the bifurcation of the North Equatorial Current[J]. Journal of Ocean University of China, 2011, 10(4): 305-313.

[13] MENG Qing-jia, WANG Fan and LIU Na. Low-frequency variability of the North Equatorial Current bifurcation in the past 40 years from SODA[J]. Acta Oceanological Sinica, 2011, 30(3): 14-19.

[14] WANG Fan, CHANG Ping and HU Dun-xin et al. A circulation in the northwestern tropical Pacific Ocean and its seasonal variation[J]. Chinese Science Bulletin, 2002, 47(7): 591-595.

[15] NI Guo-xi, JIANG Song and JU Qiang-chang et al. Nonlinear dynamical analysis of bifurcation and confluence of the Pacific western boundary currents[J]. Journal of Hydrodynamics, 2012, 24(3): 383-390.

10.1016/S1001-6058(11)60395-9

* Project supported by the National Natural Science Foundation of China (Grant Nos. 40890154, 40890153), the National Basic Research Development Program of China (973 Program, Grant No. 2005CB321700).

Biography: JU Qiang-chang (1976-), Male, Ph. D., Professor