关于振动采集设备频率分辨率的分析

袁 超 何 东 于光辉

(东方汽轮机有限公司， 四川 德阳， 618000)

关于振动采集设备频率分辨率的分析

袁 超 何 东 于光辉

(东方汽轮机有限公司， 四川 德阳， 618000)

频率分辨率是数字信号处理中一个重要的概念。在振动测试中，测试人员通常都希望收集到振动信号完整的特征信息，得到的频率、相位信息尽可能准确，频谱图中频率分辨率能够达到合适水平，但这些都与采集设备本身设计或者有关设置密切相关。 文章将就此展开分析， 并以 Bently 408 DSPI 为例说明如何设置才能得到合适的频率分辨率。

振动采集设备； 数字信号处理； 408 DSPI； 频率分辨率

0 引言

当前的振动测试，都是利用传感器将机械振动转换为相对应的模拟电信号，然后分析仪表对模拟电信号进行一系列处理，并从中提取受关注的信号特征值。对电信号的一系列常见处理包括：模拟信号调制、模数转换、数字结果计算处理（例如 FFT）、 获取特征值、 绘制相关图谱等。 而本文讨论的频率分辨率问题就和模数转换与数字计算过程密切相关。

1 信号采样

模拟信号就是自然界连续的信号。相反，数字信号就不是连续的，是离散的信号。从模拟信号到数字信号的过程称之为模数转换，也可以称作信号采样。图1为模拟信号示意， 而图2为同一信号的数字化表示。

图1 典型模拟信号的时域波形

图2 模拟信号数字化后的时域波形

对模拟信号数字化的质量取决于两个因素：幅值分辨率 （垂直轴） 和时间分辨率 （水平轴）。幅值分辨率由分析仪表的模数转换器 （ADC） 位数控制； 时间分辨率由采样率控制[1]。 采样率是指单位时间内将模拟样本数字化的数量，数字化的样本数量越多，则采样率高，否则采样率低。Bently 408 DSPI的最高同步采样频率为 32kHz。

根据采样定理 （奈奎斯特定理）， 在进行模拟/数字信号的转换过程中， 当采样频率 fs大于信号中最高频率 fmax的 2 倍时 （fs≥2fmax）， 采样之后的数字信号完整地保留了原始模拟信号中的信息。

2 频率分辨率

频率分辨率是指所用的算法能将信号中两个靠得很近的谱峰保持分开的能力[2]。 实际应用时， 可以将频率分辨率理解为频谱图中，在频率轴 （频谱图的水平轴）上得到的最小频率间隔。

如果采样频率为 fs， 采样时间间隔为 ts， 采样点数为N， 采样时间为 t （完成一组样本的采集所需要的时间）， 则频率分辨率△f为：

这里△f的单位是 Hz， t的单位为 s。 也就是说， 一组样本采样时间越长 （t越大）， 频率分辨率越高 （△f越小）。

但实际使用振动采集设备时，通常不能直接配置采样时间 t， 而是配置每周期采样点数或（和） 采样周期数等信息。 两者的关联以 408 DSPI为例进行说明。

旋转机械产生的振动信号为周期性信号，振动采集设备对信号处理时大多采用 FFT 运算， FFT运算要求一组样本的采样点数为 2n， 所以通常一组样本采样点数为 1024 或 2048 等。 408 DSPI要求每次进行的数据分析的样本采样点数为 2048，即 N=2048。

根据文献[3]介绍： 采样频率 （Hz） =转速 （r/ s） ×每周期采样点数 （Samples/r）。 则对 408 DSPI而言， 式（1）可以变形为：

从式（2）可以看出：

（1） 转速一定时， 频率分辨率与每周期采样点数 （Samples/r） 呈线性关系， 每周期采样点数越多， 频率分辨率越低 （△f越大）。 反之， 频率分辨率越高 （△f越小）。

（2） 配置好每周期采样点数， 频率分辨率还与转速呈反比例关系。对汽轮机振动数据采集而言，不同的转速，对应不同的频率分辨率，且转速越高时，频率分辨率越低。

由于 408 DSPI每次进行数据分析的样本采样点数固定为 2048， 所以设置不同的每周期采样点数， 即得到对应的采样周期数 （2048/每周期采样点）。所以转速一定时，采样周期数确定采样时间，每周期采样点数越少，采样周期越多，采样时间越长， 从式（1）可知， 频率分辨率越高。

若固定了每周期采样点数，即固定了采样周期数。然而固定的采样周期数在不同的转速条件下，采样时间也会不同。转速越高，采样时间越短， 从式（1）可知， 频率分辨率越低。

换个角度分析， 前文已经提到 408 DSPI每次计算 2048 个数据点 （一组样本）， 即一次 FFT 运算分析 2048 个数据。 根据分析结果绘制频谱图，图中有 1024 谱线， 频率分辨率即为两谱线间的频率间隔。 所以， 如果确定了 1024 谱线对应的频率范围，就可以得到频率分辨率。

由采样定理可知， 当采样频率 fs大于信号中最高频率 fmax的 2 倍时 （fs≥2fmax）， 模拟信号可以被还原。即当采样频率确定时，频谱中的频率范围就可以确定。 由于 fmax≤fs/2， 所以 fmax的最大值就是 fs/2， 频率范围就是 0～fmax（Hz）， 频率分辨率可以表示为：

式（2）和式（3）表达完全一致。

3 算例

从式（2）或式（3）可知， 进行振动数据采集时，为了得到合适的频率分辨率，在采集设备上可通过设置每周期采样点数达到要求。

前文已提到， 408 DSPI振动采集设备的最高同步采样频率为 32kHz， 且每次分析 2048 数据点。 最高同步采样频率为 32kHz即是说采样最快能够达到 32000 （Samples/s）， 如果设置 408 DSPI测试的最高转速为 10000 （r/min）， 则有 （32000× 60） /10000=192 （Samples/r）。 即在当前设置条件下， 408 DSPI最快每周期可以采集 192 个数据点。

另外， 408 DSPI每次分析 2048 数据点， 即2048=每周期采样点数×采样周期数， 而 2048=211，所以每周期采样点数和采样周期均应为 2n。 而 192不是2的整数次幂，所以上文的设置中，最大每周期采样点数应该取 128 （27， 小于 192 的最大 2的整数次幂）。 408 DSPI中实际配置情况如图3 所示。

图3 408 设置示例 1

图4 408 设置示例 2

同理， 图4 中， 当设置 408 DSPI测试的最高转速为 6000 （r/min） 时， 最大每周期采样点数应该取 256。

针对图3 中示例 1 的设置， 2048=128×16， 即每周期采集 128 数据点， 连续采集 16 周期进行分析。 则通过式（2）或式（3）计算， 3000r/min 时最高分析频率为：

所 以 频 率 分 辨 率 应 为 3200/1024=3.125Hz。408 DSPI中实际情况见图5 （3.13Hz）。

图5 示例 1 设置下， 转速 3000r/min 的频率分辨率

相同采集设置下， 2120r/min 时最高分析频率为 2261Hz， 所以频率分辨率应为 2.208Hz， 950r/ min 时最高分析频率为 1013Hz， 所以频率分辨率应 为 0.989Hz。 408 DSPI 中 实 际 情 况 见 图6（2120r/min 的频率分辨率 2.21Hz） 和图7 （950r/ min 的频率分辨率 0.99Hz）。

图6 示例 1 设置下， 转速 2120r/min 的频率分辨率

图7 示例 1 设置下， 转速 950r/min 的频率分辨率

国内某公司生产的振动分析装置采集设置为每周期采集 64 点， 采集 16 周期进行 FFT 分析，分析点数为 64×16=1024 （频谱图为 512 线）。 如此设置下， 通过式（2）或式（3）计算， 3000r/min 时最高分析频率为 1600Hz， 所以频率分辨率应为1600/512=3.125Hz。

以上算例中， 3000r/min 时的频率分辨率均为3.125Hz， 频率分辨率较低， 不满足实际分析需要。 3000r/min 为汽轮发电机组工作转速， 为满足在该转速上的分析需求，需要测试系统具有更高的频率分辨率。 所以建议在 408 DSPI中设置每周期采样点数为 32。

如此， 则有 2048=32×64， 即每周期采集 32数据点， 连续采集 64 周期进行分析。 则通过式（2）或 式 （3） 计 算 ， 3000r/min 时 最高 分 析 频 率 为800Hz， 所以频率分辨率应为 800/1024=0.78125Hz（小于 1Hz）。 并且随着转速降低， 频率分辨率会更高，完全满足分析、诊断需求。

图8 和图9 分别是 408 DSPI每周期 128 点和32点设置下， 同一信号的频谱图。 可以明显看出，配置每周期采集 32 点时 （采样时间较长）， 频率分辨率更高。

Epro MMS6000 系统中， 也有类似配置， 保证信号测量的频率分辨率， 如图10。

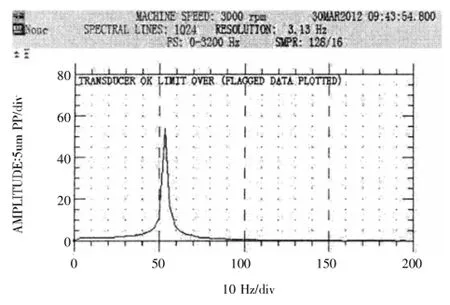
图8 每周期采集 128 点的频率分辨率

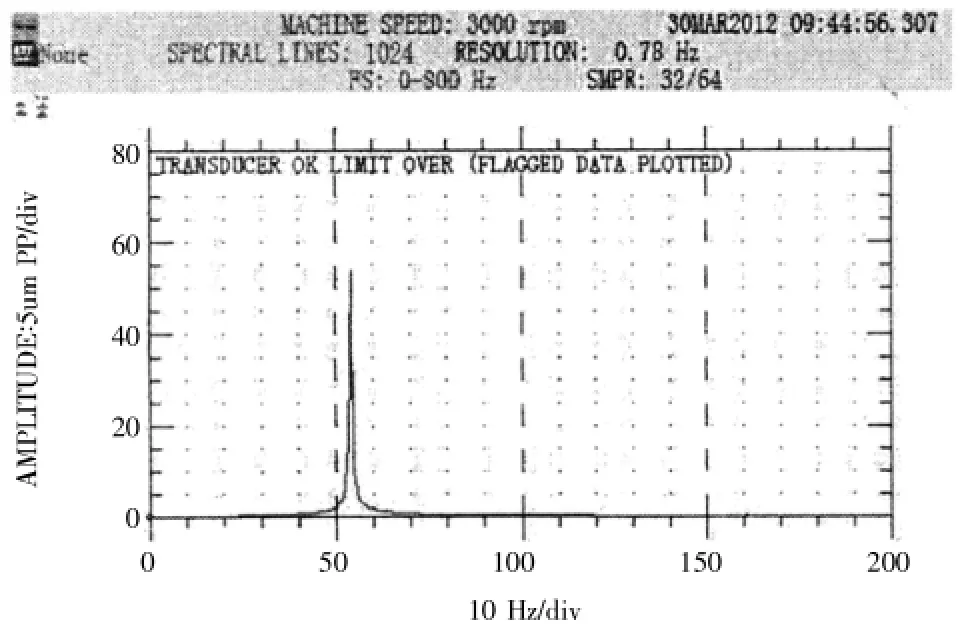
图9 每周期采集 32点的频率分辨率

图10 Epro MMS6000 采样配置

4 总结

（1） 信号采集时间越长， 频率分辨率越高。

（2） 固定分析数据样本点后， 可以通过改变每周期采样点数调整设备采样时间，进而改变频谱分辨率。

（3） 配置采样参数后， 频率分辨率与机组转速成反比例关系。

（4） 对 408 DSPI而言， 测量汽轮发电机振动时， 配置每周期采集 32点可以得到合适的频率分辨率。

（5） MMS6000 系统中可用相同原理分析。

[1]Gaston Desimone.ADRE 408 DSPi signal progressing[J]. Orbit,2011,31（3）:40-54

[2] 王刚,王艳芬,等.关于离散傅里叶变换频率分辨率的讨论[J]. 电气电子教学学报,2006,28（6）:18-20,24

[3]ADRE 408/Sxp Training M anual

The Analysis for the Frequency Resolution of Vibration Data Acquisition Device

Yuan Chao， He Dong， Yu Guanghui
（Dongfang Turbine Co.,Ltd.Deyang Sichuan 618000）

The frequency resolution is an important concept in the digital signal processing.In the vibration testing,testers always hope to get complete feature information,and gain exact specifics about frequency and phase,and obtain appropriate frequency resolution.Butall the information is closely related to the design or setting of acquisition device.This article analyzes the design or setting,and points out how to get appropriate frequency resolution by different setting in Bently 408 DSPI.

vibration data acquisition device,digital signal processing,408 DSPI,frequency resolution

袁超 （1985-）， 男， 重庆人， 2007 年毕业于北京科技大学应用物理系， 获理学学士， 现从事汽轮发电机组振动故障诊断及现场平衡工作。