风电对储能电池的计算和选取方法

禹争光 郑 谦 薛慧婷 杨德存

(东方汽轮机有限公司， 四川 德阳， 618000)

风电对储能电池的计算和选取方法

禹争光 郑 谦 薛慧婷 杨德存

(东方汽轮机有限公司， 四川 德阳， 618000)

文章以某风场 1.5MW 风机风能数据为例， 首先通过建立数学模型和指数加权移动平均值算法， 统计分析时间常数对于平滑电能的关系，获取较佳的时间常数值，然后对风电配套存储电池的电池功率与电池容量进行计算分析。最后给出最佳电池功率和容量的判据原则。

风电能；功率波动；模拟计算；电池功率和容量

0 引言

随着风力发电成本降低和技术日趋成熟，近年来国内风电场的建设也呈高速发展趋势。然而，因风电电能输出受天气、地理条件、气流紊流和风机塔影效应等因素影响，风电能量输出具有很大的间断输出和波动特性。由于风电的波动、随机和间歇等不利特征， 电网调度 （发电） 不能准确地对系统内风电场出力进行预测和相应调整，导致上网风电输出对电力系统的安全性与稳定性造成很大的影响[1]， 这在很大程度上制约了风电应用的快速发展[2]。 所以， 促进风能的利用与发展，减小风电的输出波动具有重要意义，而储能技术是平滑风电输出和抑制电压闪变的一种较佳方法[3]。在使用储能平滑输出时，需综合考虑成本，储能容量的选取时就必须考虑输出电能平滑程度和储能成本相互关系，从而获得较佳数值。

在平滑风电电能输出研究中，配套电池容量选择是风电应用研究中的关键课题，这需结合风电系统—电网电能输出目标设定、风场现场数据以及储能技术成本等综合考虑而定[4]。 在电能平滑理论分析模型研究方面，国外研究提出了系列相关理论模型和平滑算法[5]。 本文依据某风机采集数据为计算依据，建立离散低通滤波模型，采用指数加权移动平均值算法，通过计算机仿真来获取最佳电池功率与容量。

1 平滑输出模型计算

对风电输出的电能平滑效果分析中，普遍采用两个评估指标[6]： 风电输出的标准偏差； 输出波动变化率。

（1） 标准偏差

标准偏差表征一个电能输出稳定度，用来评估长时间内风电输出波动的指标，其数值在风电上表现为不确定性，随风场地址、时间段改变而变化。采用标准偏差可以衡量一个随机变量偏离它的均值程度。若输出能量曲线越平坦，标准偏差越小，表征随机变量偏离均值越小。

（2） 输出波动的变化率

输出波动的变化率是一个评估短时间段内风电输出波动的评估指标，平滑波动的变化率为相邻两输出差的绝对值，可采用变化率平均值和均方差来表征。

1.1 风电能统计分析

本次计算数据以某风机 （额定功率 1.5MW） 1个月期间 （2011 年 5 月 20 日～2011 年 6 月 19 日）运行的功率数据为基础。单点数据采集时间间隔为 10min， 风电功率所测数据如图1 所示。 通过统计计算得知： 平均输出功率 278.5kW， 其电能输出分布结果如图2所示。 由图2可知： 其中超过66%时间概率时功率输出值低于 1/5 额定功率值，而 超过 1200kW （ ＞80% 额 定功 率） 概率 仅有1.22%， 广义数据样本基本呈正态分布。

图1 风机一个月功率输出数据图

图2 风能输出功率统计图

图3 是计算得到风电功率输出的波动图。统计分析可得：1个月内功率波动最大值：1236.29kW， 平均值： 64.21kW， 均方差： 102.28。由于不同风场和风机具有不同的风力和风机特性，其输出电能相差各异，所以每次计算都需要先进行风电出力特性的研究，获得最佳电池容量的选取。

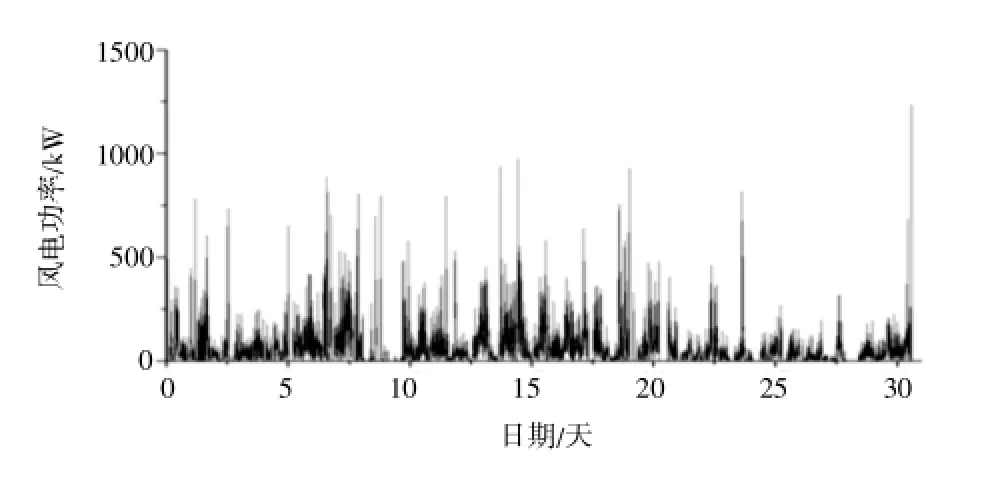
图3 风机一个月功率波动图

1.2 平滑时间常数选取

在离散低通滤波模型中，平滑时间常数大有利于风能数据输出波形的平滑度和减小输出标准偏差，但选用大的平滑时间常数值却会提升对储能功率和容量的需求而增大储能设施的成本。所以，必须综合考虑，通过平滑电能质量的极值点计算，选取较佳的平滑时间常数。

本数据样本是以时间间隔 600s （10min） 采样的离散数据，对此，可建立离散低通滤波模型。分别预先假设 5 组平滑时间常数（s）： 600、 1200、2400、 5000 和 10000， 然后采用指数加权移动平均值算法求解。 为便于表示， 以 2011 年 6 月 5 日为例，上述5组平滑常数下电能输出曲线效果如图4所示。

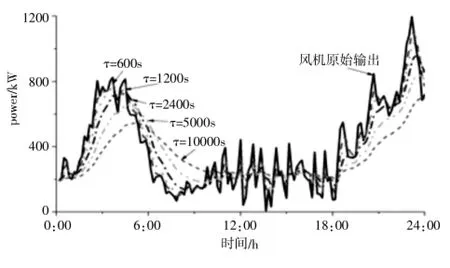
图4 不同时间常数下风能平滑效果关系图（时间常数=600， 1200， 2400， 5000， 10000）

图5 时间常数与波动率关系

明显可见，随着时间常数增大，平滑效果提高。 但相比于采用 600s和 1200s数据曲线， 后期的增大平滑效果已不如先前明显。通过进一步波动的平均值和均方差分析 （见图5）， 可以发现：平滑时间常数在 2400s时， 平滑效果随时间常数变化已趋缓，波动率平均值和均方差分别已下降73.9%和 77.8%， 可选用为本风电输出较佳的时间常数值。 本例以 2400s作为电池容量计算基础。

1.3 电池容量计算

图6 是采用时间常数为 2400s时， 电池在 1个月充放电状态计算模拟数值。 采用 95%输出功率置信率和系统平滑稳定误差率1%计算模拟数据样本得到： 电池功率需要： 296.5kW， 电池容量数值为： 675.82kW·h。 若考虑电池系统运行效率等于 70%， 则电池容量应选择为： 795.11kW·h。 故针对本例风机储能电池选取 300kW， 储能容量800kW·h， 即额定功率的 1/5 和 2.67h 的储能容量。

图6 2400s时间常数电池充放电状况

在 2400s为时间常数时， 通过计算， 其风电电能输出标准偏差下降 15.9%。

1.4 计算讨论

通过计算发现： 若采取 100%输出置信水平或误差率等于0， 将会成倍增加对电池功率和容量的需求，极大增大储能系统成本。所以，根据电网需求[7]和风场配置情况， 合理设置置信水平和误差率，是比较切合实际的选取方式。

实际选用时，时间常数和电池容量计算是一个反复计算过程，本文主要介绍计算思路和算法，省略了部分具体计算步骤。

2 结论

通过风机现场等间隔采集数据为分析样本，采用离散低通建模、指数加权移动平均值数学计算和统计分析，得到对储能电池功率、容量的较佳数值。表明该算法和选取方法对风机、风场中储能电池容量和功率选取具有指导性。通过本例1.5MW 风机一个月采集的样本数据， 计算得到电池功率较佳选择在 300kW， 容量 800kW·h， 可实现风电电能输出标准偏差下降 15.9%平滑输出。

[1] 迟永宁.大型风电场接入电网的稳定性问题研究 [D].北京： 中国电力科学研究院， 2006

[2] 曾鸣,沈又幸,吕俊昌.基于空间平滑法的风电场短期出力预测模型 [J]. 现代电力,2008,25(3):81-84

[3]C.Abbey,G.Joos.Supercapacitor energy storage for w ind energy applications[J].IEEE T rans.Industry Applications, 2007,43(3):769-776

[4] 肖珉,尚小林,白卫,等.风光互补储能发电系统并网技术研究 [J].东方电气评论,2012,26(101):56-59

[5]J.P.Barton,D.G.Infield.Energy storage and itsuse w ith intermittent renewable energy[J].IEEE Trans.Energy Convers.,2004,19(2):441-448

[6]Jukka V P， Peter D L.Effect of energy storage on variations in w ind pow er[J].W ind Energy,2005,8(4):424-441

[7] 中华人民共和国国家质量监督检验检疫总局.中华人民共和国国家标准化指导性技术文件,GB/Z 19963-2005.风电场接入电力系统技术规定 [S]， 2006

Methods of Selection and Calculation of the Storage Battery forW ind Power

Yu Zhengguang， Zheng Qian， Xue Huiting， Yang Decun
（Dongfang Turbine Co.,Ltd.Deyang Sichuan 618000）

This paper presents the relationships between the time constant and smoothed output of power fluctuations,based on low-pass filtermodel and the algorithms of exponentially weighted moving average filter (EWMA).Moreover,by taking the data of 1.5MW wind turbine generators for example,we make the calculation of optimal storage battery power and capacity for power fluctuation.Meanwhile,the procedure and principle for the choose of energy storage battery have been proposed.

wind energy,power fluctuation,computational simulation,battery power and capacity

禹争光 （1970-）， 男， 工程师， 2005 年取得电子科技大学微电子与固体电子博士学位， 现从事新能源技术研发工作。