三维离子阱内空间电荷效应的理论分析

张 华，张小华，肖瑞林，丁传凡

（1.北京普析通用仪器有限责任公司，北京 101200；2.赣南师范学院物理系，江西 赣州 341000；3.复旦大学化学系激光化学研究所，上海 200433）

质谱仪是用于检测和分析各种物质成分的科学仪器，是目前进行化学和生物分析的最主要仪器之一［1－4］。质谱仪已经成为许多领域的必备分析仪器，被广泛地用于物理、化学、环境保护、医药卫生、地质、天文等领域［5－8］。离子阱质谱具有体积小、结构简单、使用方便等优点，已被广泛应用于许多领域。它除了具有常用的质量分析功能外，还可进行离子的串联质谱质量分析，获得更多有关分子结构和构型的信息。三维离子阱由于具有比线形离子阱更小的体积，近年来已成为小型化质谱的首选。同时，由于三维离子阱具有较小的结构和体积，其阱内离子的存储空间也比线形离子阱小得多，因此，当三维离子阱进行离子存储和质量分析时，其大量带电离子之间的库仑相互作用（即空间电荷效应）是影响离子阱质谱获得高质量精度、高质量分辨以及高灵敏度分析的瓶颈［9－21］。在实际应用中，一般是采用所谓的预扫描方法将离子阱中的离子先逐出一部分，即通过减少阱中离子数量的办法来减小空间电荷效应。很显然，这与实现样品的高灵敏度分析是背道而驰的。理论上，由于离子阱内存在的离子数量成千上万，对于这样一个多体问题，目前还很难建立一个清晰的物理模型，数学上也很难给出准确的分析解。

本工作根据三维离子阱内的离子分布情况，假设离子在三维离子阱的中心区域呈近似于球对称的高斯分布，通过求解阱内电场所对应的电势函数满足的泊松方程，得到这个球对称高斯分布的离子云所产生的电场解析表达式。进一步在小振动近似下，得到离子的久期（secular）频率与阱内离子数目的理论关系。

通过应用Mathematica数学模拟软件，计算模拟不同久期运动频率的离子在不同个数的离子所组成的离子云排斥作用下的久期主频率的移动。

1 理论计算模型

在理想的三维离子阱质量分析器中，其离子阱电极的空间几何结构是由一个环电极与一对端盖电极所构成。在柱坐标系｛r，z｝中，电极的几何结构满足简单的数学方程［22］。

环电极是一个绕z旋转双曲面，其母线满足一个双曲线方程:

其中，r0是环电极内表面所在圆周的半径。

前后端盖电极也是旋转双曲面，其母线满足另外一个双曲线方程:

其中，2z0是2个端盖电极之间的最短距离。

为了产生完美的四极电场，当用环电极与一对端盖电极组成一个四极质量分析器时，它们之间的空间相对位置还需要满足一定的几何约束，即:

一个可以产生完美四极场的三维离子阱在对称平面上的截面图示于图1。

一个三维离子阱在工作状态下，其工作电压的施加方法为在环电极上加载一个射频电压:

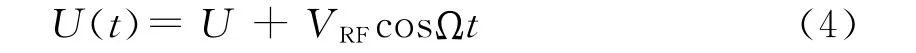
式中，U 为直流电压，VRF为交流射频电压。

图1 三维离子阱的几何结构截面图Fig.1 Crosssection view of 3Dion trap

端盖电极一般为接地，或偏置一定的直流电压。这样将在离子阱内部产生一个随时间变化的四极电场。

根据库仑定律，带电粒子在四极电场中将受到电场力的作用。离子在电场力作用下的运动满足牛顿第二定律。

根据F＝ma，可得离子在z方向的运动方程为:

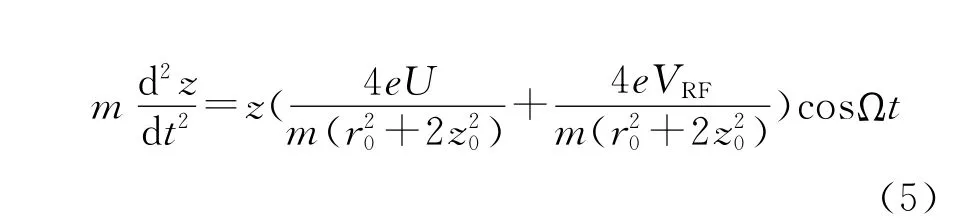
其中，e为离子所带的电荷电量。

方程（5）是通常所说的描述离子在四极电场中运动的马修方程。此方程的求解过程比较复杂，这里不做详细讨论，可参考文献［23］。

方程（5）可以写成以a和q为参数的标准马修方程，其稳定性参数β可以计算出来。比如，当a＝0，q＝0.6537时，β＝0.5144；当a＝0.2353，q＝0.2615时，β＝0.5310。其中，a与q是四极场第一稳定区的稳定三角形上的坐标，它们还分别对应环电极上所加的直流电压U和射频电压的大小。在这个运动方程中，离子的运动比较复杂，数学上可以解析成是由许多不同频率运动的加和。其中，离子振动的频率为:

式中:n＝0，±1，±2，…；β是与ax，qx相关的函数。

n＝0时的频率被称为久期频率。久期频率是最重要的运动频率，离子在三维空间中类似于李萨如图象的复杂运动，其主要运动模式是简谐振动，为了简洁，假定这个简谐振动正好沿着径向，这样运动只有r这个自由度。事实上，不论简谐振动的方向是如何变化，它在径向上的分量也一定是简谐振动，所以上述虽然是很强的假定，但不影响计算结果的适应性。

在这个前提下，可以把三维空间内的复杂运动约化为一维运动:

如果考虑三维离子阱内空间电荷产生的电场¯E，则离子运动还同时受到电场力¯Eq的作用，其运动方程将变成如下形式:

在质谱仪中，决定离子运动的是电场，该电场所对应的电势在真空下满足拉普拉斯方程［23］，它是一个椭圆型的线性偏微分方程。离子阱的机械结构，即电极的空间位置决定了这个偏微分方程的边界条件。数学上，当边界条件给定后，偏微分方程将具有唯一的解。在有空间电荷效应的情况下，离子在离子阱内电场中的运动满足泊松方程，即:

为了求解（9），假设在离子阱内离子的电荷密度分布近似于球对称，所以可以选择球坐标系来求解方程。

假设离子阱内的离子云电荷密度为高斯分布，因此有:

对全空间积分，即可以得到离子阱内离子的总电量Q。

球对称电势的解析表达式为:

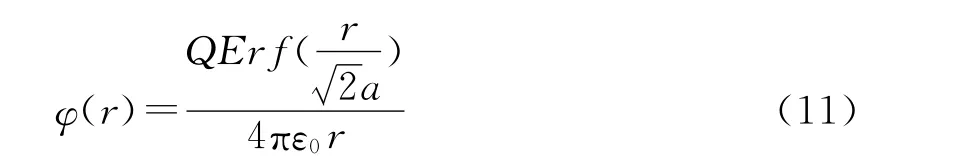
其中，Erf为误差函数。

对式（11）做微分，可以得到r方向的电场强度。考虑到球对称性，电场只有r方向的分量，即:

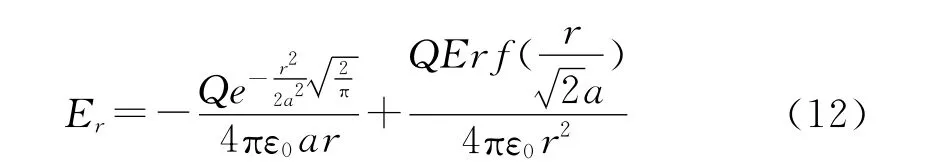
所以，考虑在r方向做久期运动的离子，当它受到电场作用时，其运动方程为:

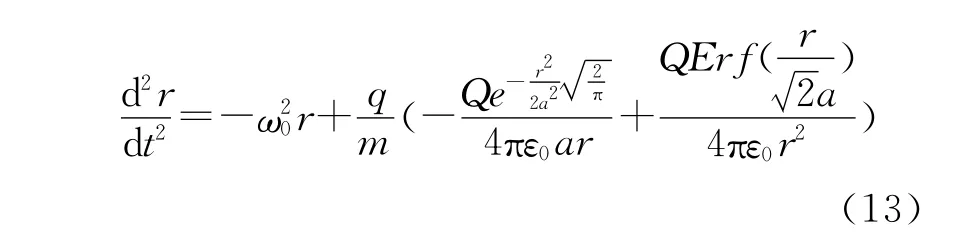
在r＝0附近做泰勒展开，可以得到小振动近似。对展开结果取二级近似（即前2项），得到以下的非线性振动方程:

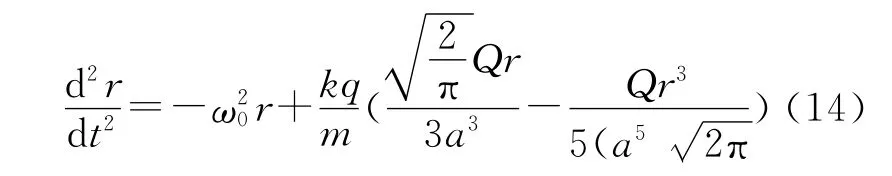
因为非线性的三次项在r远远小于a的小振动近似下是小量，可忽略，得到r远远小于a时的小振动近似下一级修正后的频率为:

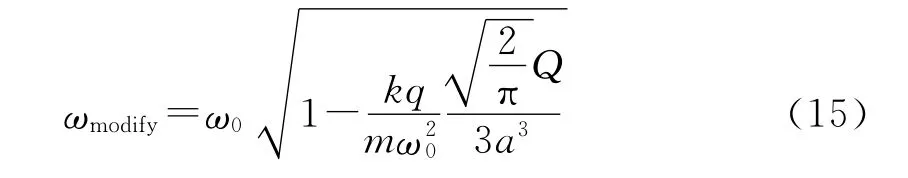
总电量Q等于N个单位电荷所带电量的总和。

根据以上分析，可以得到频率移动与离子个数N的关系式为:

其中:k是库仑常数；m是离子的质量；q是离子所带的电荷；Q是产生空间电荷效应的离子总电量；a是离子云大小的典型几何尺寸，它往往是由离子阱的几何尺寸决定的；ω0是没有受到空间电荷效应影响时的离子运动频率；N是离子云中离子的个数（假设每个离子都只带有单位电量，即为单电荷离子，对多电荷离子，其离子个数与电荷数的关系很容易求得）。

可以看到，在r远远小于a的小振动情况下，一级近似结果式（16）与数值模拟符合得较好。

2 理论计算结果

根据以上讨论的物理模型和在一定的近似下所得到的离子在离子阱内的运动方程，可以计算离子阱内的空间电荷效应对离子运动久期频率的影响。

根据式（16）计算得到的结果示于图2。计算中所选定的相关参数为:

离子质量m＝100×1.67×10－27kg；

离子阱内的球形离子云直径a＝0.001m；

离子所带电荷q＝1.6×10－19C；

离子久期运动频率ω0＝350000Hz。

由图2可以看出，离子久期运动的频率随着离子阱内离子个数的增加而减小。也就是说，由于空间电荷效应的影响，离子在离子阱内的运动会发生变化。如，在离子云分布尺寸为1mm的三维离子阱中，固有久期频率为350000Hz的离子，随着离子阱中离子个数的增加，离子做久期运动的频率下降，当离子云中离子的个数接近33万个时，离子的久期运动频率趋于零。

很显然，离子在离子阱内的运动频率是不可能为零的。计算结果与实际情况的偏差主要有以下方面的原因:首先，目前的实验结果表明，一般三维离子阱内所能存储的离子数可至数万个，但很难达到几十万个，很小体积内大量离子间的库仑相互作用力，即大量相同电荷间的排斥力，将使得离子阱内可以稳定存在的离子总数有一个上限，这个上限一般在几十万以内；第二，建立物理模型时对离子云分布情况的假设，如球形对称、高斯分布和离子云大小等；第三，计算过程中的近似处理，如小振动近似、泰勒展开近似等。但计算结果对于理解空间电荷效应对离子运动的影响仍然是有意义的，它为进一步建立更切合实际情况的离子阱物理模型和数学求解提供了有价值的参考。

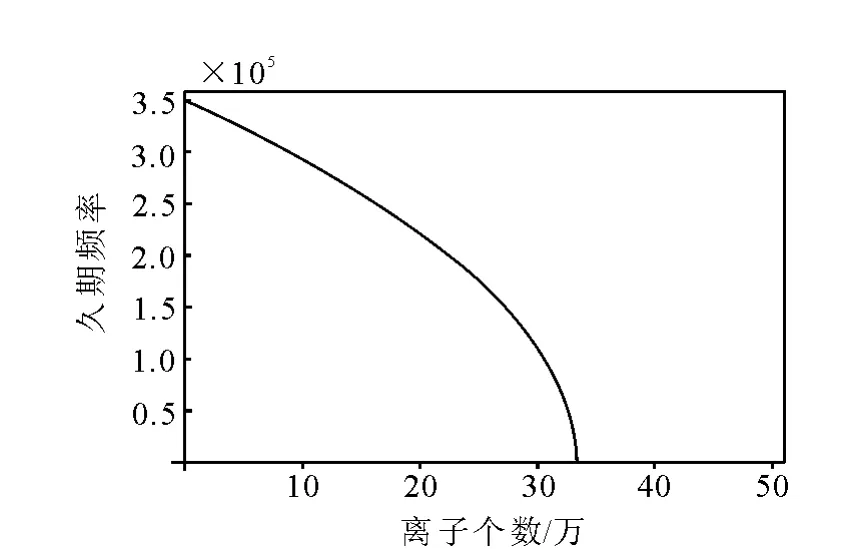
图2 三维离子阱内离子运动的久期频率与离子个数的关系Fig.2 Relationship between secular frequency and ion number in 3dion trap

3 数值计算结果

为了比较所建立的离子阱物理模型以及根据这个物理模型所做数学分析的结果的可靠性，还对离子阱内离子之间的空间电荷效应进行了数值计算分析。

对离子在阱内的运动轨迹，编写了mathematica程序，并在离散傅里叶分析的基础上进行了数值计算分析。

对于离子初始条件和离子阱工作参数如下的离子，可以得到其运动的久期频率与离子阱内离子总数的关系，即空间电荷效应对离子运动久期频率的影响。

为了便于比较，仍然取以下参数:

离子质量m＝100×1.67×10－27kg；

离子阱内的球形离子云直径a＝0.001m；

离子所带电荷q＝1.6×10－19C；

离子久期运动频率ω＝350000Hz；

离子数N＝10000。

理论计算结果显示，在上述条件下，当离子阱内存在10000个离子时，质荷比为100的单电荷离子的运动基本频率由ω0＝350000Hz变为ωmodify＝344718Hz，示于图3。

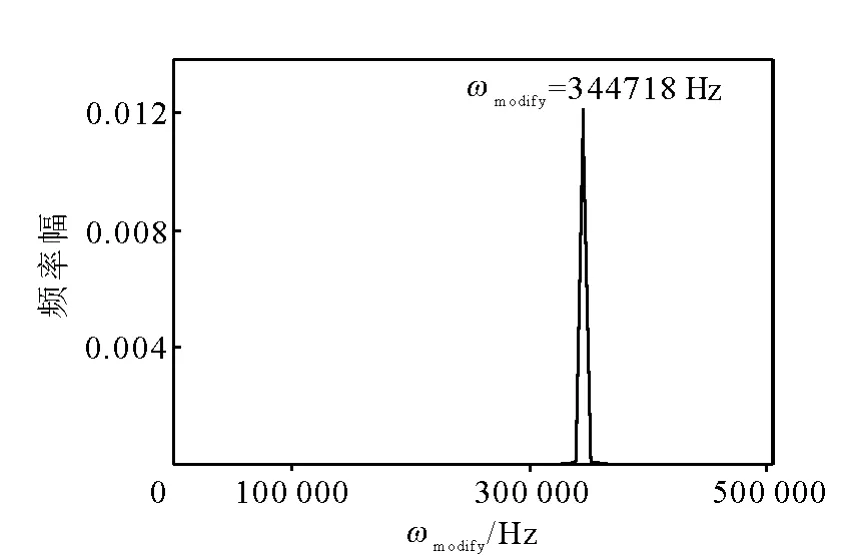
图3 350000Hz离子久期频率的频率移动到344718HzFig.3 350000Hz secular frequency shift to 344718Hz

前面给出的数值解结果是ωmodify＝344654Hz，与这里的结果非常接近。

由此可见，根据式（16）得到的理论数值，与通过离散傅里叶变换得到的离子轨道频率谱的数值解基本一致。

对于其他不同离子个数所产生的空间电荷效应，通过改变mathematica程序中的参数计算，对离子轨迹做离散傅里叶分析，研究其频率谱发现，式（16）可以很好的给出频率移动的表达式。

通过比较，使用式（16）计算所得到的结果与使用mathematica程序做数值计算所得结果非常接近，列于表1。说明所建立的物理模型和数学方法与实际情况具有很好的一致性，理论计算方法和结果可以作为实验参考。

表1 在空间电荷效应的作用下，离子运动的久期频率改变与离子阱中离子数目的关系Table 1 The relationship between the frequency shift of ion secular motion and the number of ions in the trap

4 结论

本工作研究表明，可以在一定的近似下建立离子阱内离子运动的物理模型，并根据这个模型建立有空间电荷效应情况下的描述离子运动的数学表达式。通过解析求解近似条件下的离子运动方程，给出离子运动的久期频率与空间电荷（离子云内包含的离子个数）的关系。

通过进一步使用自编的mathematica程序，对离子的运动轨迹做离散傅里叶分析，同样可以得到离子运动久期频率的变化数值解。

上述两种不同方法（近似条件下的解析解与数值解）所得到的结果基本一致。说明本工作所给出的描述离子阱内离子运动的物理模型及数学表达方法基本可靠，这为进一步建立更准确的离子阱物理模型，求解离子在离子阱内的运动状态具有重要的参考价值。

由于在三维离子阱中，空间电荷效应是造成质谱峰偏移和仪器灵敏度下降的重要因素之一，从理论上准确理解离子阱内离子数量与离子运动状况的关系，对进一步理解离子阱质谱的工作原理，改善离子阱质谱仪的性能都具有参考价值。本工作将根据实验结果不断改进，以建立能够准确描述离子阱质谱，包括三维离子阱、线形离子阱的物理模型。

［1］De LAETER J R.The role of mass spectrometry in atomic weight determination［J］.Mass Spectrometry Reviews，2009，28（1）:2－19.

［2］BIAN Q，FORBES M W，TALBOT F O，et al.Gas－phase fluorescence excitation and emission spectroscopy of mass－selected trapped molecular ions［J］.Phys Chem，2010，12（11）:2590－2598.［3］GUNA M，LONDRY F.Tandem ion trap design with enhanced mass analysis capabilities for large populations of ions［J］.Anal Chem，2011，83（16）:6363－6367.

［4］SECOND T P，BLETHROW J D，SCHWARTZ J C，et al.Dual－pressure linear ion trap mass spectrometer improving the analysis of complex protein mixtures［J］.Anal Chem，2009，81（18）:7757－7765.

［5］SCHWARTZ J C，SENKO M W，SYKA J P.A two－dimensional quadrupole ion trap mass spectrometer［J］.J Am Soc Mass Spectrom，2002，13（6）:659－669.

［6］HAGER J W.A new linear ion trap mass spectrometer［J］.Rapid Commun Mass Spectrom，2002，16（6）:512－526.

［7］DOUGLAS D J，FRANK A J，MAO D.Linear ion traps in mass spectrometry［J］.Mass Spectrom Rev，2005，24（1）:1－29.

［8］CAMBELL J M，COLLINGS B A，DOULAS D J.A linear ion trap time－of－flight system with tandem mass spectrometry capabilities［J］.Rapid Commun Mass Spectrom，1998，12（20）:1463－1474.

［9］PARKS J H，SZOKE A.Simulation of collisional relaxation of trapped ion clouds in the presence of space charge effects［J］.J Chem Phys，1995，103（4）:1422－1439.

［10］GUAN S，MARSHALL A G.Equilibrium space charge distribution in a quadrupole ion trap［J］.J Am Soc Mass Spectrom，1994，5（2）:64－71.［11］SERWAY R A，JEWETT J W.Physics for scientists and engineers with modern physics，（8th edn.）［M］.Brooks／Cole，Belmont，CA，2010:693－695.

［12］FISCHER E.Die dreidimensionale stabilisierung von ladungsträgern in einem vierpolfeld［J］.Z Phys，1959，156（1）:1－26.

［13］TODD J F J，WALDREN R M，MATHER R E.The quadrupole ion store （Quistor）part IX.Space－charge and ion stability. A theoretical background and experimental results［J］.Int J Mass Spectrom Ion Phys，1980，34（3／4）:325－349.

［14］GUNA M，BIESENTHAL T A.Performance enhancements of mass selective axial ejection from a linear ion trap［J］.J Am Soc Mass Spectrom，2009，20（6）:1132－1140.

［15］SHAHA K，RAMACHANDRANB H.Space charge effects in rf traps:Ponderomotive concept and stroboscopic analysis［J］.Physics of Plasmas，2009，16（6）:062307.

［16］QIAO H，GAO C，MAO D，et al.Space－charge effects with mass－selective axial ejection from a linear quadrupole ion trap［J］.Rapid Commun Mass Spectrom，2011，25（23）:3509－3520.

［17］GORSHKOV M V，GOOD D M ，LYUTVINSKIY Y L，et al.Calibration function for the orbitrap FTMS accounting for the space charge effect［J］.J Am Soc Mass Spectrom，2010，21（11）:1846－1851.

［18］GUNA M，LONDRY FA.Tandem ion trap design with enhanced mass analysis capabilities for large populations of ions［J］.Anal Chem，2011，83（16）:6363－6367.

［19］MAGPARANGALAN D P，GARRETT T J，DREXLER D M，et al.Analysis of large peptides by MALDI using a linear quadrupole ion trap with mass range extension［J］.Anal Chem，2010，82（3）:930－9342.

［20］HERLERT A H，BORGMANN C B，KINK，et al.Effects of space charge on the mass purification in Penning traps［J］.Hyperfine Interact 2011，199（1／2／3）:211－220.

［21］XIONG X，FANG X，DENG Y，et al.Accelerated simulation study of space charge effects in quadrupole ion traps using GPU techniques［J］.J Am Soc Mass Spectrom，2012，23:1799－1807.

［22］MARCH R E，TODD J F.Practical aspects of ion trap mass spectrometry:Fundamentals of ion trap mass spectrometry［M］.CRC Press，2000.

［23］俞允强.电动力学简明教程［M］.北京:北京大学出版社，1999.