兴化站年最高水位序列趋势成分浅析
2013-05-29王品勇刘国钧
王品勇 刘国钧 樊 静
(江苏省水文水资源勘测局泰州分局 泰州 225300)
兴化站位于苏北里下河腹部区南官河上,在防汛防旱、工程调度中都有着不可或缺的重要地位。作为年际变化径流特征的主要水文变量的年最高水位序列,在频率计算中被当作纯随机变量,直接对未经处理的实测资料进行统计分析,分析结论缺乏合理性。为此,有必要对其中影响因素进行分析,使分析结论更趋合理。
1 序列成分分析
1.1PⅢ频率分析
对1952~2011年兴化站年最高水位和年降水量进行皮尔逊Ⅲ型频率计算。计算结果见表1。
根据表1,兴化站百年一遇的年最高水位x1%=3.44m,百年一遇的年降水量y1%=1753.4mm。1991年,年最高水位为3.35m,相应频率为1.5%,重现期67年;年降水量为2075.5mm,相应频率为0.0835%,重现期1198年。两相比较,前者不足百年,而后者已过千年,相差悬殊,频计成果明显缺乏说服力。
1.2序列因素分析
兴化站年降水量主要集中在主汛期6、7、8三个月(多年平均占比51.67%),由于该地区易旱易涝,该站年最高水位与年降水量有密切关系。采用1952~2011年60年的实测资料检验两者相关关系。取显著性水平α=0.01,由相关点据的个数n=60查“相关系数检验表”得临界线性相关数值r0.01=0.331,再列表计算年最高水位与年降水量这两变量的相关系数 r=Cov(x,y)/[σ(x)σ(y)]=0.764>r0.01=0.331,说明年最高水位与年降水量有较明显的线性关系。
前文1991年最高水位与降水量重现期的巨大差异,主要是由于所采用的资料未作分析处理。一般来说,当一个水文过程受确定性因素影响小且在时序变化上无相依性,那这一过程便属于纯随机过程。结合大量实测资料的佐证,年降水量序列就可以近似地作为纯随机序列;而年最高水位系列既受到年降水量及其年内分配影响,又受到下垫面及流域调节性能等确定性因素影响,为非随机序列。
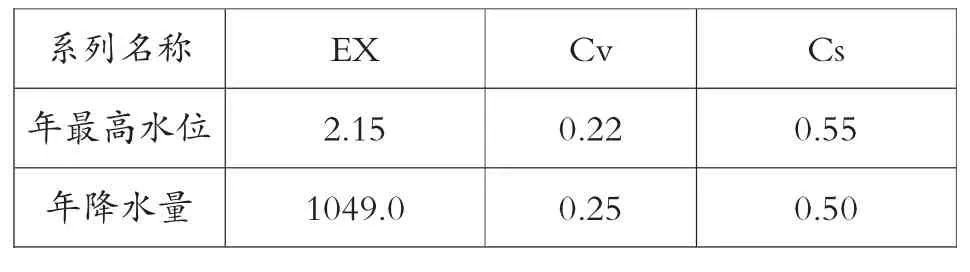
表11952~2011年兴化站年最高水位和年降水量皮尔逊Ⅲ型频率计算结果表
确定性因素表现形式一般包括周期性成分和突变、跳跃、趋势等暂态成分。兴化站年降水量和年最高水位序列不易受短周期影响,长周期对兴化站年最高水位的影响主要通过对年降水量的影响而产生,不另作影响因素考虑。突变是指流域内发生溃坝、决堤等突发性事件在水文序列中产生的水文变量突然有大幅度升高或降低的一种反应。本文所引用的资料始自1952年,不包含突变成分在内。跳跃一般出现于一次性大规模的拦河筑坝或大型水利枢纽工程建成前后,兴化站所在区域周边水利建设成就突出,存在跳跃成分。但为考虑问题的方便,将不算明显的跳跃成分因素归结为产生趋势成分因素的一部分。
趋势是一种有一定规则的变化,随着时间增长,对水文序列中的各值平均来说是增加或减少,这将造成序列长期向上或向下缓慢地变动,序列的任何参数都将随着时间增长呈现系统而连续的增或减的变化。兴化站年最高水位序列图(如图1所示)显示,该序列前段有明显的下降趋势,后段有上升趋势但不太明显。
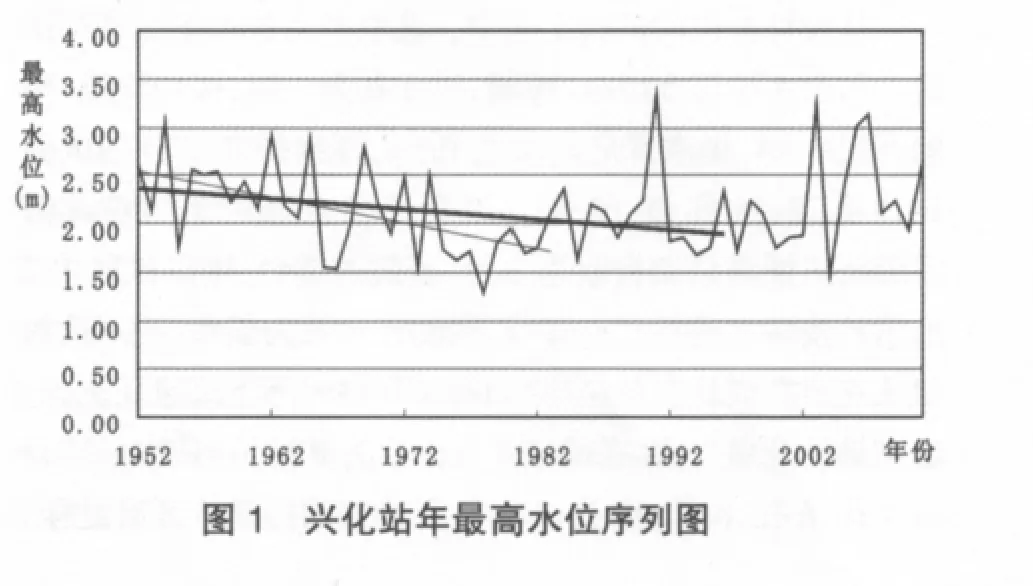
2 年最高水位的趋势分析
2.1趋势检验
采用坎德尔秩次相关检验法对兴化站年最高水位进行趋势检验。
检验所用统计量:U=τ/[Var(τ)]1/2
式中,τ=4p/[n(n-1)]-1,Var(τ)=2(2n+5)/[9n(n-1)]。
p为序列 x1,x2,…,xn所有对偶值(xi,xj,i
以上述序列图二次趋势线的最低点为界,分段对兴化站年最高水位序列作局部趋势检验。先初步假定该序列在1983年下降趋势结束,再利用检验手法来判断年最高水位序列中趋势成分是否明显。
对1952~1983年的最高水位序列作趋势检验。建立原假设H0为序列中无趋势成分,备择假设H1为序列中存在趋势成分。计算统计量U=-3.15;选择α=0.05,查正态分布临界点 Uα/2=1.96,因为│U│>Uα/2,所以拒绝原假设 H0,而接受备择假设H1,即序列包含有明显趋势成分。以同样步骤检验1983~2011年的最高水位序列,经计算│U│ 采用坎德尔秩次相关检验法对兴化站年降水量序列段作趋势检验。1952~1983年降水量序列段│U│>Uα/2,与同期年最高水位序列一致,局部趋势成分也明显;1952~1996年(共45年)年降水量序列│U│ 对1952~1996年最高水位序列段作趋势检验,经计算得│U│>Uα/2,此段序列存在趋势成分。综上,1952~2011年年最高水位序列存在局部(1952~1996年)趋势显著,这时显著的局部趋势已基本排除随机抽样造成的干扰。 新中国成立后,里下河地区实施了一系列以防汛抗旱为中心的水利建设,对削减洪峰水位特别是年最高水位作用明显。排涝能力随着排涝河的数目增加及其行洪标准加大、水利设施的配套完善而逐年加强,防洪效果逐渐增长,其对年最高水位序列的影响逐步形成。 假定趋势为线性趋势,用线性回归进行检验。线性模型用下式表示; εt为剩余项,是一数学期望为零的纯随机序列; a、b为系数。 按回归分析方法,计算兴化站1952~1983年最高水位序列段相应线性参数a、b的估计值以及的方差 线性模型中的参数a、b则可用上面的由回归方法求得的参数估值来代替。将代入线性模型得: 则均值为零的纯随机序列εt=xt+0.01062t-2.365; 当t=0,即未有趋势影响时,以ηt代表无趋势影响的序列,有: 据此式生成兴化站无趋势成分的年最高水位序列ηt。需要注意的是,虽从1997年开始,兴化站年最高水位序列不再呈现下降趋势,并不代表趋势影响因素的作用已经完结,而是说明从该年即t=45+1起,前期的趋势影响因素所造成的影响已趋于稳定,自此以后,代入模型中参与计算得t=45。 现在已从实测的年最高水位序列中排除了确定性因素的影响,又由于区域洪水特点,该序列在时序变化上也不存在相依性。因此,生成的无趋势成分的年最高水位序列ηt便也是一个近似的纯随机水文序列,可以直接用来进行频率计算。频率计算结果为:EX=2.45、Cv=0.20、Cs=0.50。 频率为1%的年最高水位η1%=3.77m,由所建线性趋势模型知: 如果百年一遇的水位在以后不论何时发生,因为序列局部趋势已停止,t=45,所以实际发生的水位应为3.29m。 针对1991年,最高水位是3.35m,对应t=40,无趋势影响时的水位ηt为3.77m。但如果这一水位在以后发生,那么不受趋势影响时的水位ηt为3.83m,在新配线上可查得其出现频率为0.815%,重现期为123年,结果更趋合理。 对兴化站年最高水位序列的频率计算采用该站年降水量序列作为参照,主要是为了探讨改进频率计算工作方法,实际做不到两序列的绝对同步。由排除趋势的模型所生成的年最高水位序列中1991年最高水位的重现期,远远赶不上同年降水量的重现期。导致两个线性相关的水文序列重现期相差巨大的原因,结合该地的历史与实际情况,笔者认为还有如下原因: 一是兴化地区汛期正常水位一般控制在1.30~1.50m,当水位低于1.50m,为满足灌溉及航运的需要,排涝系统基本上不发挥作用。二是所述趋势是指资料序列的整体平均情况,而事实上区域蓄排系统各年发挥的能力不平衡,有的是人为影响,有的由现时暴雨特点决定。 本文计算中忽略了面雨量的影响,对年降水量在面上分布的随机特性缺少考虑,而兴化站实际各种水位序列在很大程度上依赖于一定区域范围内平均降水量,年最高水位序列也不例外。本文计算中也忽略了除趋势以外的其他成分影响■2.2趋势成因分析
2.3无趋势影响的年最高水位序列

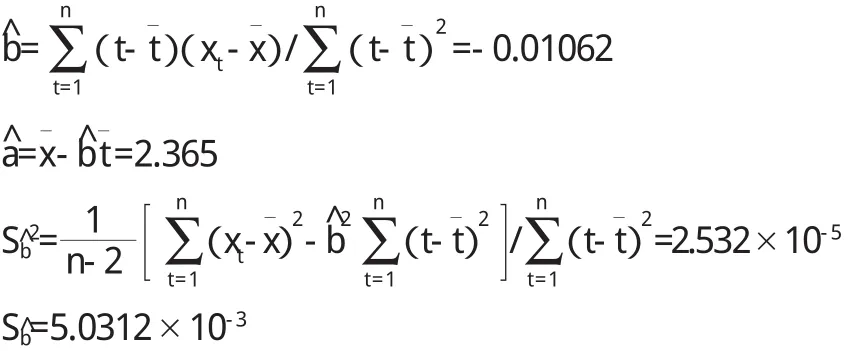
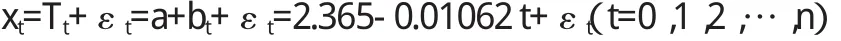

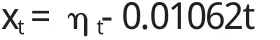
3结论
