DFIG风电系统最大风能捕获的滑模变结构控制方法

张细政，刘国荣

（1.湖南工程学院 计算机与通信学院，湘潭 411104；2.湖南工程学院 电气信息学院，湘潭 411101）

0 引 言

近些年来，风力发电技术得到迅速发展，其装机容量和市场份额不断增加.随着对风电系统研究和实施的不断深入，学者们逐渐认识到控制技术对于提高风电系统性能具有越来越重要的作用，因此，深入研究风电机组的建模和控制是非常有意义的［1］.在各种风力发电系统中，变速恒频双馈系统由于能量利用率高、功率因数可控及所需要的变频器容量小等优点成为很有竞争力的一种风力发电形式［2］.变速操作允许风电机组在最大空气动力效率下不断调整其发电机转速，电机侧的电力变流器可使高速轴转矩相应变化，因而使风力机可运行于不同的转速下，当风力机的叶尖速比达到最优值时，即可瞬时捕获最大的风能，有效提高发电机的使用效率.风电系统控制比较复杂，具有很大的难度，主要体现在如下方面：风力的随机性和风力机本质上的强非线性，DFIG电机控制的复杂性，系统参数通常有变化及电网电压波动等干扰影响［3］［4］.

风能的最大捕获是风电系统实现高效经济运行的重要保证，目前已有较为丰富的捕获算法.Hilloowala和Sharaf首先提出了最大功率点跟踪（MPPT）策略，基于极值搜索思想，采用“爬山”算法来使系统工作点接近于最优工作点［5］.基于MPPT，先后出现了一系列改进和变形的MPPT策略.其主要缺陷是需要获取较为完整的测量信息并对其进行高效处理，跟踪效果直接受限于搜索算法的性能.Bruey和Jatskevich等分别采用传统的PI控制方法完成了风电系统的发电机转速和功率PI控制［6］.Cutululis分别采用定量反馈理论（QFT）和增益调度理论（LQG）实现了永磁直驱风电系统的多模型鲁棒控制，可以灵活的适应不同风速下系统的多模型工作［7］［8］.基于反馈线性化方法，Matas和郭家虎分别设计了直驱同步风电机组和DFIG的滑模控制策略，对系统扰动和不确定性具有很强的鲁棒性，且实现较为简单［9］［10］.

滑模变结构是一类非常适合于处理系统不确定性的鲁棒控制技术，将其应用于风力发电系统时，主要优点是该方法只需要获取相对较少的状态／输出量信息，对参数的变化不敏感，且在选取合适大小的切换控制增益下，能较好的实现控制输入抖振和控制性能的平衡［11］［12］.

本文基于简化的DFIG状态模型，设计出了一种简单、实用的滑模控制策略，可实现定桨风力机最大风能的捕获，有效提高风能利用效率.首先建立起简化的双馈风力发电系统的数学模型，将能量优化从最优叶尖速比转化为对最优轴转速（发电机转速）的跟踪，然后利用滑模变结构方法设计滑模函数，推导出控制器结果.最后通过仿真对控制性能加以验证.

1 风力机－发电机模型

将风力发电系统从结构上划分为风力机传动和DFIG发电机两部分，分别建立起两个子系统数学模型.

1.1 风力机模型

在风速为vm／s下，定浆变速风力机捕获的风能和转矩可表示为：

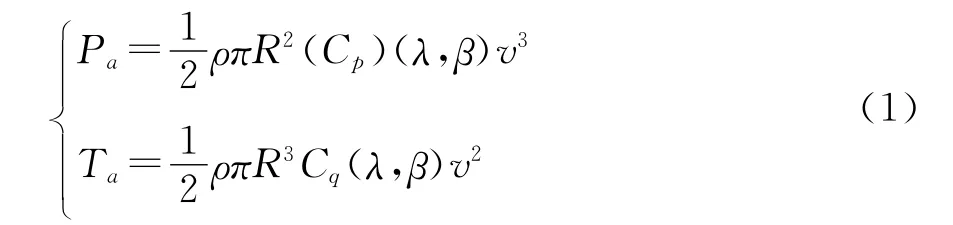
式中：ρ为空气密度，R为叶片半径，β为叶片节距角，λ为叶尖速比，且有λ＝ωtR／v，ωt为叶片转速，Cp（λ，β）、Cq（λ，β）是与β、λ有关的风能利用系数和转矩系数，Cp在特定点（λopt，βopt）处具有唯一最大值Cpopt.为保持叶尖速比取最优值βopt，对于给定的风速v，转速ωt应该和v保持同步增减，即需要调节发电机转矩以跟踪最佳叶片转速ωtopt＝λopt·v／R.

图1给出了风力发电系统的传动子系统结构，风力转矩Ta驱动叶片以ωt转动，经过增速箱后转速提升为ωg＝ngωt，其中ng为增速比.增速箱的低速端输入、高速端输出转矩分别为Tls、Ths.在克服发电机电磁转矩Tg作用后，Ths驱动电机以转速ωg运行于发电模式.

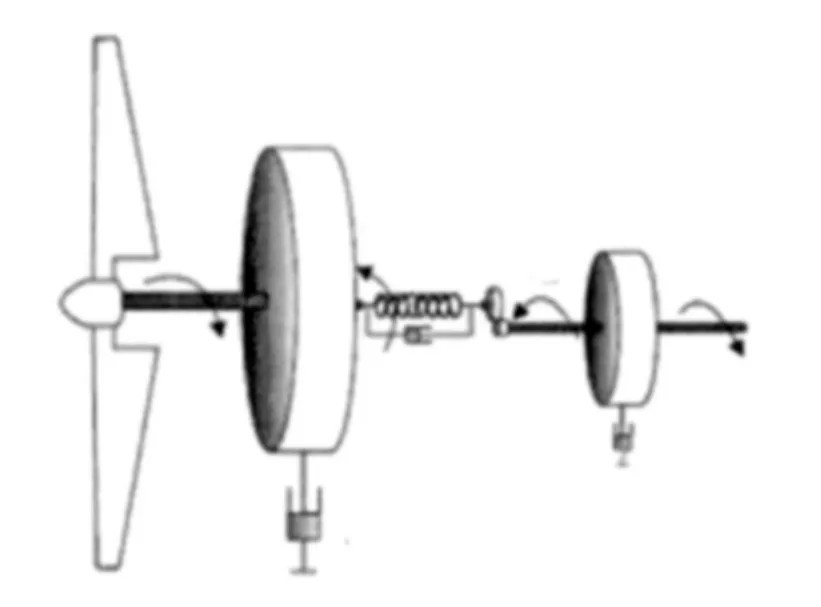
图1 风电系统传动环节结构

假设风力机低速转轴为理想刚性的，整个传动环节的运动方程可表示为

1.2 发电机模型

假定定浆、笼型DFIG是理想发电机，参数恒定，已知功率系数曲线，忽略叶片的动态性和发电机的响应时间，其降价状态方程为［4］：

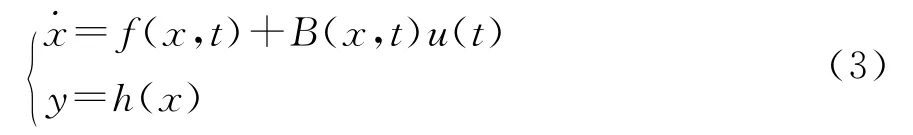
式中：状态变量x＝［x2x2］T＝［ωgTg］T，非线性函数为发电机电磁时间常数.由其数学模型，可知发电子系统的控制输入为Tg.

与其它采用定、转子电流或磁链为状态变量的全维模型不同，降价状态方程（3）只考虑发电子系统的机械特性，忽略其电气子系统特性，采用的状态变量是电磁转矩和转速.

本文中，为较好模拟实际的电磁转矩动态性，采用了如下一阶转矩响应模型

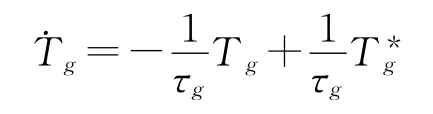
式中：参数电磁转矩u＝即为系统的控制输入，τg为发电机电磁时间常数.

2 发电机滑模变结构控制

2.1 滑模面设计

滑模设计的出发点是使得系统能尽可能的工作在最佳特性点（ωgopt，Tgopt）附近，实现能量的最大捕获.设计基于发电机转速和发电转矩二维平面上的滑模函数对其进行估计.

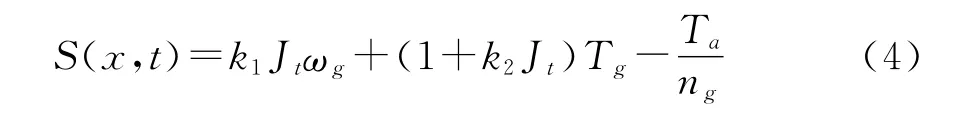
式中：Ks＝［k1，k2］T为系数矩阵，用于调整滑模运动的收敛速度.式（4）中，风力转矩Ta的实测比较困难，而发电机转速ωg是可测的，再结合高速端运动方程

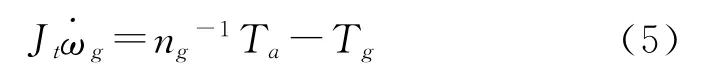
则式（4）可改写为

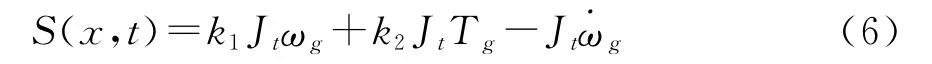
式（6）中状态变量的导数难以准确计算得到，实际中可运用二阶高通滤波器对其进行估计.

2.2 滑模控制器设计

一般来说，滑模控制器由等效控制ueq和切换控制usw两部分组成，即

按照滑模控制理论，一旦状态轨迹进入滑模面，系统运动即进入滑模运动，此时滑模函数满足

结合式（4）可得

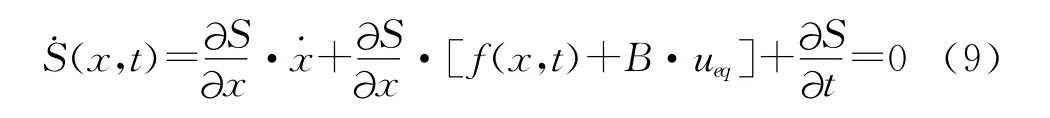
式中（8）、（9）可得滑模控制器的等效控制量

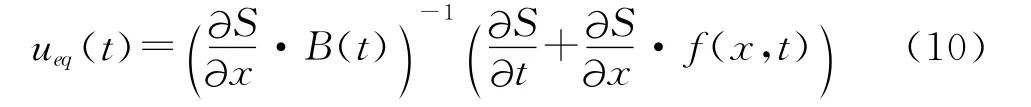
式中各编导数项计算如下

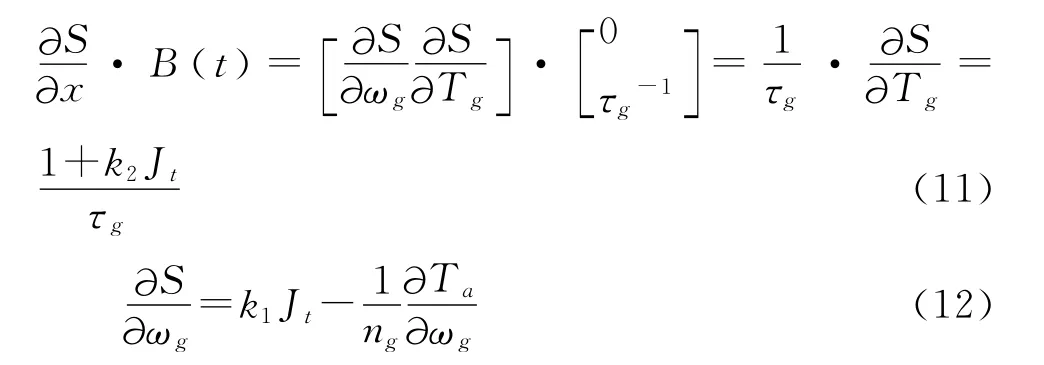
进一步的考虑刚性传动链，由式（1）结合最佳叶片转速式ωtopt＝λopt·v／R和转矩系数Cq（λ，β）＝Cp（λ，β）／λ，可计算出风力转矩对高速端发电机转速的偏微分

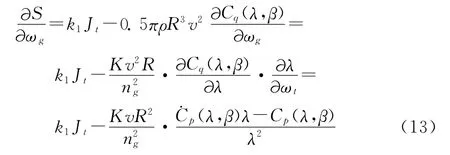
则由式（4）、（10）－（13），可得等效控制量为

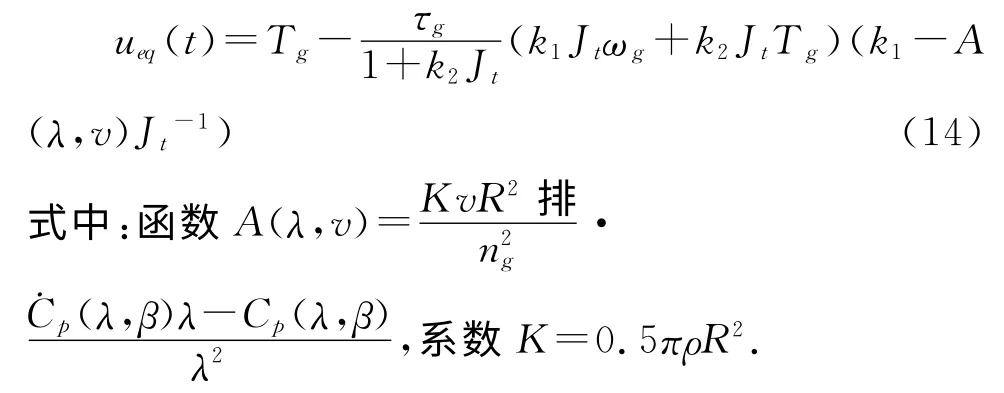
滑模控制切换量设计为

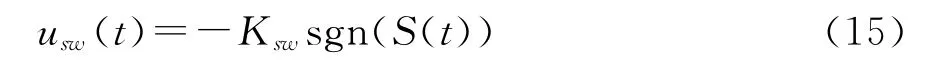
式中：ksw为切换增益，sgn（·）符号函数.实际中，为有效减轻输入控制量的抖振，可使用饱和函数取代式（15）中的符号函数，即

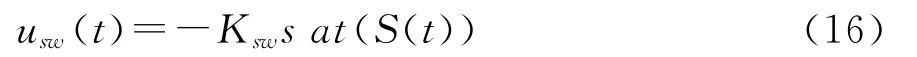
3 仿真与结果分析

对本文滑模控制策略进行了仿真研究，仿真用小型风力机特性参数与双馈发电机参数如下：

风力机参数－叶片半径R＝2.5m，转子总惯量Jtwt＝3×105kg·m2，最佳风能利用系数Cpopt＝0.47，最佳转矩系数λpopt＝7，摩擦系数Kt＝400 N·m·rad－1·s，齿轮箱增速比ng＝6.25，空气密度ρ＝1.25kg／m3.

DFIG发电机参数－额定功率6kW，额定电压220V，额定转速157rad－1·s，额定频率50Hz，2极，定子电阻1.265Ω，定子电感0.145mH，转子电阻1.43Ω，转子漏感0.145mH，互感0.139mH，转动惯量0.01kg·m2，电磁时间常数0.02s.

高通滤波器传输函数系数取为［0.01，0.2，1］，滑模系数k1＝－2，k2＝－5，ksw＝0.5.

依据文献［3］方法，图2给出了仿真时生成的风速曲线，平均风速为7.5m／s.图3为本文控制方法下的发电机转速ωg，可见实际转速能很好的跟踪最优转速ωtopt.在本文滑模控制作用下，图4为实际风能利用系数，可见在经过短暂的调整后，能快速达到最佳风能利用值0.47.图5为叶尖速比变化曲线，图6为滑模函数变化曲线.

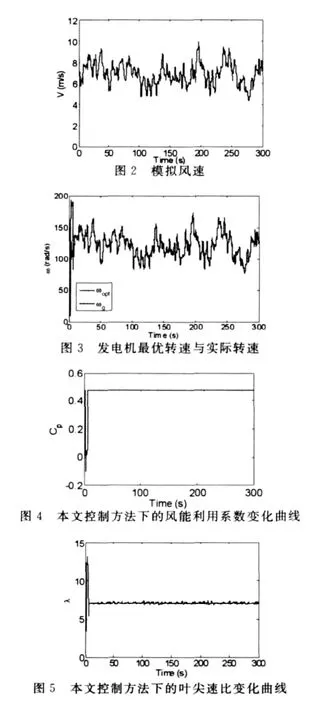
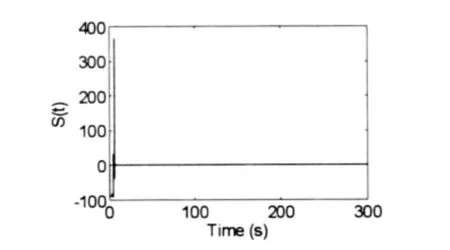
图6 滑模切换面

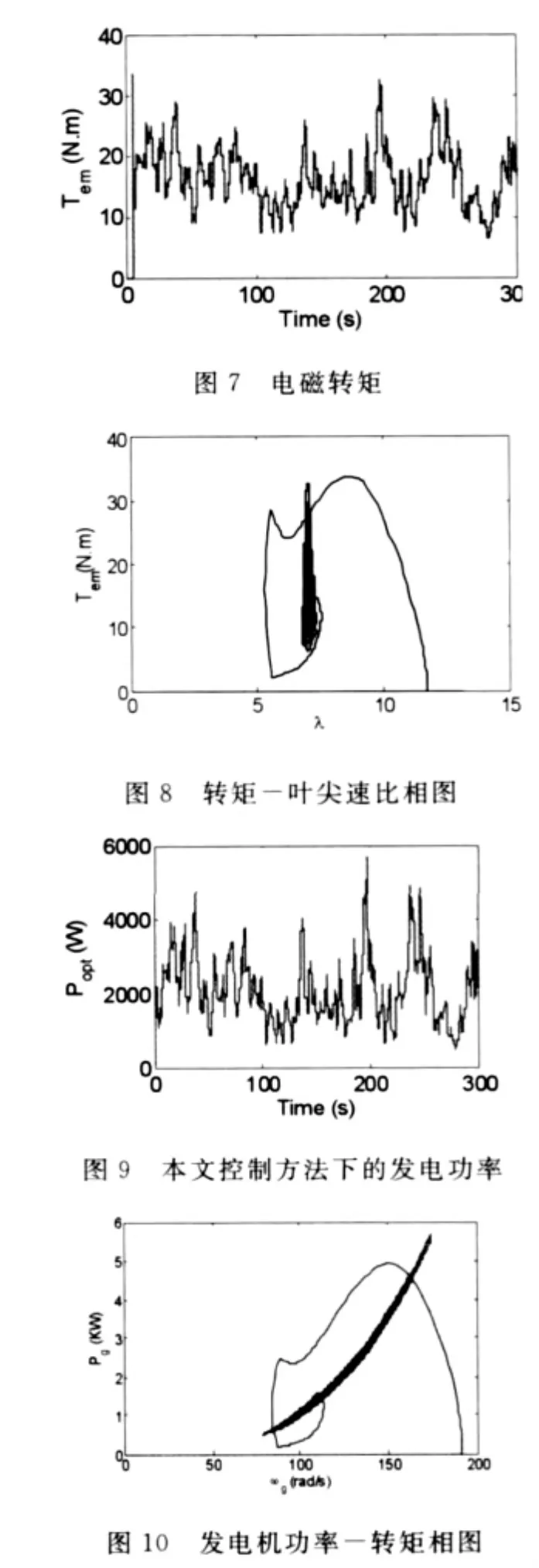
图7、图8分别为发电机电磁转矩及其与叶尖速比的二维相图.图9为本文滑模控制方向下的发电功率，能较好的追踪风速变化情况，实现最大风能捕获.图10为发电功率与发电转矩的二维相图.

4 结 论

提出一种DFIG风电系统的新型鲁棒滑模控制方法，利用滑模DFIG控制器对发电机转速和转矩进行控制，实现对风力机最优转速的鲁棒跟踪，稳定在系统的最佳工作点上，进而获得在额定发电功率内的最大风能追踪.仿真结果表明，本文所设计方法控制性能良好，验证了所提模型的正确性和控制策略的有效性.

［1］刘万琨，张志英，李银凤，等.风能与风力发电技术［M］.北京：化学工业出版社，2006.

［2］Joselin Herberta G M，Iniyanb S，Sreevalsanc E，et al.A Review of Wind Energy Technologies［J］.Renewable and Sustainable Energy Reviews，2007，11（6）：1117－1145.

［3］Koutroulis E，Kalaitzakis K.Design of a Maximum power Tracking System for Wind Energy Conversion Applications［J］.IEEE Trans.on Industry Electronics，2006，53（2）：486－494.

［4］黄守道，王 毅，王耀南.无刷双馈电机风力发电控制系统与仿真研究［J］.湖南大学学报，2004，31（1）：37－40.

［5］Hilloowala R.M.，Sharaf A.M.A Utility Interactive wind Energy Conversion Scheme with an Asynchronous DC Link Using a Supplementary Control loop［J］.IEEE Transactions on Energy Conversion，1994，9（3）：558－563.

［6］Bruey，S.，Jatskevich，J.，Dumont，G..A PI Control of DFIG－Based Wind Farm for Voltage Regulation at Remote Location［C］.IEEE Power Engineering Society General Meeting，2007：24－28.

［7］Cutululis N.A.，CEANGA E.Robust Control of an Autonomous Wind Power System［J］.Journal of Control Engineering and Applied Informatics，2004，6（4）：3－12.

［8］Munteanu I.，Cutululis N.A.，Bratcu，A.I.Optimization of Variable Speed Wind Power Systems Based on a LQG Approach［J］.Control Engineering Practice，2005，13（7）：903－912.

［9］郭家虎，张鲁华，蔡 旭.双馈风力发电机的精确线性化解耦控制［J］.电机与控制学报，2009，13（1）：57－62.

［10］Matas，J.，Castilla，M.，Guerrero，J.M.Feedback Linearization Of Direct－Drive Synchronous Wind Turbines Via a Sliding Mode Approach［J］.IEEE Transactions on Power Electronics，2008：1093－1103.

［11］Brice B，Tarek A A，Mohamed E H，et al.Sliding Mode power Control of Variable－speed Wind Energy Conversion Systems［J］.IEEE Trans.on Energy Conversion，2008，23（2）：551－558.

［12］Hernan D B，Ricardo J M.Dynamical Variable Structure Controller for Power Regulation of Wind Energy Conversion System［J］.IEEE Trans.on Energy Conversion，2004，19（4）：756－763.