列联表检验在疾病成因中的应用

赵鹏辉，崔 蕊

(大庆师范学院 数学科学学院，黑龙江 大庆163712)

0 引言

列联表是统计同时确定两个变量的值，对总体中要讨论的个体分类并分组，将其分布进行分析，来探究分类变量间的相关性［1］。对疾病和疾病成因进行分级，建立列联表的基础上，对疾病的成因进行分析，便于对疾病的预防与治疗，这样列联表在医学中的应用极为广泛。

1 列联表检验和卡方检验

1.1 列联表检验

统计学中，对研究对象进行分类并对样本的频数进行统计并进行探究。依据样本分组的指标变量，对其排序即得到列联表。分析研究列联表中的数据，来检验两个变量的关系，应用假设检验中的卡方检验研究列联表中分类变量是否独立，称这种检验为列联表检验［2］。列联表分析法的应用极为广泛，它可以分析研究总体中个体的属性之间是否相关，称为独立性检验。例如，帕金森与其性别是否有关?在以二者为研究对象所列出的列联表中，以Pi.、Pj.和Pij代表研究对象中样本分类于等级Ai，等级Bj，以及同时属于AiBj的概率，帕金森与性别之间是否相关这样的问题可以转化为在统计学中的问题，表述为H0:Pij= Pi·Pj，进行列联表检验，查对临界值表若χ2值足够大，则拒绝假设，即二者相关。依此方法检验即可以较大的把握判定出性别与帕金森是相关的。明确变量之间的相关性后，还需要引入某个定量指标例如列联系数来刻画二者的相互联系的程度［3］。

1.2 卡方检验

假设检验方法中的卡方检验的应用较为广泛，它包括利用卡方检验对两个率或两个构成进行比较。卡方检验能对多个率或多个构成比进行比较以及对分类变量的性质进行相关分析。卡方检验用来判断构成比之间是否存在差别并推断分类变量之间是否有关系［4］。

对总体分布中的样本的频数分布或是列联表中的频数进行检验，卡方检验的应用性较为广泛，用假设检验分析并探究它是服从某种理论分布还是某种假设分布。即在推断总体的分布时参照样本的分布，这种检验方法属于自由分布中的非参数检验。它主要应用于一个样本分为多种类，或多个样本各有多种类的数据，即比较两个或两个以上的构成比的统计方法，在药学与医学中应用极为广泛，在应用统计中常常需要用到卡方检验进行假设检验［2］。

卡方检验是对样本的实际频数与期望频数进行比较并比较二者之间的偏离程度，它们相差或偏离的幅度大小与卡方值的大小相关性很大，当二者完全相符时卡方值为0，而卡方值越小则表明二者越趋于相符，卡方值越大，则代表二者不相符［5］。

1.3 列联表的卡方检验［5］

若列联表四个格子排序后的实际值分别为a，b，c，d，n = a+b+c+d，则对列联表进行卡方检验，为此引进统计量

这个统计量服从 (p -1)(q -1)的卡方分布，其中p 代表行数，q 代表列数.这里要求样本含量大于40，而且列联表中的理论频数不小于5，或者小于5 的数据不超过数据的五分之一，当样本量较小时，可直接求得概率值进行判断，当样本量大于40，而频数小于5 时，通过对卡方值的进一步修正即可判断［2］。

2 列联表检验在疾病成因中的具体应用

2.1 糖尿病与酗酒的相关性分析

某医疗机构为了了解糖尿病与酗酒是否有关，进行了一次抽样调查，共调查了200 个成年人，其中酗酒者106 人，不酗酒者94 人，调查结果是:酗酒的106 人中有82 人患糖尿病，24 人不患糖尿病;不酗酒的94 人中44 人患糖尿病，50 人不患糖尿病，研究对象可以分为I 和II，1 有两类取值，即酗酒与不酗酒，II 有两类取值，即患糖尿病与不患糖尿病，统计以上数据可得到如下列联表:

表1 糖尿病与酗酒人数统计表

我们要研究的问题是能否依据这些数据来判断患糖尿病与酗酒相关，很多实际问题需要判断分类变量之间是否有关系，既二者是否相互独立，根据列联表和卡方检验的性质，我们可以利用它们来探究疾病的成因。可以根据以根据抽样调查出来的数据绘制直方图1、图2。

图1 糖尿病与酗酒人数直方图1

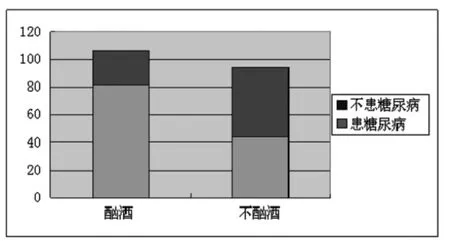
图2 糖尿病与酗酒人数直方图2

从图中分析，在直观印象认为患糖尿病与酗酒是有关的，而实际是否相关，需要用统计观点来考察这个问题，利用列联表来探究以下问题:

1)判断酗酒与否和患病的可能性大小的差异性及其标准;

2)差异性达到多大才能作出患糖尿病与酗酒有关的判断;

3)能否用数量来刻画二者相关的判断;

4)做出相应判断的把握为多大。

通过样本数据的计算得出，在不酗酒者中患糖尿病所占人数比重为46.81%;在酗酒者中患糖尿病所占人数的比重为77.36%。

上面我们通过分析数据和图形，得到的直观印象是酗酒和患糖尿病有关，还需要利用统计观点做出判断。利用列联表以及假设检验来分析研究这个分类变量的相关性的问题。现在想要知道能够以多大的把握认为酗酒与糖尿病有关，由抽样的随机性，根据样本得到的推断可能正确也可能错误。利用χ2做假设检验，对所推断的变量之间进行估计，为使估计较准确，应使样本量n 尽量大一些［6］。

为此先假设:H0:酗酒与患糖尿病不具有相关性

H1:酗酒与患糖尿病具有相关性

用M 表示酗酒，N 表示患糖尿病，则命题酗酒与患糖尿病没有关系等价于“酗酒与患糖尿病独立。即假设H0等价于P(MN)= P(M)P(N)。在H0成立的条件下，构造出与H0矛盾的小概率事件，如果样本使得这个小概率事件发生，就能以一定把握说明H1成立;否则H0成立。

为了一般化，将上表中的调查数字用字母代替，则得到2 ×2 列联表

表2 糖尿病与酗酒人数列联表

在表2中，事件MN 发生的频数为a;事件M 和N 发生的频数分别为a +b 和a +c。由于在大事件中频率接近于概率，所以在H0成立的条件下应该有酗酒者中患糖尿病的比例等于不酗酒者中患糖尿病的比例，即

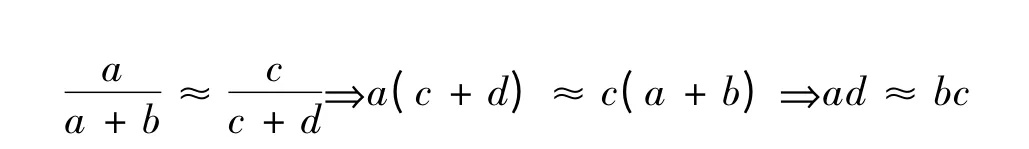
| ad - bc |其值越小，则说明酗酒与患病之间的关系越弱;其值越大，则说明酗酒与患病的关系越强。通过计算有:

统计学中常常用卡方统计量来描述实际观测值与估计值的差异，为此构造卡方统计量χ2= ∑来使不同样本容量的数据有统一的评判标准，构造一个统计量称它为卡方统计量

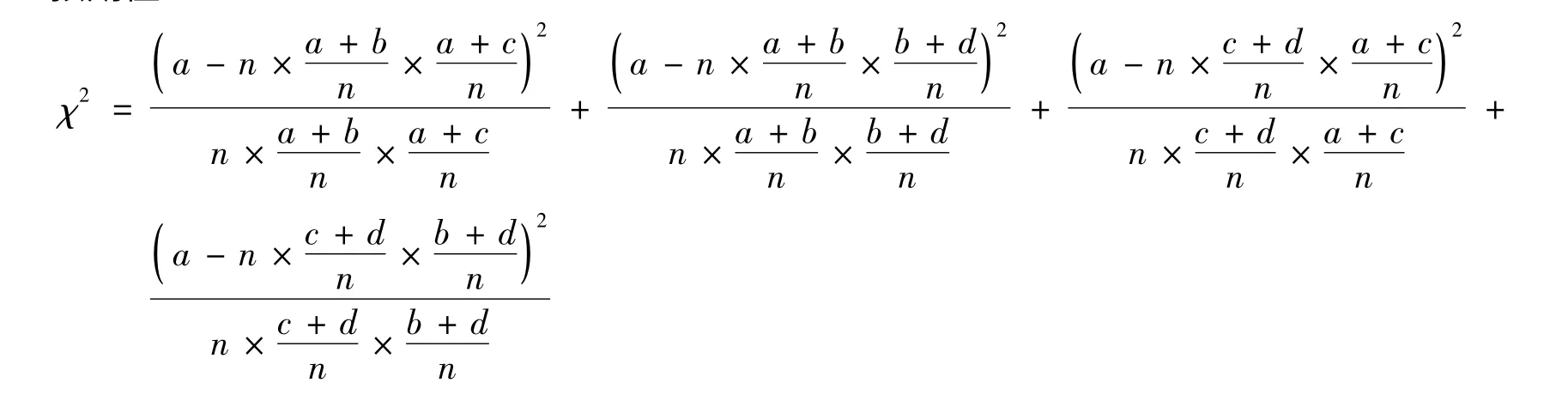
因此若H0成立，即酗酒与患糖尿病没有关系，则χ2的观测值应该很小。最后查对临界值表来作相应判断。

表3 χ2 检验临界值表

参照上表即可以一定的把握进行判断，其意义如下表所示:

表4 χ2 检验临界值表的意义

因此可以依据这些步骤来验证酗酒是否与患糖尿病有关，通过计算可知

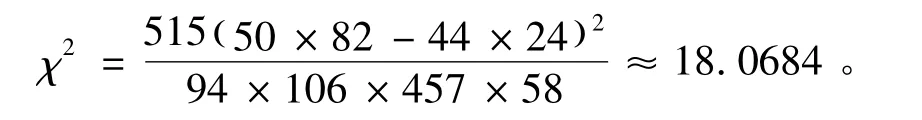
在H0建立的情况下χ2大于10.828，出现这样观测值的概率不超过0.001，因此99.9%的把握认为H0不成立，即99.9%的把握认为患病与酗酒有关。

2.2 疾病与疾病之间的相关性分析

2.2.1 简介交叉列联表及SPSS［4］

在实际问题分析中，除了需要对某个单个变量的分布情况进行分析外，还要分析多个变量在不同取值情况下的数据分布情况，而更加深刻的分析变量之间的相关性，即为交叉列联表分析。当有多个因素影响所调查的对象时，通过交叉列联表可以确定这些因素与所研究的样本之间的相关性且能分析出这些因素之间的关系。多个特征决定的分类变量的频数的排序分布所成的表定义为列联表，又定义它为频数交叉表，在SPSS 的Crosstabs 过程可以得到交叉列联表，它可以提供了多种检验方法和相关性度量方法，其中在分析列联表资料的数据中常常结合到假设检验中的χ2检验。所以在分析研究分类变量的性质时可以通过调查的样本数据来得到二维交叉列联表，然后通过得到交叉列联表对这两个变量的关联性进行分析。在这过程中，借助假设检验中的非参数检验和能准确刻画变量间相关程度的统计量。在本例中，利用SPSS 所提供的相关系数适用于不同类型数据，相关性检验的原假设H0:行列变量之间相互独立，显著关系不明显，每个单元格的频数期望值和实际频数相差不大，不拒绝原假设;如果二者相差很大，则拒绝原假设，并根据SPSS 检验，来判断是否存在相关关系［6］。

同列联表所介绍的一样，交叉列联表中各表格的期望值大小应大于1，小于的个数不能超过的表格，这种情况应对假设检验的统计量即卡方量进行修正。

在SPSS 中，检验相关关系中的方法中一下三种方法较为常用:

1)卡方检验:对行列变量之间是否相关进行验证。χ2=，其中f0表示实际观察频数，f1表示期望频数且统计量服从自由度为 (行数-1)(列数-1)的卡方统计。若在SPSS 中判断行列变量之间的相关性需要计算卡方统计量时和相应的相伴概率，常适用于名义变量的计算。

2)ψ 系数:计算公式是由χ2修改得到的，计算变量的相关系数。其中0 ＜ψ ＜1 ，M = min (行数，列数)。

3，列联系数:计算公式由χ2修改得到的，计算相关系数，但是它常常应用于分类变量的计算，其值为C

2.2.2 事例探究

在生活中，人们会患有多种疾病，我们常常关心这些疾病之间是否相关，一些高血压患者常常患有心脏病，那么血压疾病和心脏病是相互影响的还是独立，这可以利用交叉列联表来分析血压与心脏病之间的关系。

在抽样调查的过程中，将调查对象相对于血压以及心脏按健康的程度进行分级，即健康、亚健康、患病三类，形成血压等级和心脏健康等级的交叉列联表，并考察血压和心脏间有无关联性。

以某患病人群为样本进行抽样调查，利用SPSS 对所得到的数据进行操作。

表5 患病人群的血压及心脏健康程度分级统计表

依据前文对列联表以及假设检验的介绍，可以依此分析步骤探究问题:

1)提出原假设H0:血压与心脏的健康状况这两个变量互相无影响;

H1:血压与心脏的健康状况不相互独立。

2)之所以利用交叉列联表分析是由于这两个变量不是连续型而都属于离散分类型。

3)采用SPSS 操作，利用Chi - Square 卡方检验、皮尔森卡方检验(Pearson)、似然比卡方检验(Likelihood - ration)、连续性校正卡方检验来探究心脏的健康与否与血压的关系。通过样本的数据可以由SPSS 输出以下主要内容:

表6 患病人群的血压及心脏健康程度分级计数与期望对比表

表7 Chi - Square 卡方检验

在上表中看出χ2统计量的值为225.274，所对应的p 值为0.000 .由于p 值远远小于通常使用的显著性水平，因此检验的结论是拒绝原假设，很大把握认为血压的健康状况和心脏的健康状况是相互独关的。

3 列联表的相关分析

列联表将研究对象按某些特征分类并统计排序列出的数据表。由于样本所涉及的数据形式较简单，在统计检验中常常出现错误，常常会因选择统计方法的不适宜;或者数据不满足统计方法的条件而出现错误［7］，列联表的具体特征决定列联表检验的统计方法，列联表常常又可以分为相关列联表和独立列联表。前者的两个变量的特性完全相同。因此首先需要检验这个表中的两个变量特性是否形同。如果其中的两个变量的特性不同，则它是独立列联表。在与假设检验结合的过程中假设检验的结论，仅仅代表样本从同一总体中抽取的概率。例如当药效的差异性并不明显时，并不代表两种药的药效相同，只能说这两种药作为样本来自同一总体的概率大。而当两种药的治疗率差异性较大时，这并不能说明其中一种药的药性明显高于另一种药的药性，只能代表两种药从同一总体抽取的可能性或概率小，也存在着这两种样本来自不同的总体的可能性，此种差异具有代表性。因此，作出有无差异性或相关性的结论，要从实际并结合专业上加以研究，要根据医学上的实际意义来评论。同时注意在假设检验抽取样本数据时最好采取抽样调查并具有随机性，且分类变量除在控制处理条件不同外，应尽量使其他条件相同，这样才能避免其它条件的干扰。不能以百分百的把握对检验结果下结论，这是由于显著性性水平不是固定的而是是人为规定的，相对的。以根据P ＜0.01 作出的结论，即使有99% 的把握来说明其关系，仍有1% 错误的可能。

在对样本进行定量的分析时，假设总体服从正态分布，并采取参数检验统计方法分析研究。而对于总体分布未知的情况下和对定性资料的分析，无法进行参数检验，常采用非参数检验方法。例如χ2检验，列联表分析是非参数检验方法中应用最广泛的方法之一，它在经济、社会、医学、教育等学领域定性分析中应用的较为广泛，它是定性资料进行定量分析的基础，在医学的应用中极为广泛，适合医学中难以量化的定性变量间相关或独立性分列。列联表独立性检验方法最大的优点就是让我们从孤立的数据本身分析问题的本质，及时的发现问题和解决问题［8］。

［1］陈希孺.数理统计理论［M］.北京:科学出版社，1981:203 -209，297 -299.

［2］杨廷芬.2 ×2 列联表检验方法的回顾与比较［D］.广州:中山大学硕士学位论文，2009:9 -12.

［3］孙振球，徐勇勇.医学统计学［M］.北京:人民卫生出版社，2008:136 -156.

［4］方颖.利用SPSS 软件处理临床治疗率［J］.医学理论与实践，2011，24(16):15 -17.

［5］何平平.配对设计2 ×2 列联表的精确检验方法及应用［J］.中国卫生统计，2006(5):10 -12.

［6］B.S.Everitt.The Analysis of Contingency Tables［M］.London，1977:11 -36.

［7］陆运清.列联表资料检验的几种常见错误辨析［J］.统计与决策，2010(15):161 -163.

［8］蒋庆琅.实用统计分析方法［M］.方积乾，等译.北京:北京医科大学，中国协和医科大学联合出版社，1988:102，118 -134.