利用相似产品信息的冷贮备系统可靠性评估

李新翼，郑海鹰

(温州大学数学与信息科学学院，浙江温州 325035)

利用相似产品信息的冷贮备系统可靠性评估

李新翼，郑海鹰†

(温州大学数学与信息科学学院，浙江温州 325035)

以泊松型部件冷贮备系统为背景，主要讨论了在有继承因子情形下的冷贮备系统的可靠性评估问题．通过引入继承因子，进而得到混合先验分布，然后运用Bayes方法对冷贮备系统的可靠性指标进行估计．最后通过仿真算例对所给方法的有效性进行了验证．

冷贮备系统；可靠性；Bayes估计；继承因子

冷贮备系统是可靠性工程中的一类典型系统，能够反映某些工程结构的可靠性逻辑关系．所谓冷贮备是指贮备的部件不失效也不劣化，贮备期的长短对以后使用时的工作寿命没有影响．目前，关于冷贮备系统可靠性的研究很多，如文[1-2]对部件寿命服从指数型的冷贮备系统的可靠性进行了讨论，但对由泊松型部件及成败型开关组成的冷贮备系统的可靠性评估尚未涉及．在实际工程中，产品和老产品（或相似产品）属于不同的型号或批次，它们之间存在不同程度的相似性，又有一定变异性，因此它们本质上不属于同一总体，使用传统的Bayes评估将导致评估结果和实际有较大差距．针对这一问题，基于信息论的角度考虑，我们应该充分利用产品各方面的有效信息才能更为有效地评估产品的可靠性．本文所给方法引入了继承因子，用信息融合的原理将这两类信息融合成一个混合先验，采用Bayes方法描述了产品的继承性，使得评估结果更具稳健性和有效性，最后通过仿真实例与传统的Bayes方法进行了比较，证明了所给方法的合理性和有效性．

1 系统的可靠性

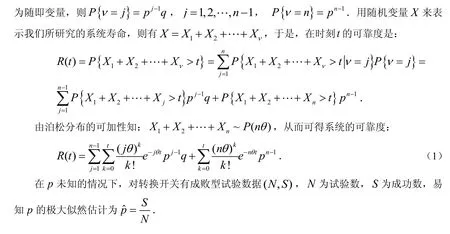
2 部件参数的传统Bayes估计

2.1 Bayes估计

2.2 多层Bayes估计

3 部件参数基于混合先验分布的Bayes估计

3.1 混合先验的确定

先验分布应该既体现这种继承性又要体现由于改进而带来的不确定性．文献[3]认为可以采用均匀分布来描述新产品可靠性的不确定性，此时取混合Ga(α, λ)分布为先验分布，即

其中0≤ρ≤1，ρ称为继承因子，反映新产品和老产品在可靠性方面的相似程度，1-ρ称为更新因子，ρ越大说明新产品在老产品基础上改动越小，当ρ=1时，认为两总体是完全相同的，此时混合先验π(θ)就是共轭先验π (θ)，也就是完全使用历史样本作为先验信息；而ρ越小则说明新产品在老产品的基础上改动越大，当ρ=0时，认为两总体完全不同，此时混合先验πθ)就是[0,1]上的均匀分布，也就是完全不用历史样本，在无先验信息的情况下，基于Bayes假设确定先验分布；当0＜ρ＜1时，是介于两者之间的情形，即两总体是相似（或者说是相近）的，所以，混合先验π(θ)的使用是对经典统计方法和传统Bayes方法的合理折衷，其综合考虑了各种情况，可以适用于更加广泛的范围，比共轭先验π (θ)更加合理．

如果有多种相关产品的可靠性信息可利用，则构造如下的混合Ga(α, λ)分布为先验分布：

3.2 继承因子的确定

混合先验带来了一个新的参数继承因子ρ，它是产生历史样本与现场样本的两总体的相似程度的度量，对可靠性评定的结果有着非常大的影响．文献[3]指出可以由专家根据产品的相似程度给出ρ的值，但这种依靠专家经验的方法很难做到准确．在文献[4]中，利用两样本的卡方拟合优度检验，给出了确定继承因子ρ的方法．

3.3 基于混合先验的Bayes估计

4 算例分析

表1 航材的需求量

表2 火箭弹射座椅系统各子系统的试验结果

3）比较分析：由传统Bayes方法得到的参数估计值与由基于继承因子的混合先验而得到的参数估计值的结果比较接近，从而说明了本文方法的合理性．两种方法的区别在于继承因子的引入，传统Bayes方法仅仅采用现有的试验数据进行评估，而基于融合先验的评估不仅有效利用了历史样本信息，而且充分考虑了产品之间的相似性、继承性，比单纯使用试验数据更合理．此外，该方法的计算也比传统Bayes方法的简单．通过以上分析可知，利用相似产品信息的系统可靠度比用传统Bayes方法得到的系统可靠性更加合理，更符合实际．

5 结束语

本文通过利用相似产品信息，采用混合先验分布，在引入继承因子的情况下对系统的可靠性进行评估．传统的Bayes方法只考虑产品的继承性，而忽略了新产品由于研制改进而带来的不确定性，这种混合先验分布综合地考虑了产品在设计和改进中的信息产品之间的相似性、继承性，因此更符合工程实际．此外，本文对只有一种相似产品信息的情形进行了讨论，但在实际工程中可能存在有多种相似产品信息的情况，这就需要对继承因子的确定方法和相似产品信息间的相关关系进行进一步的研究以满足工程实际的需求．

[1] 曹晋华, 程侃. 可靠性数学引论[M]. 2版. 北京: 高等教育出版社, 2006: 45-52.

[2] 晋佑顺, 谭伟. 开关寿命指数型冷贮备系统的可靠性评估[J]. 科学技术与工程, 2010, 32(10): 7871-7874.

[3] Kleyner A, Bhagath S, Gasparini M, et al. Bayesian techniques to reduce the sample size in automotive electronics attribute testing [J]. Microelectronics Reliability, 1997, 37(6): 879-883.

[4] 王玮, 周海云, 尹国举. 使用混合Beta分布的Bayes方法[J]. 系统工程理论与实践, 2005, 25(9): 142-144.

[5] 赵洪军, 齐校锋, 刘海翔. 基于泊松分布的航材库存决策优化研究[J]. 长沙航空职业技术学院学报, 2009, 9(1): 40-43.

[6] 董海平, 蔡瑞娇, 王玮. 基于混合Beta分布的火箭弹射座椅可靠性评估[J]. 航空学报, 2009, 30(2): 232-235.

[7] 李亿民. 关于指数分布无失效数据的一种Bayes分析[J]. 山东理工大学学报, 2006, 20(2): 17-19.

Assessment of Reliability for Cold Standby System Using Test Information of Similar Products

LI Xinyi, ZHENG Haiying
（School of Mathematics and Information Science, Wenzhou University, Wenzhou, China 325035）

Under the background of poisson-shaped cold standby system, the paper focuses on the reliability assessment of cold standby system in the case of inheritance factor. By introducing inheritance factor, the mixed prior distribution was obtained, and then the reliability index of the cold standby system was estimated by using Bayes method. Lastly the effectiveness of this method was tested with simulation.

Cold Standby System; Reliability; Bayes Estimation; Inheritance Factor

O213

A

1674-3563(2013)03-0017-07

10.3875/j.issn.1674-3563.2013.03.004 本文的PDF文件可以从xuebao.wzu.edu.cn获得

(编辑：王一芳)

2012-11-21

李新翼(1987- )，男，安徽合肥人，硕士研究生，研究方向：应用统计．† 通讯作者，wzzhying@163.com