基于模糊失效阀值的性能退化数据可靠性分析

杨 恒，徐格宁，韩子渊

（太原科技大学 机械工程学院，山西 太原 030024）

可靠性是研究产品是否能够顺利完成某个规定功能的概率的学科，是产品质量的一个度量准则.随着社会经济的发展，对产品（如核电用起重机）的可靠性的要求越来越高.产品的寿命是产品可靠性的直接体现，怎样通过产品的寿命数据对产品的可靠性进行分析是可靠性研究迫切需要解决的问题.在产品的生命周期中，性能退化是产品的一个显著特征，鉴于此，国内外学者开展积极的研究，文献［1—2］提出了利用实时获取的性能退化数据对产品进行可靠性评估；文献［3—4］提出了利用Parzen核密度估计构造滑动神经网络和以贝叶斯方法的实时估计性能退化数据可靠性分析方法.文献［5—10］分别提出了Poisson－Normal过程、模糊C－均值（C为预定的类别数目）、小脑模型神经网络、自组织特征图神经网络、逻辑回归、隐马尔可夫模型、Gamma过程等方法解决产品性能退化情况下的可靠性评估，其共同处都是针对一个确定失效阀值的情况进行研究.然而在实际中，产品的失效阀值往往随着环境、载荷、条件的变化而变化，表现出不确定的性质，文献［11］将失效阀值作为一个随机变量，利用相对失效的概念解决了失效阀值为随机情况下的问题，文献［12］把失效阀值为随机变量的情况应用到了柱塞泵性能退化的可靠性分析上.

本文根据产品的失效阀值在实际中表现出亦此亦彼的模糊性特点，在确定失效阀值的基础上，引入模糊理论方法，将失效阀值看成是模糊区间，利用模糊区间和相关的隶属函数代替固定值对产品的可靠性进行评价，使得理论计算与实际情况更接近.

1 在确定阀值下的性能退化数据的产品的可靠性分析

假设某次退化试验中共有m个样品进行规则型性能退化试验，在n个给定的时间点t1＜t2＜…＜tn，分别采用相同的方法进行测量，获得如下退化数据：

数据中xitj为第i（i＝1，2，…，m）个样品在第tj（j＝1，2，3，…，n）时间点的测量的参数退化值，设产品i在第tj时间点测量的性能参数为yi（tj），它随使用时间的增加逐渐单调下降，产品i初始性能值记为yi0，设xitj＝yi0－yi（tj），表示到tj时刻产品i累积退化量的大小.由于产品i的退化量单调上升，对于任意的ti，tj，如果ti＞tj，必有xiti＞xitj（单调增加）.

假设产品在测量点tj的退化量分布符合正态分布，利用正态分布的随机过程来描述退化量随时间变化的情况.假设｛xitj，tj＞0｝为一个随机正态分布，因此，它具有如下特性：

（1）对于产品i，tj＝0时，xitj＝0.

（2）对任意的时刻tj，xitj～N（μtj，σtj）为正态分布函数，μtj，σtj分别为tj时刻的退化均值和方差.

（3）xitj是独立增量，对任意的t1＜t2＜…＜tn（n＞2），诸增量xit2－xit1，…，xitn－xitn－1相互独立.

设产品的阀值为确定值K，因此，产品tj时刻的可靠度可以表示为

式中：Φ（·）为正态分布函数，Φ（·）＝可得

μtj，σtj可以通过tj时刻的退化测量值进行估算，即其估算值为

于是式（1）和式（2）可写为

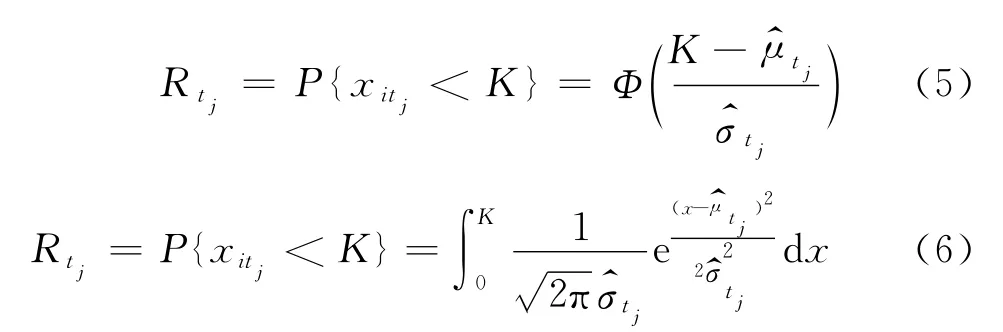
通过式（6）计算得到的是tj时刻在确定失效阀值的可靠度Rtj，对n个测量点依次计算得到数据｛（tj，Rtj），j＝1，2，3，…，n｝，假设产品的可靠度数据点集分布函数服从Weibull分布（由于Weibull能够根据不同参数表示不同形状分布，可以更确切地通过｛（tj，Rtj），j＝1，2，3，…，n｝点拟合曲线），则产品随时间变化的可靠度为

式中：t为时间；λ和β分别为Weibull分布的尺寸参数和形状参数，λ＝eγ／β，γ为计算λ的过渡参数.

文献［11］给出了利用点集（tj，Rtj）和最小二乘法估算参数λ和β方法为

式中：yj＝ln（－ln（Rtj））；τj＝ln（tj）.

利用式（8）求解出β和γ，即可求出λ.

2 模糊阀值的定义

2.1 隶属函数的定义

模糊理论和经典理论最大的区别是认为某个集合A的子集中的元素u不能明确说明是与否，而只能说明属于该子集的程度——隶属度，相应的函数称为隶属函数.

模糊子集是指：在论域U中对于任意的u∈U，指定一个数称为u对的隶属程度，即有

2.2 模糊阀值的定义

传统观念认为：产品在设计及其失效判定时，往往采用一个固定值δ作为判据.若超过δ时，则产品发生失效.但是在实际的设计和检测中，若产品退化特征值未超过某个范围，如1.05δ时，则认为产品是可以继续使用，因此，若将产品的失效阀值作为给定值则与实际不相符.但当产品的失效阀值为一个范围时，产品能够完成规定功能的概率将如何确定？换言之，选用一个合适的阀值作为产品失效的判定条件是非常困难的，这种亦此亦彼的特点反映出失效阀值的模糊性.针对这个难题，本文引入模糊失效区间，利用相对于模糊区间的隶属度代替固定阀值，计算产品在性能退化情况下的可靠性.

设在区间 ［δ1，δ2］中，由m个测试样品在tj时刻的退化量均值为，相对于模糊区间［δ1，δ］

2的隶属函数定义为，即

将式（9）代入式（6）得：

（1）当样品在tj时刻的退化均值在［0 ，δ1］时，可靠度公式为

（2）当样品在tj时刻的退化均值在［δ1，δ2］时，可靠度的模糊阀值为

依次对n个测量点进行计算，得到基于模糊阀值的产品性能退化数据的可靠度点集，将点集代入式（8）求得产品可靠度估计参数，将参数代入式（7），求得产品的可靠度计算公式.

3 工程算例

文献［11］利用威布尔分布结合常规的退化方法对产品退化试验的数据进行分析，退化量随时间的变化情况如图1所示，产品退化试验数据如表1所示，测试样品量为7，测量次数为5，各测量时刻为15，45，120，150，180h.在对产品的退化试验时，由于测试环境、测试人员、测试设备以及对试验数据的处理过程中方法等因素，引起对试验数据的随机性、模糊性，因此，利用基于模糊理论的方法对数据进行处理，能够反映试验过程的这些特点.

图1 退化量随时间变化的曲线Fig.1 Variation of time curve with degradation amount

表1 测量的退化数据Tab.1 Measuring the degradation data

失效阀值的模糊区间为［8.500，8.925］，隶属函数选降半型，即为

利用表1中退化数据，带入式（3）和式（4）中计算分别得到各个时刻的均值和方差，然后将方差和均值代入式（6），求得固定阀值情况下的时刻的可靠度，将方差和均值代入式（10）或式（11），算得在模糊阀值情况下，各个时刻的可靠度，如表2所示，

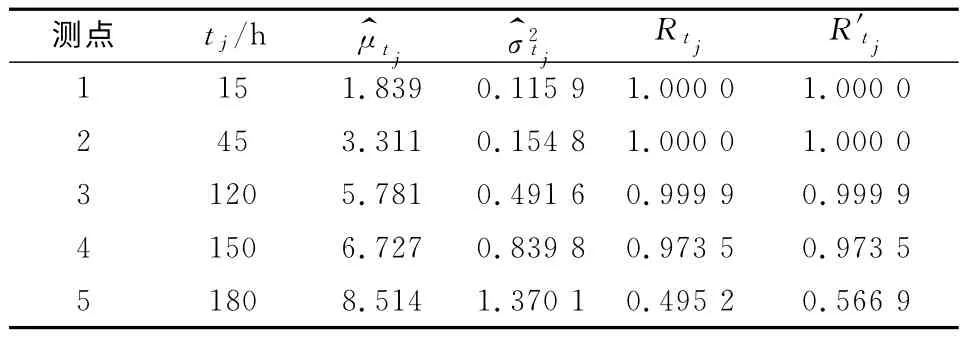
表2 各个测量点的均值及方差Tab.2 Mean and variance of each measuring point

利用表2中模糊阀值算得的各个时刻的可靠度数据并且参考文献［11］，代入到式（8）和式（7）拟合得到产品的可靠度计算公式为

当t＝180h时，失效概率为F（t）＝0.539 4，而文献［11］利用传统的方法的求解结果为0.544 2，显然偏高.两种方法的比较见图2.

图2 两种方法的比较Fig.2 Comparison of two methods

4 结论

（1）本文针对产品的失效阀值具有模糊性的特点，在利用退化失效数据对产品进行可靠性分析时，引入模糊区间代替固定的失效阀值，避免了固定阀值一刀切的特点，使得理论研究与实际情况更接近.

（2）通过采用模糊阀值方法对文献［11］的实例的分析，可以看出传统的固定阀值计算方法偏于保守，尤其是当测试样品的均值超过固定阀值的时候

（3）从图2分析可以看出，在模糊阀值情况下，产品的失效概率比固定阀值的失效概率偏小

［1］KIMY S，KOLARIK W J.Real－time conditional reliability prediction from on－line tool performance data ［J］.International Journal of Production Research，1992，30（8）：1831－1844.

［2］周东华，徐正国.工程系统的实时可靠性评估与预测技术［J］.空间控制技术与应用，2008，34（4）：3－9.ZHOU Donghua，XU Zhengguo.A survey on real－time reliability evaluation and prediction techniques for engineering systems［J］.Aerospace Control and Application，2008，34（4）：3－9.

［3］华城，张庆，徐光华，等.动态概率模型跟踪性能退化的实时可靠性评估方法［J］.西安交通大学学报，2010，44（1）：46－50.HUA Cheng，ZHANG Qing，XU Guanghua，et al.Real－time riability assessment method based on performance degradation tracked by dynamic probability model［J］.Journal of Xi’an Jiaotong Universty，2010，44（1）：46－50.

［4］赵炤，董豆豆，周经伦，等.基于贝叶斯方法的退化失效型产品实时可靠性评估［J］.国防科技大学学报，2007，29（6）：116－120.ZHAO Zhao，DONG Doudou，ZHOU Jinlun，et al.Real－time reliability evaluation for degradation failure product based on Bayes method［J］.Journal of National University of Defense Technology，2007，29（6）：116－120.

［5］张永强，冯静，刘琦，等.基于Poisson－Normal过程性能退化模型的可靠性分析［J］.系统工程与电子技术，2006，28（11）：1775－1778.ZHANG Yongqiang，FENG Jing，LIU Qi，et al.Reliability analysisbased on performance degradation model of compound Poisson－Narmal process ［J］.Sysrems Engineering and Electronics，2006，28（11）：1775－1778.

［6］潘玉娜，陈进，李兴林.基于模糊C－均值的设备性能退化评估方法［J］.上海交通大学学报，2009，43（11）：1794－1797.PAN Yuna，CHEN Jin，LI Xinglin.FuzzyC－means based equipment degradation assessment［J］.Journal of Shanghai Jiaotong University，2009，43（11）：1794－1797.

［7］HUANG R Q，XI L F，Li X L，et al.Residual life pre－dictions for ball bearings based on self－organizing map and back propagation neural network methods［J］.Mechanical Systems and Signal Processing，2007，21：193－207.

［8］YAN J H，LEE J.Degradation assessment and fault modes classification using logistic regression ［J］.Journal of Manufacturing Science and Engineering Transactions of the ASME，2005，127：912－914.

［9］OCAK H，LOPARO K A，DISCENZO F M.Online tracking of bearing wear using wavelet packet decomposition and probabilistic modeling：a method for bearing prognostics［J］.Journal of Sound and Vibration，2007，302：951－961.

［10］孙中泉，赵建印.Gamma过程退化失效可靠性分析［J］.海军航空工程学院学报，2010，25（5）：581－584.SUN Zhongquan，ZHAO Jianyin.Stochatic Gamma process degradation failure analysis［J］.Journal of Naval Aeronautical Engineering Institute，2010，25（5）：581－584.

［11］赵建印.基于性能退化数据的可靠性建模与应用研究［D］.长沙：国防科学与技术大学，2005.ZHAO Jianyin.Study on reliability modeling and applications based on performance degradation［D］.Changsha：National University of Defense Technology，2005.

［12］马纪明，詹晓燕.具有随机退化特性的柱塞泵性能可靠性分析［J］.机械工程学报，2010，46（14）：189－193.MA Jiming，ZHAN Xiaoyan.Performance reliability analysis of apiston pump affected by random degradation［J］.Journal of Mechanical Engineering，2010，46（14）：189－193.