橡胶双层减振与隔振系统冲击响应研究

张 志，张兆会，董 森，王泽锋，武 力，张凯胜，曹剑中

随着航天技术的不断发展，对航天产品的可靠性要求越来越高，而抗冲击性能是其中一项重要的指标。目前，适用此环境的减振系统大多采用橡胶减振系统，橡胶减振系统可以满足航空航天及国防等领域的高温、高压、高真空、超低温、腐蚀性介质等恶劣的工作环境［1－3］。橡胶减振器是目前国内外使用较多的减振形式，已有的文献中［10－11］对不同特性及结构形式的橡胶减振器的动态特性进行了分析与计算。金属橡胶减振器抗冲击是通过减振器的变形，把急剧输入的能量存储起来，冲击过后系统自由振动把能量释放出来［4］。

在航天领域，要求设备在三维方向都须具备较好的抗冲击能力，而目前采用的双层减振与隔振结构大多只在一个方向具有抗冲击的能力［5－7］。此外，在已有的研究中，加速度冲击量级都很小，基本都在1 000 g以下［7－9］，这远远不能满足航天产品的要求。

本文研究了一种用橡胶减震器组成的双层减震系统，并通过冲击实验证明此系统在8 000 g的加速度冲击下可以可靠的工作，同时，也为以后航天设备的可靠性设计提供了经验。

1 双层减振与隔振结构

1.1 双层减振与隔振系统模型［6，9］

本文中设计的双层减振与隔振系统为非线性力学模型，其力学模型如图1所示。

图1 双层减振系统模型Fig.1 The model of double-deck isolation system

图中，m和m2是上层质量和下层质量，x1、x2和 x3分别为基础、上层质量和下层质量的位移，在t=0时其初始条件为x1=x2=x3=0。由图1可建立系统的运动方程组为:

取相对位移 Y=x3－x2，Z=x3－x1，方程组(1)变为:

上述分析中，主要针对橡胶减振器的理论分析。在实际应用中，减振器的结构形式及其安装数量和位置对设备的抗冲击能力也有较大影响。本文设计的双层减振结构如图3所示。

图3 双层减振系统结构Fig.3 The structure of double-deck isolation system

其中:L为双层减振系统的上层质量与下层质量之比，F为上层刚度与下层刚度之比，n为减振器的非线性常数。

针对橡胶减振器，根据已有的研究成果，主要有以下几个因素影响系统的抗冲击性能。

(1)上下层质量比和刚度比的影响。通过优化上下层质量比和刚度比可以得到上层质量的最优的加速度响应和位移响应。

(2)阻尼的影响。综合考虑，减振系统的阻尼一般取0.3～0.5 为最佳。

1.2 设计实例

研究中使用的橡胶减震器结构如图2所示，减振器结构为对称结构，在X、Y、Z三个方向都有抗冲击能力。

单层干燥（6 h）、双层干燥（6 h）、三层干燥（8 h） 的最终样品水分含量分别9.33%，7.77%和8.68%，双层物料最终湿基含水量最低且各层物料最终湿基含水量无显著差异（p＞0.05），物料均匀性最好。

图2 橡胶减振器结构Fig.2 The structure of rubber damper

下层减振结构采用四个橡胶减振器，橡胶减振器通过连接螺钉将外壳安装在底板上，通过拧紧螺母使橡胶减振器在Z向产生一定的压缩量。同时，由于连接螺钉直径大于减振器的内孔，因此，减振器在X、Y方向也有一定的压缩量。由此可知，这种结构形式在X、Y、Z三个方向都有抗冲击的能力。

同理，上层减振结构同样采用四个橡胶减振器，通过连接螺钉将基板安装于外壳上，而设备中的关键器件都是分布于基板上，这样也就使设备中的关键器件受到最大限度的缓冲保护。实验证明，这种双层减振结构具有良好的抗冲击能力。

2 双层减振与隔振系统仿真分析

针对上述双层减振与隔振结构进行了仿真分析。分析方法如下:

(1)首先分别建立单层减振与隔振及双层减振与隔振的有限元模型，并对模型进行适当简化;

(2)分别将两个有限元模型导入有限元分析软件Ansys中;

(3)将冲击试验的试验条件作为输入条件输入到Ansys软件中分别对两个模型进行计算;

(4)计算完成后，分别提取模型中的关键点的冲击响应值，并对两种模型的响应值进行对比分析，从而得出结论。

图4 双层减振与隔振系统有限元模型Fig.4 The finite element model of double-deck vibration isolation system

表1 基板中心点的冲击响应值Tab.1 The impact response value of center point at substrate

由表1可知，双层减振与隔振系统基板中心点的冲击响应值明显小于单层减振与隔振系统，即双层减振与隔振系统的减振与隔振效果明显优于单层减振与隔振系统。

3 加速度冲击实验

为了验证本文设计的双层减震结构的抗冲击能力，进行了大量级的加速度冲击实验。实验装置如图5所示。

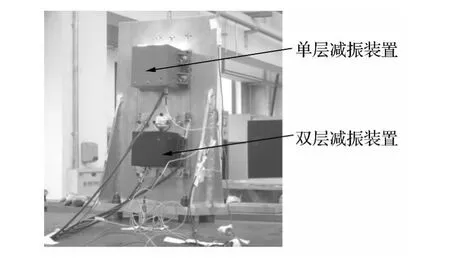
图5 冲击试验装置Fig.5 Experimental devices of shock response

图5 中，为了比较双层减振结构与单层减振结构冲击响应谱的差别，将两者安装在同一振动夹具上。表2为冲击实验条件。

表2 冲击试验条件Tab.2 Experimental conditions of shock response

实验时，在X、Y、Z三个方向上每个方向冲击两次，并测量冲击方向的响应。实验测得的X、Y、Z三个方向上的冲击响应谱如图6～图8所示。

图6～图8中，ch1为振动夹具上传感器的冲击响应谱曲线，ch2为两层减振结构的冲击响应谱曲线，ch3为单层减振结构的冲击响应谱曲线，由图可得到以下结论:

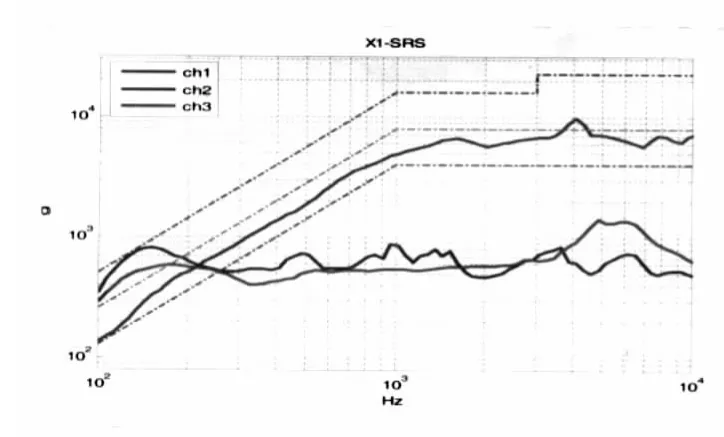
图6 Z方向冲击响应谱Fig.6 Shock response spectrum on Z axis

图7 Y方向冲击响应谱Fig.7 Shock response spectrum on Y axis

图8 X方向冲击响应谱Fig.8 Shock response spectrum on X axis

(1)图6～图8表明，在8 000 g的加速度冲击下，经过下层橡胶减振器后，冲击响应衰减为3 000 g左右，即下层减振器可以吸收大部分的冲击能量。

(2)由图6～图8可知，当频率小于3 000 Hz时，Y向与Z向的响应曲线差异较大，X向的响应曲线虽有差异，但差异较小。说明在低频段，双层减振与隔振系统在Y向与Z向的减振效果较好，而在X向的减振效果不明显。当频率高于3 000 Hz时，双层减振结构的加速度冲击响应谱值在X、Y、Z三个方向上都比单层减振结构小1 000 g左右，即双层减振结构在高频段的抗冲击能力优于单层减振结构，结论与上述仿真分析结果基本一致。

(3)图4中，双层减振结构的下层安装四个橡胶减振器，由于减振器在X、Y方向的结构相同，单个减振器在X、Y方向的抗冲击能力也一样。所以，引起X、Y方向冲击响应谱不同的因素主要取决于橡胶减振器安装的跨度，由图可知，Y向的跨度为128 mm，X向的跨度为52 mm。由图7、图8可知，当频率大于2 000 Hz时，Y向的冲击响应谱值明显小于X向，即适当增加橡胶减振器的安装跨度可以提高系统的抗冲击能力。

4 结论

经过以上的分析，在大量级的加速度冲击下(如8 000 g)，可得到以下结论:

(1)在8 000 g冲击下，下层的橡胶减振器可以吸收大部分的冲击能量。当频率小于3 000 Hz时，二层减振结构与单层减振结构的冲击响应谱大致相同;当频率大于3 000 Hz时，双层减振结构抗冲击能力明显优于单层减振结构。

(2)当使用橡胶减振器进行减振时，增加橡胶减振器的安装跨度可以提高系统的抗冲击能力。

(3)经试验验证，设计的双层减振结构经历六次8 000 g加速度冲击后能够正常工作，这对航天设备的可靠性设计具有重要的意义。

［1］切戈达耶夫等.金属橡胶构件的设计［M］.李中郢译.北京:国防工业出版社，2000.

［2］姜洪源，夏宇宏，敖宏瑞，等.航空发动机用特种金属橡胶构件的应用［J］.研究燃气涡轮实验与研究，2003，16(3):1－5.JIANG Hong-yuan， XIA Yu-hong，AO Hong-rui，et al.Research on the application of special metal rubber components used in aero engine［J］.Gas Turbine Experiment and Research，2003，16(3):1 －5.

［3］郭宝亭，朱梓根，崔荣繁，等.金属橡胶材料的理论模型研究［J］.航空动力学报，2004，19(3):314－319.GUO Bao-ting， ZHU Cui-gen， CUI Rong-fan， et al.Theoretical model of metal-rubber［J］.Journal of Aerospace Power，2004，19(3):314 －319.

［4］敖宏瑞，姜洪源，闫 辉，等.基于小波变换的金属橡胶干摩擦系统阻尼识别［J］.机械设计，2004，21(7):27－30.AO Hong-rui，JIANG Hong-yuan，YAN Hui，et al.Wavelet transformation based damping identification for metal rubber dry friction system［J］.Journal of Machine Design，2004，21(7):27－30.

［5］王志伟，武冬雁.矩形脉冲激励下正切型非线性包装系统的冲击响应［J］.振动与冲击，1999，18(3):48－51.WANG Zhi-wei， WU Dong-yan. The shock response of tangential nonlinear packaging system under the action of rectangular pulse［J］.Jouranl of Vibration and Shock，1999，18(3):48－51.

［6］高 德，卢富德.两自由度正切非线性系统的冲击响应研究［J］.哈尔滨商业大学学报，2010，26(6):748－752.GAO De，LU Fu-de.Study of shock response spectra surface under half-sine pulse of two-degree of freedom tangent nonlinear system［J］.Journal of Harbin University of Commerce，2010，26(6):748－752.

［7］严东晋，唐德高，钱七虎.爆炸冲击震动下双层线性隔震体系的隔震性能［J］.振动工程学报，2001，14(3):339－344.YAN Dong-jin， TANG Deg-ao， QIAN Qi-hu. Isolation properties of double mass-spring system under blast shock and vibration［J］. Journal of Vibration Engineering，2001，14(3):339－344.

［8］李红刚，彭 旭.具有刚度非线性双层隔振系统冲击响应数值分析研究［J］.噪声与振动控制，2007，27(1):21－26.LI Hong-gang，PENG Xu.Shock response of two degrees of freedom isolation system with isolator of non-linear stiffness［J］.Journal of Noise and Vibration Control，2007，27(1):21－26.

［9］黄秀玲，王 军，卢立新，等.三次非线性包装系统关键部件冲击响应影响因素分析［J］.振动与冲击，2010，29(10):179－181.HUANG Xiu-ling，WANG Jun，LU Li-xin，et al.Factors influencing shock characteristics of a cubic nonlinear packaging system with critical component［J］.Journal of Vibration and Shock，2010，29(10):179－181.

［10］潘孝勇，谢新星，上官文斌.变振幅激励下的液阻橡胶隔振器动态特性分析［J］.振动与冲击，2012，31(1):144－149.PAN Xiao-yong，XIE Xin-xing，SHANGGUAN Wen-bin.Dynamic properties analysis for a hydraulic rubber isolator under excitations with different amplitudes［J］.Journal of Vibration and Shock，2012，31(1):144－149.

［11］吴礼刚，段小成，黄 兴，等.半主动液阻型橡胶隔振器动态性能测试与计算分析［J］.振动与冲击，2011，30(4):33－37.WU Li-gang，DUAN Xiao-cheng，HUANG Xing，et al.Test and calculation for dynamic performances of a semi-active engine mount［J］.Journal of Vibration and Shock，2011，30(4):33－37.