混凝土防爆墙对爆炸冲击波传播的影响

张千里，张 耀，年鑫哲

爆炸冲击波是常规弹药爆炸对防护结构产生破坏效应的主要因素之一，是防护结构设计时必须考虑的重要方面，尤其是对于构筑半地下和地表的防护结构。当炸药在防爆墙周围爆炸时，空气冲击波对墙体结构的爆炸荷载和冲击波绕过墙体并在墙体的后部形成环流超压，对建筑物的破坏及人员的损伤是一个迫切需要解决的问题。国外 Schleyer等［1］，Langdon 等［2］分别通过试验和数值模拟研究了冲击波压力峰值在不锈钢面板上的分布规律。近年来，国内对此问题进行了研究。郝莉等［3］采用算子分裂格式，运用体积份额法处理多介质界面，用三维数值模拟程序MMIC3D模拟计算三维空中爆炸的爆源附近和爆炸场中冲击波流场的发展规律，分析比较了挡墙位置、形状，对挡墙后爆炸冲击波的影响。王仲琦等［4］采用二维多流体网格法，对有防护挡墙的爆炸形成的空气冲击波作了计算分析。李鑫等［5］分析了炸药在自由空气中，刚性地面，沙土地面上起爆情况下，对不同方向超压分布的影响，研究了冲击波遇到挡墙时，迎爆面的超压和比冲量分布及冲击波绕射之后挡墙后方的超压分布的影响。宁建国等［6］通过自行编制的SMMIC程序模拟了爆炸点周围有和无防护挡墙的二维爆炸场的初始发展过程和绕过障碍物的情况。王飞等［7］利用ALE算法和炸药爆轰产物的JWL状态方程，对空气冲击波绕过障碍物的环流现象进行了数值模拟，得到了在爆源附近有障碍物的爆炸场初始发展和环流的情况。洪武等［8］分析了冲击波在垂直墙体、迎向以及背向炸药倾斜墙体上的反射、绕流以及荷载分布规律，总结出了不同工况时墙体荷载计算方法。蒋志刚等［9］分析了防爆墙体在水平均布冲击波荷载作用下绕墙趾产生刚体转动，得到了指数衰减荷载和瞬时冲量荷载作用下墙体转动线性微分方程的解析解和倾覆稳定系数计算公式。在实验方面，张六一等［10］，曾容生等［11］对冲击波绕过山体进行了大量的试验研究得到了丰富的试验数据并推导出一些有重要参考价值的公式。穆朝民等［12］采用试验的方法，对爆炸冲击波作用于防爆墙及绕过墙体的规律进行了研究，采用压力传感器测压，获得了防爆墙前后不同距离的压力波形。

本文在以上研究基础上，进行了抗爆防护墙试验，采用压力传感器技术获得了防爆墙前后不同距离的压力。同时采用ALE算法，建立包括空气、炸药、防爆墙在内的多物质模型，分析了爆炸冲击波遇到挡墙时的压力变化及环流绕射作用，为进一步的理论及实验研究提供有益参考。

1 实验研究

1.1 试验结构

选择平整开阔场地，浇注长9 m、高2.5 m、厚0.4 m混凝土防爆墙(见图1)。在距墙底0.22 m、1.31 m、2.4 m处预设塑料套管，并布设压力传感器(见图2)，传感器与墙面平齐。在防爆墙后，距墙2 m、4 m、6 m处布设压力传感器，试验布置图(见图3)。A为起爆点，B、C、D、E、F、G、H分别为压力传感器。装药量分别为5 kg，20 kg。

图2 压力传感器Fig.2 Pressure sensor

1.2 量测系统及设备

数据采集采用DH5939N高速数据采集记录仪(见图4)，这是一套集采集、分析、结果输出为一体的多用途智能化的测量系统。该设备的采样频率为500 kHz，分析频率195 kHz，采集纪录长度为1M字节，采集通道为24，触发方式为24通道单通道信号触发，灵敏度为130 mV/EU;应变放大器型号DH3842，该放大器的特点是质量轻，体积小，抗震性能好，便于携带和搬运，频带宽;压力传感器型 CA－YD－205，灵敏度为132.6 Pc/MPa。

2 试验结果及分析

2.1 实验数据

对防爆墙进行了多次试验，得到超压时程曲线如图所示。图5为5 kg TNT在距防爆墙3 m处爆炸，各个测点的压力时程。图6为20 kg TNT在距防爆墙3 m处爆炸，各个测点的压力时程。

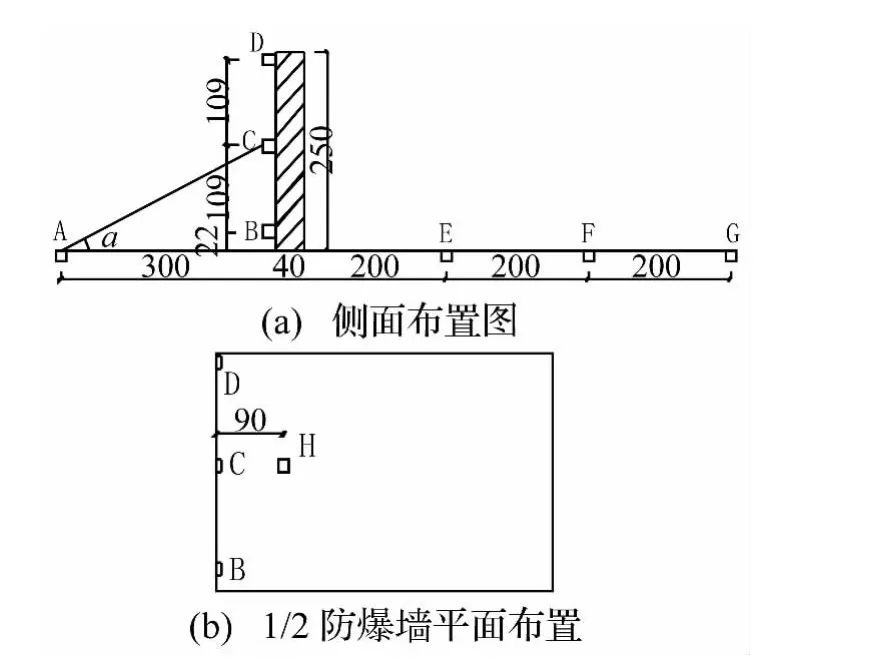
图3 试验布置图(单位:cm)Fig.3 Test arrangement

图4 数据采集记录仪Fig.4 Data acquisition recorder

2.2 实验分析

由图5(a)及图6(a)可看出，炸药爆炸后，爆轰产物猛烈膨胀，压缩周围空气介质，并推动周围空气向外运动。经过很短的时间，进行成压力突跃的阵面，即该强扰动以激波形式在空气中传播。爆轰产物的膨胀不断地供给冲击波能量，推动冲击波以一定的速度向前传播。随着爆轰产物的膨胀，它占有的体积越来越大，能量密度就逐渐变小，因而爆轰产物的压力、温度和运动速度不断下降，随之冲击波能量也逐渐减小，当爆轰化产物内的压力下降到与大气压力相近时，就不再膨胀，以后冲击波脱离爆轰产物向前运动而在尾部形成稀疏区，稀疏区中的压力低于大气压力。我们把超过大气压力的瞬时压力称为超压，在某给定位置上超压的最大值称为超压峰值;低于周围大气压力的瞬时压力称为负压。超压是突然增大，且峰值较大;而负压是缓变的，峰值相对较小。测点B、C、D是沿墙体高度方向的三个测点，在0.51 s时，三点几乎同时达到超压峰值，然后迅速下降，其中测点C峰值最大，其次是点B，D最小，即随着高度的增加超压峰值先增大后减小。设起爆点到墙迎爆面的距离与起爆点到墙体某点距离之间的夹角为a，随着a的增大压力峰值先增大后减小，故存在临界角度。冲击波作用于墙体，墙面附近形成密集的空气层，一部分产生冲击波正反射，一部分沿壁面向上运动。由图5(b)及图6(b)可以得知作用于墙迎爆面反射超压比墙后的最大超压环流大1个数量级，说明防爆墙对冲击波有消波作用，且5 kg装药的消波作用比较明显，但环流超压正相作用时间要比墙迎爆面上的冲击波超压正相作用时间大2～3倍(见表1)。

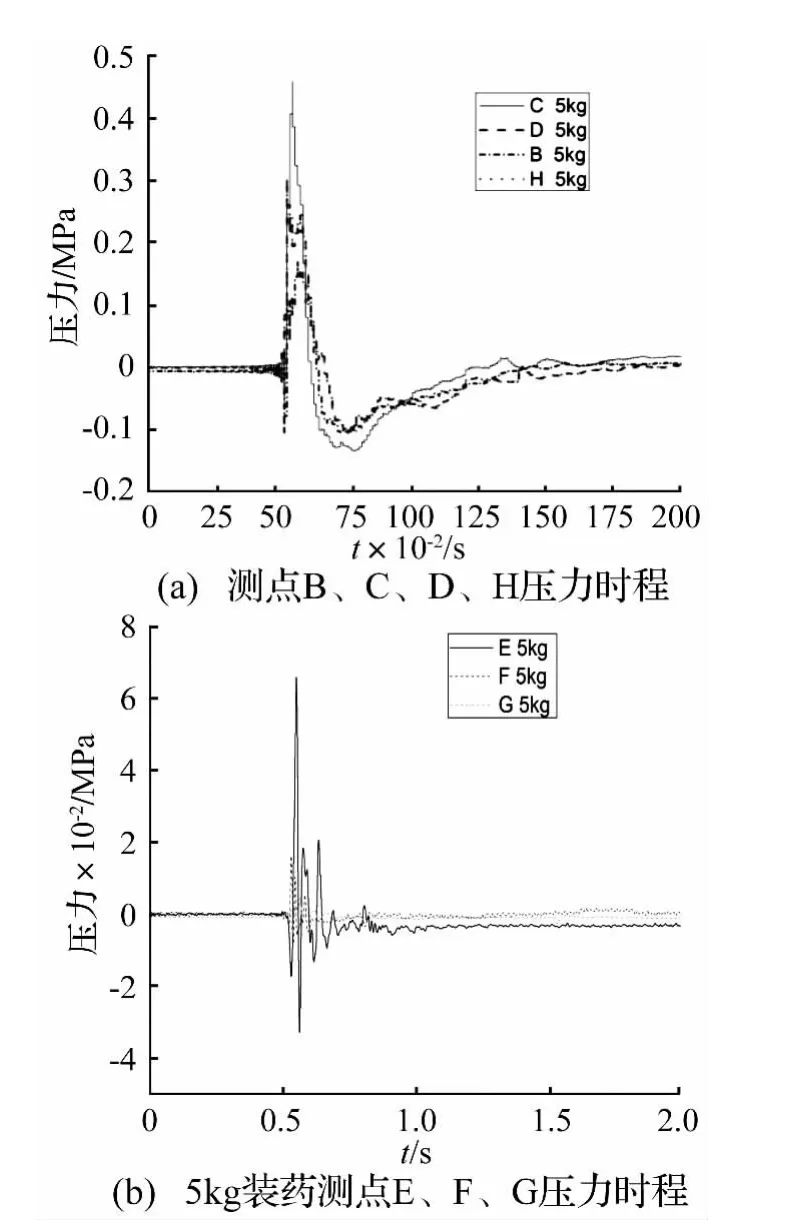
图5 5 kg装药压力时程Fig.5 Pressure time of 5 kg charge

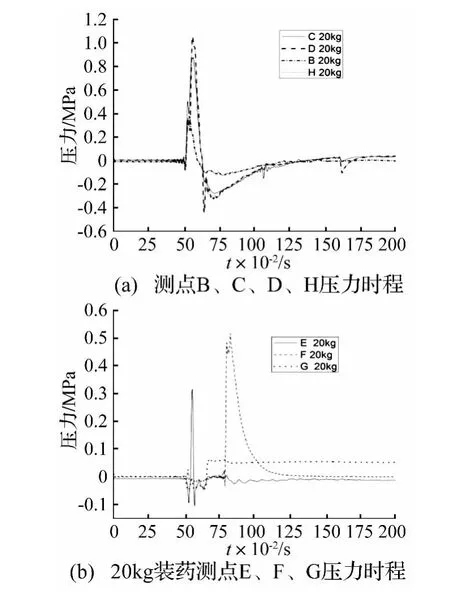
图6 20 kg装药压力时程Fig.6 Pressure time of 20 kg charge

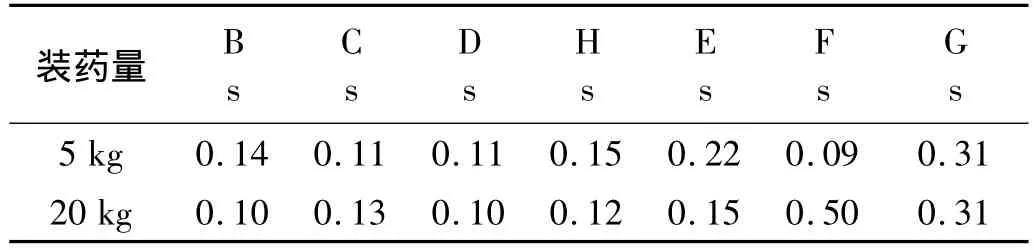
表1 超压正相作用时间Tab.1 Time of overpressure positive phase

表2 试验各测点峰值压力Tab.2 Peak pressure of test points

表2可以看出:影响墙体荷载的主要因素有装药重量、墙体高度、墙体后方的环流。环流超压与装药量成正比，与爆心距离成反比，测点F即墙后4 m时，环流超压峰值大于测点E、G，这是因为在此位置环流与地面形成了马赫反射，反射冲击波研究表明［13］:在 a＜40°的情况下，最大环流超压一般发生在墙背后1.5～2.5倍墙高处。

3 数值模拟

3.1 控制方程

无粘、无热传导、忽略体力的三维非定常可压缩流体的偏微分方程组［14］为:

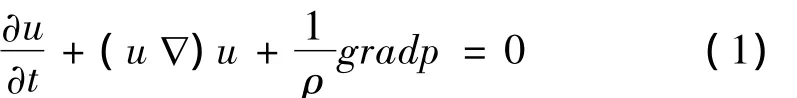
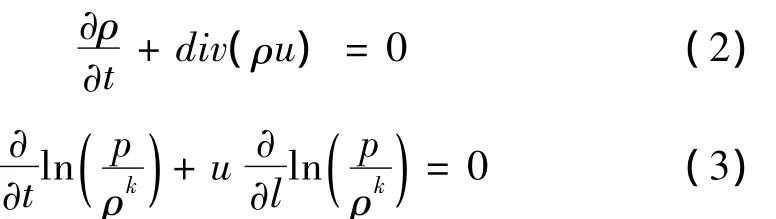
上述方程组加状态方程和间断面条件构成控制方程。间断面处的Rankine-Hugoniot条件［14］为:

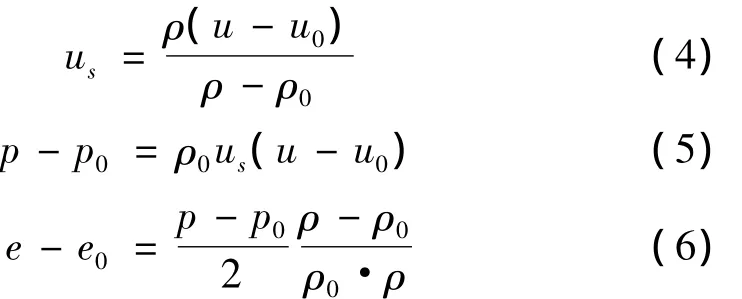
上述公式中字母符号的含义参见相关文献，此处从略。

3.2 状态方程

(1)TNT炸药状态方程采用JWL状态方程［14］，其表达式为:

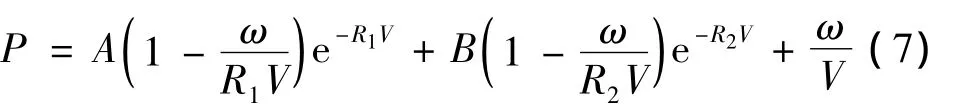
式中:P、E、V、分别表示爆轰产物的压力，单位体积的内能被和比容(即单位体积装药产生爆轰产物的体积)。状态方程中的系数 A、B、R1、R2、ω 为描述 JWL方程的五个独立物理常数。本文数值计算中A=3.74e11 Pa，R1=4.15，R2=0.95，E=0.07 cm2·μs－2，w=0.03。炸药密度取 1.63 g·cm－3，爆速为6 930 m·s－1。

(2)空气线性多项式状态方程［10］:

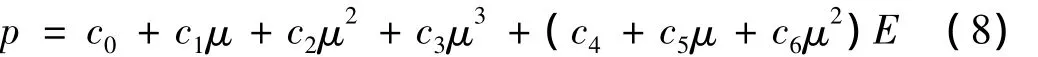
式中:p为空气压力:μ =ρ/ρ0－1，ρ为当前密度，ρ0为空气压力:E 为材料的内能;c0、c1、c2、c3、c4、c5、c6为状态方程参数。

3.3 计算模型

数值模拟采用LS-DYNA3D软件［15］，利用 ALE算法和JWL状态方程研究爆炸冲击波作用于墙体和在墙后的绕流问题。空气将炸药和防爆墙包围住，炸药位于墙体正前方。其中空气和炸药均采用欧拉单元，防爆墙采用拉格朗日单元，空气为可流出边界。分别将5 kg、20 kg TNT炸药放在防爆墙的中轴线上，距防爆墙3 m。数值模拟严格按照实验模型进行建模，模型长12.6 m，宽4 m，高4.5 m。本次数值模拟利用对称性取1/2结构模型，5 kg TNT时，炸药 12个单元，空气226 898个单元，防爆墙3 100个单元。20 kg TNT时，炸药48个单元，空气243 384个单元，防爆墙3 224个单元。

3.4 计算结果和分析

距离爆心3 m处，计算所得墙体上反射冲击波超压与墙后环流超压结果如表3。比较表2可知，计算值与实验数据基本一致，反映了数值模拟计算的正确性。

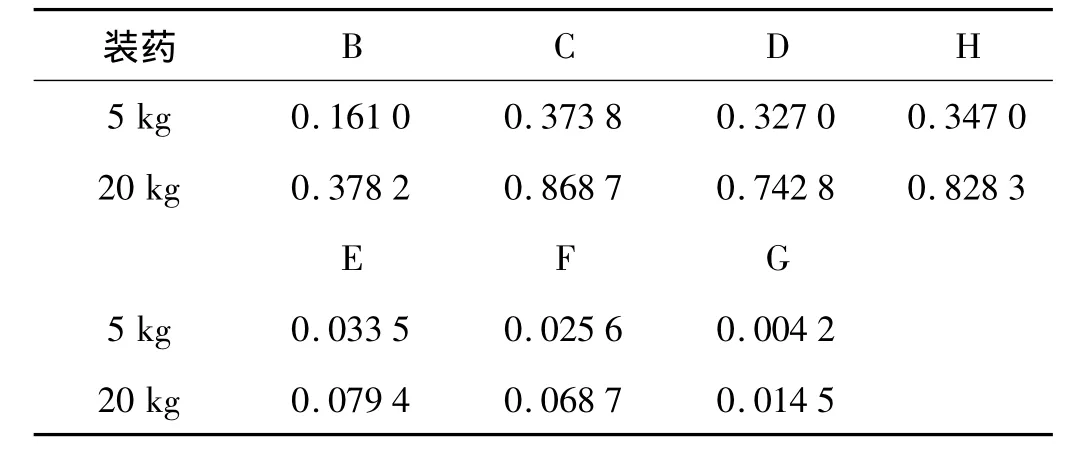
表3 数值模拟各测点压力峰值Tab.3 Peak pressure of test points of numerical Simulation

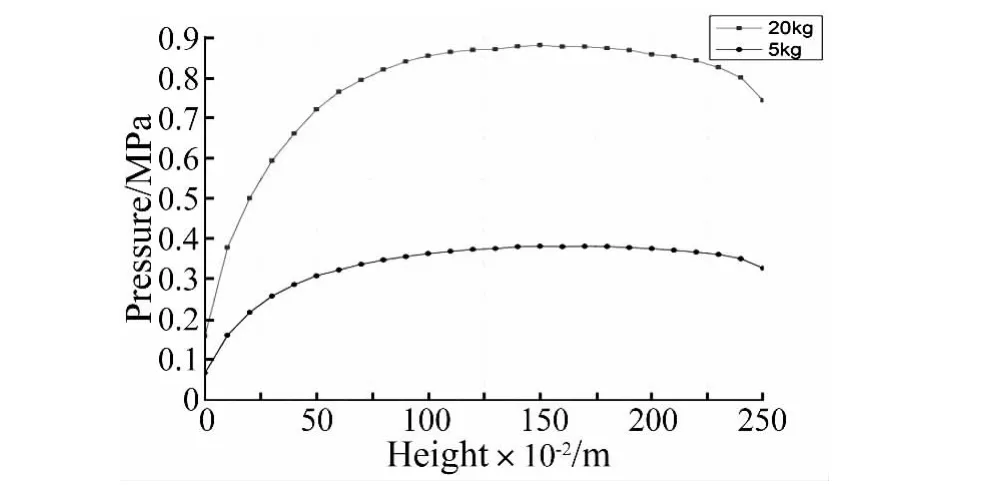
图7 前墙压力峰值Fig.7 Peak pressure of the front wall

图7 给出了沿墙体高度方向压力峰值的变化情况。由图可看出压力峰值先迅速上升，在缓慢下降，与试验相一致。1.6 m～1.8 m时，压力峰值达到最大，而此时计算a=31°，故a=31°时压力变化的临界位置。当a＜31°时，超压峰值随墙体测点的增高而增大，即成正相关;当31°＜a＜40°时，超压峰值随墙体测点的增高而减小，成负相关。与表2的实验结果相比大致符合，其中20 kg装药时，墙高1.5 m以内的结果比较相近，超过1.5 m时，实验结果比模拟结果衰减的更快，这是由于试验场地可是无限自由场，冲击波压力峰值在自由场中衰减的较快。

根据两种装药爆炸在墙背后产生的环流与地面作用，形成马赫波，绘制图8。图8给出了墙后各点的峰值压力，由图可知随着距离的增加，墙背后最大环流超压峰值先稍微增大，随后逐渐减小，5.5 m时，减小的速率明显加快。5 kg TNT时，峰值压力出现在，距墙背面3 m～3.5 m处;20 kg TNT时，峰值压力出现在，距墙背面3.5 m ～4 m 处。与相关研究［12～13］大致符合。其中20 kg装药时，点E、F、G的值比试验小得多，这是因为试验中冲击波在空气－土壤界面发生反射，且反射压力大于入射压力，而模型中未建立土壤有限元，使得压力衰减较快，且药量越大，现象越明显。

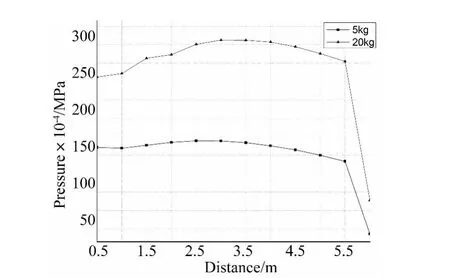
图8 墙后压力峰值Fig.8 Peak pressure after the wall

图9 给出了冲击波绕流逐步形成发展的基本过程［16］。可以看出，这些基本过程与物理图像基本符合。图9(a)～图9(f)分别代表冲击波与防爆墙作用的典型过程，不同的超压区用不同的颜色表示，并显示了压力分布曲线。图9(a)显示了以炸药为中心的爆轰产物的传播，而冲击波并不是以球面波的形式向外传播，这时因为药包的形状是立方体的集团装药。然而随着传播距离的增大，冲击波将以球面波的形式向外扩张。图9(b)显示冲击波刚到达障碍物，冲击波阵面处的气流质点与障碍物相遇的瞬时即被遏制，然后下一层的运动质点亦被阻止，停止向入射波传播方向运动，这是在障碍物附近出现高压静止区。迎爆面超压骤然增大，且在迎爆面附形成反射高压区(见表2，3正反射超压)。图9(c)显示迎爆面边缘以上的冲击波并未遇到障碍，相对于迎爆面中央附近的高压区，它就成为低压区。由此形成的压力差会引起空气流动和稀疏波的产生，亦即墙迎爆面处高压区中的空气向迎爆面边缘外低压区流动的同时，高压区的空气由边缘到内部逐渐受到稀释，这种稀疏状态由迎爆面外侧向中心的传播即是稀疏波。图9(d)显示了入射冲击波沿着壁面传播，密集层空气开始上流，稀疏波以当地音速向高压区内传播;壁正面处向上运动的空气，在其运动过程中由于受到壁顶部入射波后流动空气的影响而改变了运动方向。此时，迎爆面上的压力相对变化不再发生，而仅随入射波中压力的衰减逐渐减少到零。在a小于40°的条件下，墙背面环流超压最大值点的距离小于1.5～2.5倍墙高，这与试验基本一致，说明了数值模拟合理性。当环流没有把墙体包围住时墙体受的荷载最大。当完全把目标包围了后，在墙后5.0 m处环流与地面发生了马赫反射，见图9(e)，此时环流超压达到最大值，且计算值与试验测量值基本一致。在形成马赫反射后又有后续越过墙体的弱平面波与马赫反射波共同存在。数值模拟基本上反映了爆炸冲击波作用在防爆墙上载荷以及爆炸冲击波绕过防爆墙环流超压变化的规律，在环流与地面作用形成马赫反射波后方，有弱的平面入射波存在，且在一定距离内，此平面波有追赶加强的趋势，如图9(f)所示。

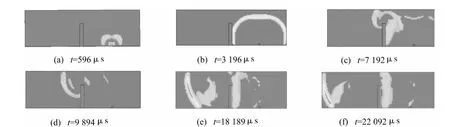
图9 爆炸冲击波传播Fig.9 Blast wave propagation

4 结论

(1)墙后的环流超压经历一个先正相，后负相的阶段，其负压峰值与作用时间均小于正相。

(2)作用于墙迎爆面反射超压一般要比墙后的最大环流超压大1个数量级，但环流超压正相作用时间要比墙迎爆面上的冲击波超压正相作用时间大2～3倍。

(3)墙后环流超压从墙后开始，经历了由小变大再变小的阶段。环流超压的影响因素主要有装药量，墙高，背爆面距离墙后超压点的距离。当a＜31°时，超压峰值随墙体测点的增高而增大，即成正相关;当31°＜a＜40°时，超压峰值随墙体测点的增高而减小，及成负相关。

(4)爆炸冲击波绕过墙后，在a＜40°的条件下，形成环流后，背爆面距离环流超压最大值点的距离小于1.5～2.5倍墙高，环流与冲击波作用形成马赫波，在形成马赫反射后又有后续越过墙体的弱平面波与马赫反射波共同存在。

［1］ Schleyer G K，Lowak M J，Polcyn M A，et al.Experimental investigation of blast wall panel under shock pressure loading［J］.International Journal of ImpactEngin-eering，2007，34:1095－1118.

［2］ Langdon G S，Schleyer G K.Deformation and failure of profiled stainless steel blast wall panels，PartⅢ:finite element simulations and overall summary［J］.International Journal of Impact Engineering，2007，34:988 －1012.

［3］郝 莉，马天宝.爆炸冲击波绕流的三维数值模拟研究［J］.力学学报，2010，42(6):1042 － 1048.HAO Li，MA Tian-bao. Three dimensional numerical simulation study on the flow of the explosion shock wave around the wall［J］.Chinese Journal of Theoretical and Applied Mechanics，2010，42(6):1042 － 1048.

［4］王仲琦，宁建国，赵衡阳.挡墙对远场爆炸效应影响的数值模拟研究［J］.爆炸与冲击，2000，20(1):87 － 91.WANG Zhong-qi， NING Jian-guo， ZHAO Heng-yang.Numerical simulation on 2D explosion field with the protective wall［J］.Explosive and Shock Wave，2000，20(1):87 －91.

［5］李 鑫，吴桂英，吴昊凯.挡墙对爆炸冲击波传播影响的数值模拟［J］.工程力学，2012，29(2):245 －250.LI Xin，WU Gui-ying，JIA Hao-kai.The numerical simulateon of explosion shock wave propagation subject to the retaining wall［J］.Engineering Mechanics，2012，29(2):245－250.

［6］宁建国，王仲琦，赵衡阳，等.爆炸冲击波绕流的数值模拟研究［J］.北京理工大学学报，1999，19(5):543－ 547.NING Jian-guo，WANG Zhong-qi，ZHAO Heng-yang.Study on theflow of the explosive shock wave around the wall numerical simulation［J］.Journal of Beijing Institute of Technology，1999，19(5):543－ 547.

［7］王 飞，朱立新，顾文彬，等.基于ALE算法的空气冲击波绕流数值模拟研究［J］.工程爆破，2002，8(2):13 － 16.WANG Fei，ZHU Li-xin，GU Wen-bin.Numerical simulateon of shock wave around－flow on basis of ALE algorithm［J］.Engineering Blasting，2002，8(2):13 － 16.

［8］洪 武，范华林，金丰年，等.刚性防爆墙迎爆面荷载计算方法研究［J］.工程力学，2012，29(11):228－235.HONG Wu，FAN Hua-lin，JIN Feng-nian，et al.Blast response of inclined rigid walls［J］.Engineering Mecha-nics，2012，29(11):228 － 235.

［9］蒋志刚，孔晓鹏，谭清华，等.土工防爆墙倾覆稳定性分析［J］.振动与冲击，2010，29(10):86－90.JIANG Zhi-gang，KONG Xiao-peng，TAN Qing-hua，et al.Overturn stability analysis of geotechnic-al explosion-proof walls［J］.Journal of Vibration and Shock，2010，29(10):86－90.

［10］张六一，周丰峻.核爆炸近区空气冲击波参数研究综述［J］.防护工程，1985，4:1 － 11.ZHANG Liu-yi，ZHOU Feng-jun.Overview of parameters in near zone of nuclear blast［J］.Protective Engineering，1985，4:1－ 11.

［11］曾容生，陈志林.上坡和下坡地形对冲击波的超压峰值影响的计算［J］.防护工程，1985，3:1 － 10.ZENG Rong-sheng，CHENG Zhi-lin. Calculation of plus grade and minus grade influence on overpressure peak［J］.Protective Engineering，1985，3:1 － 10.

［12］穆朝民，任辉启，李永池.爆炸冲击波对墙体绕射效应的研究［J］.力学与实践，2009，31(5):35 － 40.MU Zhao-min，REN Hui-qi，LI Yong-chi.Research into impact effect on wall and flow around wall of explosive shock wave［J］.Mechanics and Engineering，2009，31(5):35－40.

［13］穆朝民，王广勇.爆炸冲击波绕过墙体的数值模拟研究［J］.工程爆破，2008，14(2):16 － 19.MU Zhao-min， WANG Guang-yong. Study numerical simulation of explosive shock wave rounding wall［J］.Engineering Blasting，2008，14(2):16 － 19.

［14］ LS－DYNA Theoretical Manual(version 970).2003.

［15］ LS－DYNA User's Manual(Nonlinear Dynamic Analysis of Structures in Three Dimensions).

［16］叶序双.爆炸作用基础［M］.南京:解放军理工大学工程兵工程学院出版社，2003.