泥石流浆体冲击特性实验研究
2013-05-24何晓英唐红梅朱绣竹陈洪凯
何晓英,唐红梅,朱绣竹,陈洪凯
泥石流运动与冲击特性是泥石流减灾及沟谷地貌演化的重要基础理论问题,是深入认识泥石流形成、运动和成灾机制的基础。由于泥石流是固-液两相复杂介质,泥石流的冲击破坏来自于泥石流浆体的冲击和泥石流固相颗粒集中荷载的耦合[1],且其运动具有脉动性,因此,泥石流的运动特性和冲击荷载的确定多年来一直是泥石流动力学研究中最薄弱的环节[2]。
实验研究是实施泥石流运动学动力学研究的主要方法之一,便于科学探索影响泥石流运动与冲击众多因素中单个因子的贡献及多因子之间的相互作用规律。如针对泥石流流速与运动过程,很多学者[3-4]进行了理论与实验研究,得到泥石流流速的计算方法;Valentino等[5]进行了颗粒流水槽试验,采用摄像法记录了颗粒流形成及运动过程,并借助于离散元软件PFC 2D系统模拟了该试验,获取颗粒流冲出距离和冲击力频谱特性;Yang等[6]通过水槽试验探讨了泥石流流速与冲击特性,得到了泥石流表层流速与表层冲击力之间的关系;Wang等[7]通过泥石流浆体动力试验进行了粘性泥石流流变特性研究,认为泥石流属于典型粘弹性体,其储能模量与泥石流体中所含固体颗粒大小有关;Scheidl等[8]实施了小规模泥石流冲击特性模型试验,通过16组试验分析计算了泥石流的最大冲击力;Bugnion等[9]通过泥石流冲击模型试验测量泥石流冲击力,得到泥石流冲击速度为2~13 m/s;吴积善等[10]根据蒋家沟泥石流1974~1975年冲击力测试资料,得到泥石流冲击动压力的修正公式,通过实际观测将泥石流冲击力概化为锯齿形脉冲、矩形脉冲和尖峰形脉冲;张宇等[11]引入泥石流体微元概念,将泥石流冲击力作为非平稳信号,采用Hilbert变换进行时频处理确定冲击作用时间。
综上可见,目前关于泥石流运动与冲击特性的相关研究均侧重泥石流流速及小规模水槽试验,在实际沟谷内进行相关实验及对泥石流冲击信号的细观分析研究较少,对于泥石流的冲击特性的研究未系统考虑泥石流浆体粘度的影响,不能系统揭示泥石流运动与冲击。本团队[12]自2006年以来,针对沟谷泥石流,着眼其冲击特性,系统进行了考虑泥石流固液两相性的冲击特性研究,从固液两相流理论出发探讨了泥石流冲击力计算问题;针对天山公路K630泥石流,建立沟谷泥石流相似模型试验,发现泥石流阵流具有嵌套现象,强阵嵌套2~3次弱阵[13];建立泥石流冲击试验模型进行不同固相比、不同颗粒粒径的水石流冲击特性研究,通过水石流模型试验,发现随着固相比及颗粒直径增大,泥石流冲击荷载呈非线性增加,且颗粒粒径越大,冲击荷载概率密度分布曲线易出现多峰或极值现象[14-15];泥石流 90% 以上的冲击能量分布在小于0.195 Hz的低频部分,水石流在中高频段的冲击能量总体呈衰减分布[16]。本文在团队前述研究的基础上,修筑较大尺度的泥石流沟实验模型,仅实施泥石流浆体冲击特性模型实验,探索实验条件下泥石流的运动与冲击特性,为进一步实施不同浆体粘度、不同固相比、不同颗粒粒径耦合作用下泥石流冲击特性研究提供参考与借鉴。
1 实验模型设计
1.1 实验模型
本实验选取西昌-木里干线公路雅砻江河谷中游的平川泥石流为原型(图1),考虑模型尺寸相似、地形相似,在重庆交通大学泥石流动力模型实验场修筑沟谷泥石流实验模型。泥石流主沟槽长15.0 m,平均沟槽宽度0.5 m,平均深度0.6 m,高差3.6 m;设置两个弯道,第一弯道上游坡度27°,下游坡度10°。沟槽顶端为水源箱,1.0 m(长)×1.0 m(宽)×1.5 m(高),储水量1.5 m3;水源箱出口放置抽板式碎石漏斗。泥石流沟口安置动态应力传感器,实验模型设计平面图及纵面图见图2与图3,修筑完成后的实验模型见图4。

图1 平川泥石流沟平面图Fig.1 Plane figure of Pingchuan debris flow
1.2 实验工况
本文进行不同泥石流浆体粘度下的泥石流运动与冲击特性实验,浆体粘度分为5组(表1)。
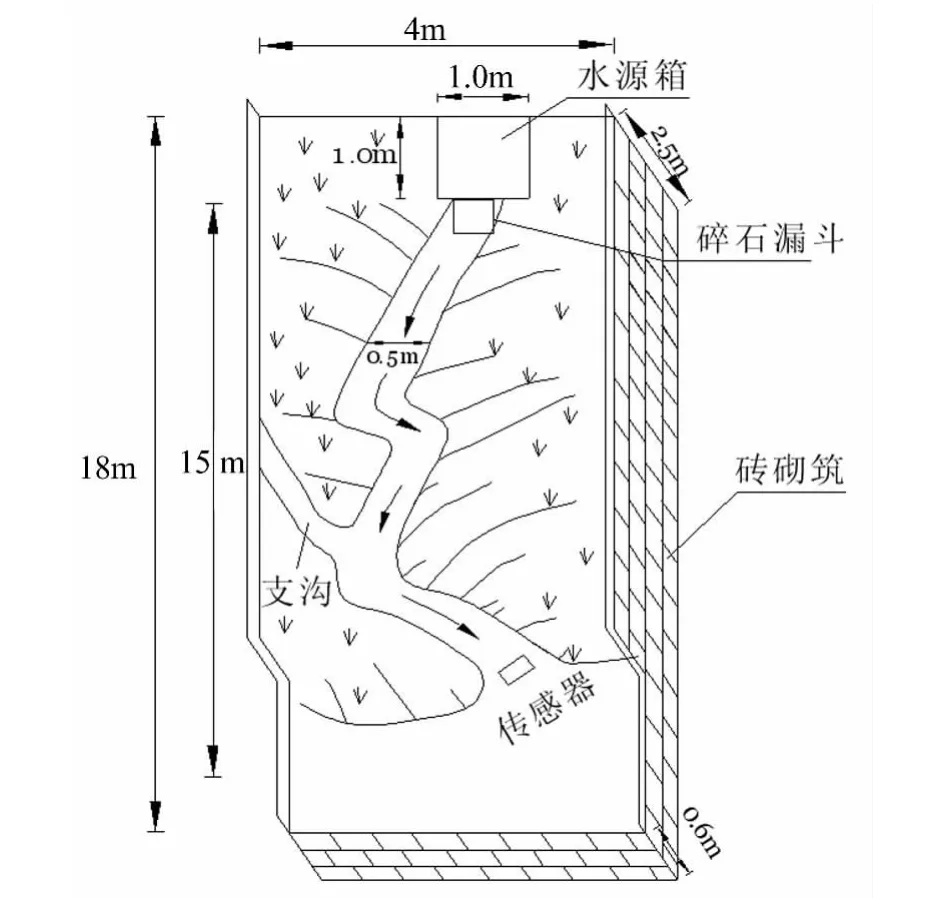
图2 实验模型设计平面图Fig.2 Designing plane figure of the testing model
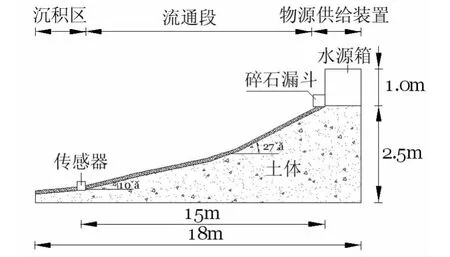
图3 实验模型设计纵剖面Fig.3 Longitudinal section of the testing model

图4 泥石流运动与冲击特性实验模型Fig.4 The testing model of the debris flow impacting test

表1 实验工况Tab.1 Working conditions of the test
泥石流浆体粘度采用熟胶粉、淀粉醚与水配制而成,采用NDJ-1旋转粘度计测定配制后的泥石流浆体(图5),使其达到预期粘度要求,浆体材料配置结果见表2。

图5 旋转粘度计测量泥石流浆体粘度Fig.5 Measuring the slurry viscosity with rotaryviscometer
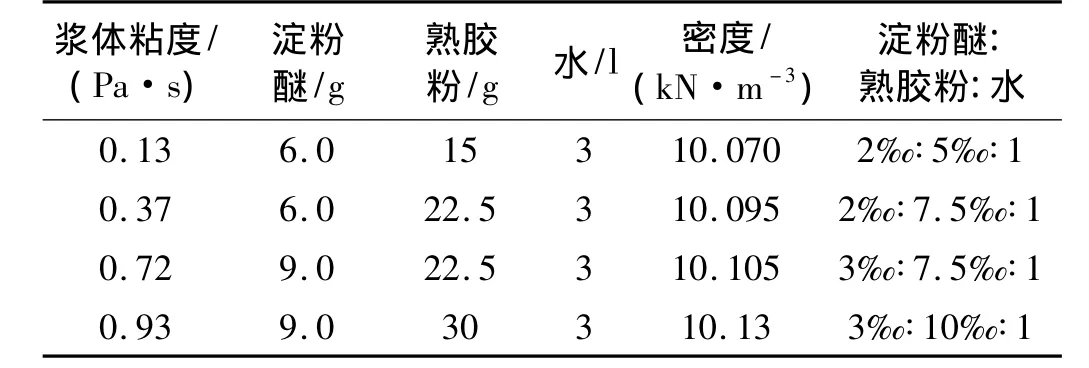
表2 泥石流浆体粘度配置Tab.2 The collocation of the slurry viscosity
1.3 实验过程过程
泥石流沟口安置HS200型动态应力传感器,精度为5‰;动态信号测试系统采用江苏东华测试技术有限公司生产的DH5922动态信号测试系统,采样频率设定为1 000 Hz;高精度摄像仪型号为Fastcam-ultimal024,测试精度选用400 fpt。
实验过程包括两方面:
(1)将蓄水池蓄满,逐次加入相应配比的淀粉醚与熟胶粉,搅拌均匀直至反应完全,用粘度计测定冲击前泥石流浆体粘度(与实验室内预配粘度吻合)。
(2)打开水源箱阀门,高速摄像机连续记录泥石流运动过程,传感器接收泥石流冲击,将冲击荷载信号传至动态信号测试系统,连续记录泥石流冲击荷载变化过程(图6)。

图6 泥石流冲击模型实验现场图Fig.6 Testing field of theimpacting test of debris flow
2 实验结果分析
2.1 冲击荷载谱
根据动态信号测试系统采集到的5组浆体粘度泥石流冲击荷载数据达203 380个,截取传感器感受到不为零冲击力的初始点与恢复零点之间的冲击荷载。
DH5922动态信号测试分析系统所采集的数据在记录有效冲击荷载信号的同时也记录了各种各样的的噪音,即采集到的信号Xn由噪声en与真实的信号fn组成,即

因此,为获取逼近真实的信号,必须进行降噪处理。
小波降噪在信号降噪中的应用十分广泛,其基本思想是:对含噪信号进行小波分解,在提取有效信号的小波系数时去除噪声的小波系数,最后重构信号以达到目的。其核心是判断信号与噪声的小波系数,基于不同的准则即可得到不同的消噪算法,其中Daubechie(dbN)小波具有正交性,对于随机性较强的泥石流冲击脉动荷载信号的重构可获得较好的平滑效果,因此,本实验采用db8小波按照信号小波分解→小波分解高频系数的阈值量化→小波重构的步骤进行8层尺度的软阈值冲击信号的降噪处理。得到降噪后不同浆体粘度泥浆冲击荷载谱图如图7所示。
根据以上冲击荷载曲线可以看出,清水流与浆体粘度为0.13 Pa·s时的冲击荷载曲线呈整体脉动性,仅在初始接收到冲击时,由于龙头压胀作用而冲击力急剧增长,呈现明显的的阵动,其中浆体粘度为0.13 Pa·s的冲击曲线在整体脉动的趋势下,细节部分呈现出阵动性;浆体粘度0.37 Pa·s时,冲击曲线仍整体呈脉动曲线,但在20~25 s处出现一个明显的阵动;浆体粘度0.72 Pa·s时,冲击曲线在 0 ~5 s,5 ~15 s,20 ~25 s都有明显阵动,是一个明显的阵动曲线;在浆体粘度为0.93 Pa·s时,冲击曲线细节呈现为一阵动曲线,但是整体曲线在前0~5 s呈阵动性,5~20 s呈脉冲性,20 s过后呈较光滑的波动性。可见,随着浆体粘度的增加,冲击曲线特征从脉动曲线逐渐变化为阵动曲线,在粘度达到0.93 Pa·s后,冲击曲线逐渐呈波动性。
2.2 不同浆体粘度泥石流冲击荷载概率分布特征
冲击荷载信号的概率分布函数是指冲击荷载信号以N个样本函数的集合X={x(n)},其中在t1时刻,有N1个样本函数的函数值不超过指定值x,则它的概率分布函数的估计为:
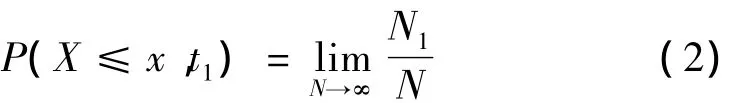
概率密度函数即为概率分布函数对变量x的一阶导数,表示一冲击荷载信号的幅值落在某一范围内的概率,其概率密度函数的估计为:

式中:Δx是以x为中心的窄区间;Nx为{xn}数组中数值落在x±Δx/2范围中的数据个数;N为总的数据个数。
将实验获得的数据进行概率统计,得到5种浆体粘度泥石流的冲击信号均值和标准差对比见表3及图8及图9,各组概率密度分布见图10。

图7 不同工况下泥石流冲击荷载谱图Fig.7 Impacting load Spectrum of different conditions
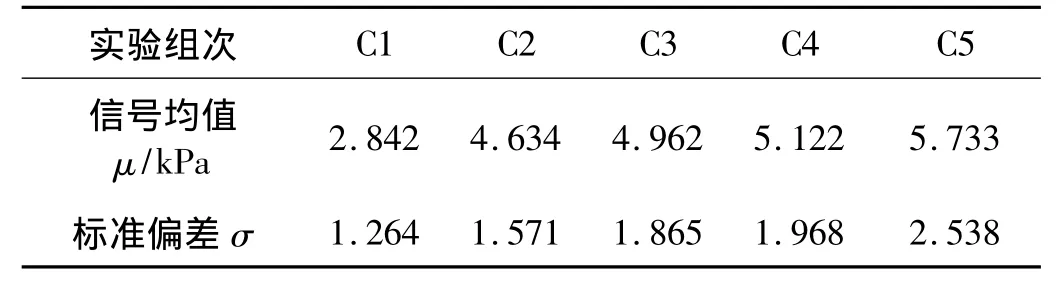
表3 不同浆体粘度泥石流冲击荷载均值及标准差Tab.3 The meen value and standard deviation of debris flow's impacting load under different slurry viscosities

图8 各组泥石流冲击荷载均值Fig.8 Mean impacting loadfor each debris flow condition

图9 各组泥石流冲击荷载标准差Fig.9 Standard deviation of each debris flow’simpacting load
根据以上数据可见:随着浆体粘度的增大,泥石流的冲击力与标准差均呈非线性增大,泥石流冲击力概率密度由近似正态分布逐渐偏离,冲击力从单峰(C1和C2工况),变为双峰(C3和C4工况),甚至变为多峰(C5工况)。
2.3 不同浆体粘度泥石流冲击荷载时频特征
根据信号学知识,db小波具有阶数越高规则性越高的特性,为了得到不同浆体粘度泥石流的时频及能量特征,本实验采用db8小波对信号进行8层一维多尺度分解,以便研究激振信号各频带的能量分布规律。则冲击荷载数据S的分解具有如下关系:

式中:a8为第8层分解后的低频信号,d1,d2……d7分别为第1,2,……,第7层分解后的高频信号。
以浆体粘度为0.37 Pa·s的C3组实验数据为例,降噪后的数据进行一维多尺度小波离散分解,并对分解后的激振信号进行重构,得到对应分解后的9个频谱图见图11。
由图11可得C3工况泥石流冲击信号一维多尺度分解的细节信息,其中d1,d2,…d8是细节系数中高频率部分,d1是细节系数中频率最低部分,振幅最低,所含能量也较小。为获取对应频带的频谱图,选取C3工况冲击信号小波分解后的重构波形图进行快速傅里叶变换(FFT),其频谱图如图12所示。

图10 各组泥石流冲击荷载概率密度Fig.10 Probability density of each work condition

图11 C3工况冲击信号分解后的重构信息Fig.11 Reconstructed information of impaction signal of C3

图12 C3工况冲击信号分解后的频谱图Fig.12 Analytical spectrum of C3 impacting load
其频谱图所对应的9个频率带分别是,频段1(a8)对应0 ~1.958 Hz;频段2(d8)对应1.958 ~3.906 Hz;频段3(d7)对应 3.906 ~7.812 Hz;频段 4(d6)对应7.812~15.625 Hz;频段 5(d5)对应 15.625 ~ 31.25 Hz;频段6(d4)对应31.25 ~62.5 Hz;频段7(d3)对应62.5~125 Hz;频段 8(d2)对应 125~250 Hz;频段9(d1)对应250~500 Hz。
2.4 冲击荷载信号各频带能量分布规律
泥石流冲击信号属于典型的非平稳信号,采用传统的傅里叶变换直接进行分析,其结果有可能掩盖冲击信号的真实频率特征。将傅里叶变换和小波分析理论结合起来,采用小波包分解把冲击信号分解为不同频带,然后通过各频带的能量分析,就能获得较准确的频率特性。
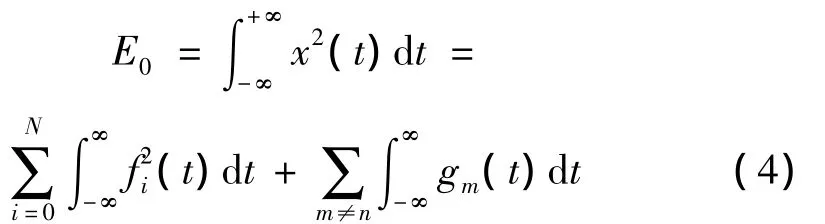
式中:E0为冲击信号总能量;x(t)表示原始信号;f(t)表示为经分解后得到的低频信号;g(t)表示经分解后得到的高频信号。
由此可得到不同频段上冲击信号的相对能量分布为:

式中:E为冲击信号的相对能量百分比;Ei为各频带冲击信号能量。
由上式通过MATLAB编程对冲击荷载信号进行FFT变换,可以得到C3工况冲击信号db8(8层)小波包分解后的9个频带的能量占总能量的百分比(表4)。

表4 冲击信号各层分解信号的波峰值及能量百分比Tab.4 The wave-crest value and energy percentage of analytical impacting load
从表4数据可以看出,C3工况泥石流冲击信号99%的能量都聚集在低频部分,随后在高频部分能量分布急速衰减。各频带的主振频率包含了该频带冲击信号的主要特征和大部分能量。由此可见,该组泥石流冲击信号的能量分布主要集中在低频段(0~1.958 Hz)内。
根据以上研究方法,对 C1、C2、C3、C4、C5 组泥石流的冲击信号通过小波分解,重构,FFT变换进行频谱特征及能量分布特性研究,得到结果如图13和图14所示。

图13 低频段泥石流冲击能量及能量百分比Fig.13 Impaction energy and energy percentage of low frequency debris flow(1-C1;2-C2;3-C3;4-C4;5-C5)
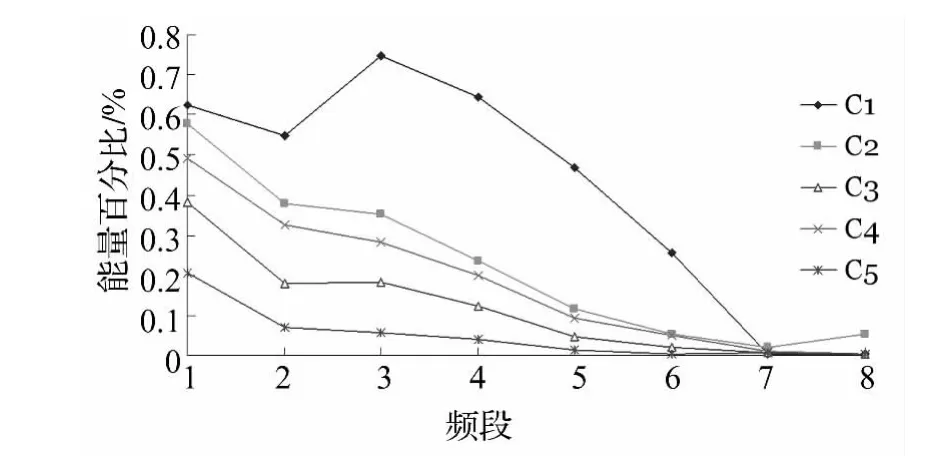
图14 高频段泥石流冲击能量及能量百分比Fig.14 Impaction energy and energy percentage of high frequency debris flow(1-d8;2-d7;3-d6;4-d5;5-d4;6-d3;7-d2;8-d1)
根据图13所示,随着泥石流浆体粘度的增加,其积聚在低频(0~1.958 Hz)的冲击能量越大,且其所占能量百分比也逐渐增大(96.7% ~99.6%),说明浆体粘度越大,其冲击能量越多的积蓄在低频阶段。由图14可知,泥石流冲击能量在高频部分(1.958 Hz~500 Hz)的能量百分比在5%以下,且随着频段越高,能量百分比越低(仅在d6频段比d5频段能量百分比有所增加),且随着泥石流浆体粘度的增大,其在高频频段的能量百分比越低。
3 结论
以平川泥石流沟为原型自行研制粘性泥石流运动与冲击特性实验模型,实施了C1(粘度0 Pa·s)、C2(粘度 0.13 Pa·s)、C3(粘度 0.37 Pa·s)、C4(粘度0.72 Pa·s)、C5(粘度0.93 Pa·s)五种工况的泥石流浆体冲击实验,获取了203 380多个测试数据,所得初步结论如下:
(1)泥石流浆体粘度越大,冲击荷载越大,五种粘度泥石流浆体冲击信号均值分别为2.842 kPa、4.634 kPa、4.962 kPa、5.122 kPa、5.733 kPa。
(2)运用db8小波基对实验结果进行8层小波分解,得到泥石流冲击荷载信号频率范围分别为0~1.958 Hz、1.958 ~3.906 Hz、3.906 ~7.812 Hz、7.812 ~15.625 Hz、15.625 ~31.25 Hz、31.25 ~62.5 Hz、62.5 ~125 Hz、125 ~250 Hz、250 ~500 Hz九个频带。
(3)获得了五组工况下不同频段的泥石流冲击信号能量分布,得到泥石流95%以上的冲击能量分布在小于1.958 Hz的低频部分。
(4)泥石流冲击能量百分比从低频至高频呈迅速衰减分布趋势,泥石流粘度越高,衰减速度越快。
[1] Hu K,Wei F,Li Y.Real- time measurement and preliminary analysis of debris-flow impact force at jiangjia ravine,China[J].Earth Surf Process Landf,2011,36:1268-1278.
[2]崔 鹏.我国泥石流防治进展[J].中国水土保持科学,2009,7(5):7 -13.CUI Peng.Advances in debris flow prevention in China[J].Science of Soil and Water Conservation,2009,7(5):7 -13.
[3]费祥俊.粘性泥石流的输沙浓度与运动速度[J].水利学报,2003(2):15-18.FEI Xiang-jun.Vdodty and solid transportation concentration of VISCOUS debris flow[J]. Journal of Hydraulic Engineering,2003(2):15 -18.
[4]陈洪凯,唐红梅,陈野鹰,等.泥石流固液分相流速计算方法研究[J].应用数学和力学,2006,27(3):357 -364.CHEN Hong-kai,TANG Hong-mei,CHEN Ye-ying,et al.Research on method to calculate velocities of solid phase and liquid phase in debris flow[J].Applied Mathematics and Mechanics,2006,27(3):357 -364.
[5] Valentino R,Barla G,Montrasio L.Experimental analysis and micromechanical modeling of dry granular flow and impacts in laboratory flume tests[J].Rock Mechanics and Rock Engineering,2008,41(1):153 -177
[6] Yang H J,Wei F G,Hu K H,et al.Measuring the internal velocity of debris flows using impact pressure detecting in the flume experiment[J]. Journal of Mountain Science,2011(8):109-116.
[7] Wang Y Y,Tan R Z,Hu K H,et al.Experimental study on the viscoelastic behaviors of debris flow slurry[J].Journal of Mountain Science,2012(9):501 -510.
[8] Scheidl C,Chiari M,Kaitna R,et al.Analysing debris-flow impact models,based on a small scale modelling approach[J].Surv Geophys,2012(12):199 -204.
[9]Bugnion L,McArdell B W,Bartelt P,et al.Measurements of hillslope debris flow impact pressure on obstacles[J].Landslides,2012,9:179 -187.
[10]吴积善,田连权,康志成,等.泥石流及其综合治理[M].北京:科学出版社,1993.
[11]张 宇,韦方强,王 青.基于动量守恒的粘性泥石流冲击力计算[J].泥沙研究,2006(3):23-26.ZHANG Yu,WEI Fang - qiang,WANG Qing.IImpact force calculation of viscous debris flow[J].Journal of Sediment Reasearch,2006(3):23-26.
[12]陈洪凯,唐红梅.泥石流两相冲击力及冲击时间计算方法[J].中国公路学报,2006,19(3):19 -23.CHEN Hong-kai,TANG Hong-mei. Method to calculate impact force and impact time of two-phase debris flow[J].China Journal of Highway and Transport,2006,19(3):19-23.
[13]陈洪凯,唐红梅,鲜学福.沟谷泥石流运动过程模型试验[J].自然灾害学报,2009,18(6):160 -165.CHEN Hong-kai,TANG Hong-mei,XIAN Xue-fu.Model test of valley-shaped debris flow motion[J].Journal of Natural Disasters,2009,18(6):160 -165.
[14]陈洪凯,唐红梅,鲜学福,等.泥石流冲击特性模型试验[J].重庆大学学报,2010,33(5):114 -119.CHEN Hong-kai,TANG Hong-mei,XIAN Xue-fu,et al.Experimental model of debris flow impact features[J].Journal of Chongqing University,2010,33(5):114 -119.
[15]陈洪凯,唐红梅,鲜学福,等.泥石流冲击脉动荷载概率分布特征[J].振动与冲击,2010,29(8):124 -127.CHEN Hong-kai, TANG Hong-mei,XIAN Xue-fu,et al.Probability distribution features of fluctuating impact force of debris flow[J].Journal of Vibration and Shock,2010,29(8):124-127.
[16]陈洪凯;鲜学福;唐红梅,等.水石流冲击信号能量分布试验研究[J].振动与冲击,2012,31(14):56 -59.CHEN Hong-kai,XIAN Xue-fu,TANG Hong-mei,et al.Energy distribution in spectrum of shock signal for nonviscous debris flow[J].Journal of Vibration and Shock,2012,31(14):56-59.
