串联隔震体系水平刚度的参数研究

杜永峰，吴忠铁，范萍萍

同理，可以得到钢筋混凝土柱的水平变形和转角方程:

随着隔震结构的迅速推广和建设，为了满足工程实际的要求，出现了大量的带有地下室的串联隔震结构，其特点是把叠层橡胶支座和钢筋混凝土柱组成的串联隔震体系作为隔震结构的隔震层，其力学性能变化值得关注，特别是隔震层刚度的变化。国内外对于叠层橡胶支座已经进行了深入的研究，并得到很多成果。40年代Haringx［1］建立隔震装置在小变形状态下基本模型。Gent［2］最早基于Haringx理论研究了叠层橡胶支座的力学性能。Koh和Kelly等［3～7］提出了一种线性形式的非线性模型，探讨了橡胶支座的轴向载荷对水平刚度的影响，进而分析了叠层橡胶支座的拉伸和压缩屈曲、稳定性以及后屈曲行为。在此基础上Nagarajaiah等［8］提出了改进的非线性解析模型，得到的屈曲荷载和水平刚度更加精确。Iizuka［9］提出了叠层橡胶支座稳定分析的宏观力学模型。国内的周福霖、刘文光、张敏政、杨巧荣等［10～12］率先针对叠层橡胶支座的竖向刚度、水平刚度、回转刚度以及稳定性等性能进行了理论分析和试验研究;而对于串联隔震体系的研究相对较少，周锡元等［13］在Harings和Gent研究基础上建立了柱串联隔震系统的分析模型，推导出柱串联隔震系统的水平刚度计算公式及临界荷载求解公式。杜永峰等［14～16］采用矩阵传递法对于串联隔震体系进了理论分析和相关的缩尺实验。本文在前人研究的基础上，根据串联隔震体系自身的特点，采用直接积分的方法建立了叠层橡胶支座的变形方程，根据构件对称的特点，直接给出钢筋混凝土柱的变形方程，结合整体力的平衡方程和交接面的变形协调方程，求解出了各构件的水平刚度和整体刚度方程，并进行了典型参数研究。

1 理论分析

串联隔震体系主要由叠层橡胶支座和钢筋混凝土柱两部分组成，如图1(a)所示。图中给出了各部分的局部坐标系，计算分析时均根据自身局部坐标处理。其中，叠层橡胶支座的高度为h，变形为YR(h)，抗弯刚度为ERIR，抗剪刚度为GRAR，钢筋混凝土柱的高度为H，变形为YC(H)，抗弯刚度为ECIC，抗剪刚度为GCAC，截面形状系数μR和μC。可得整体变形方程Y:

当考虑弯曲变形YRM(XR)和剪切变形YRQ(XR)时，叠层橡胶支座的水平变形方程YR(XR):

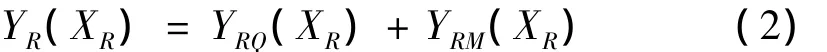
对式(2)求导可得:

其中:γR(XR)为剪力产生的剪切角，θR(XR)为弯矩产生的截面转角，YR(XR)＇截面实际转角，如图1(c)。

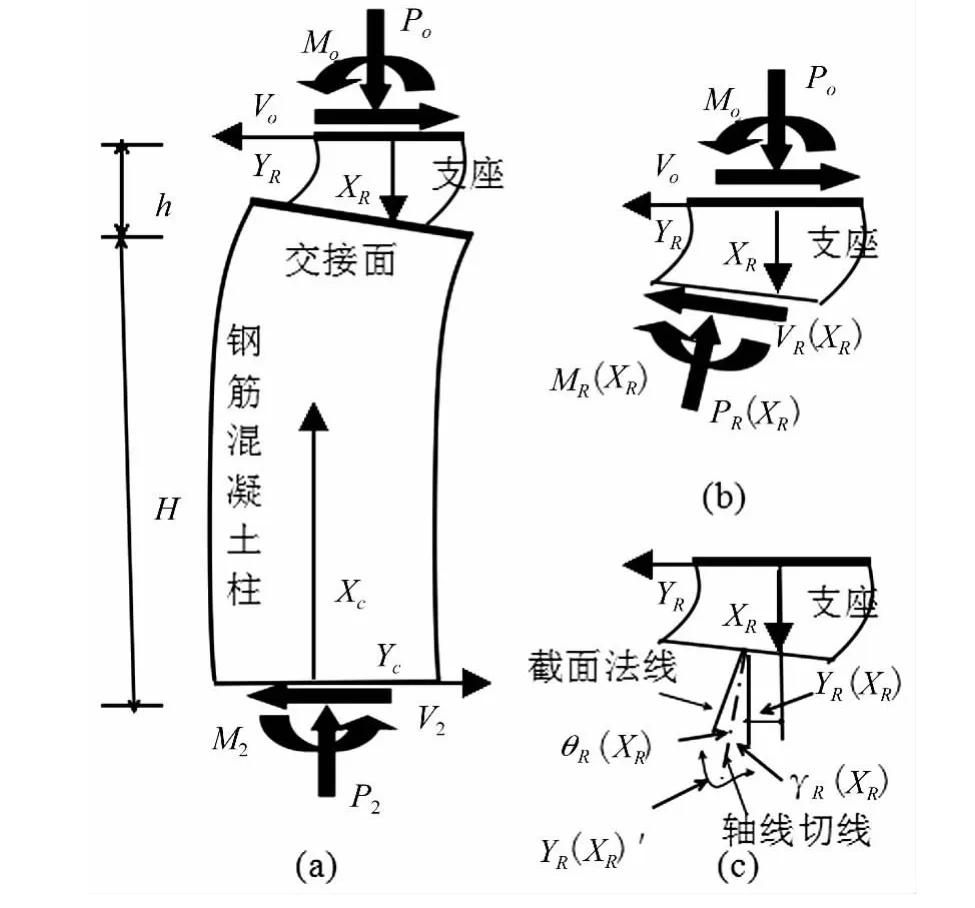
图1 基本模型Fig.1 Basic model

由图1(b)叠层橡胶支座任意截面本构关系方程:

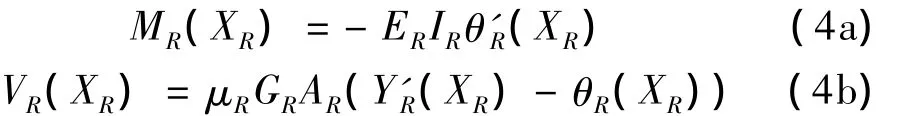
其力的平衡方程:

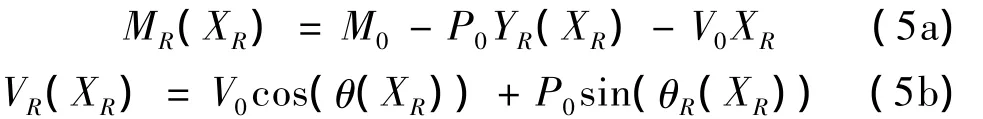
当θ(x)→0时，式(5b)可变为:

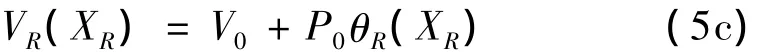
由方程(4)和(5)联立可得到方程(6):

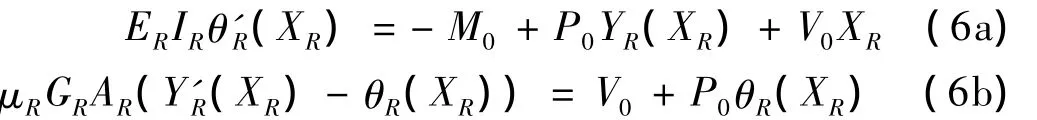
将(6b)变化可得到(7)式:

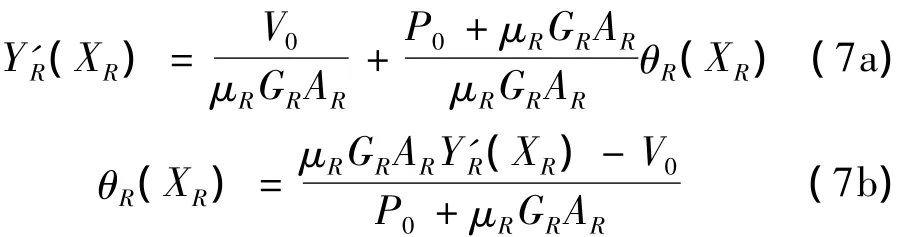
将(7b)求导代入(6a)式中可得到:

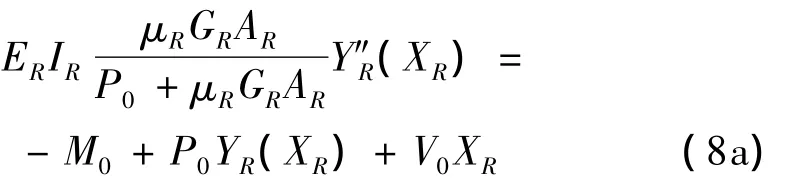
对(6a)求导，并将(7a)代入得:

方程(8)的通解为:

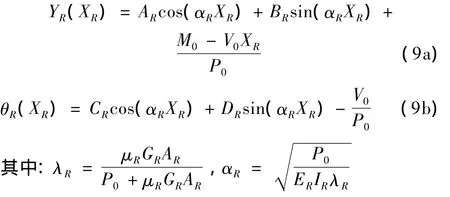
边界条件:

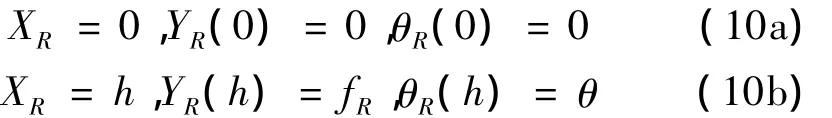
由边界条件可得:

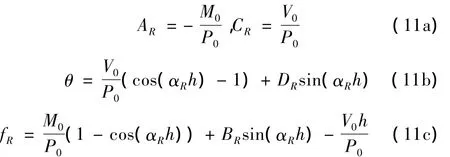
将方程(9a)求导及(9b)代入(7a)可得:

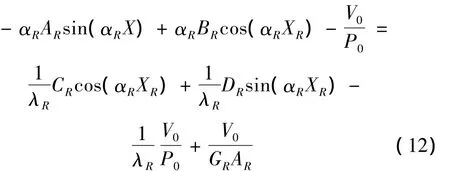
由相同项系数相同，可得到BR和DR:

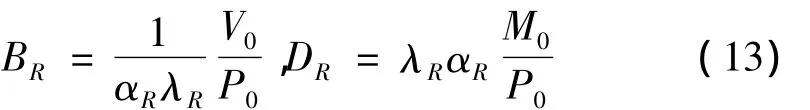
叠层橡胶支座的位移和转角方程:

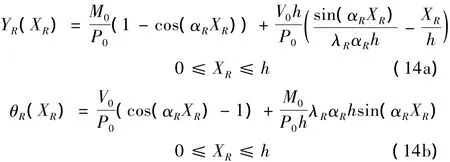
同理，可以得到钢筋混凝土柱的水平变形和转角方程:

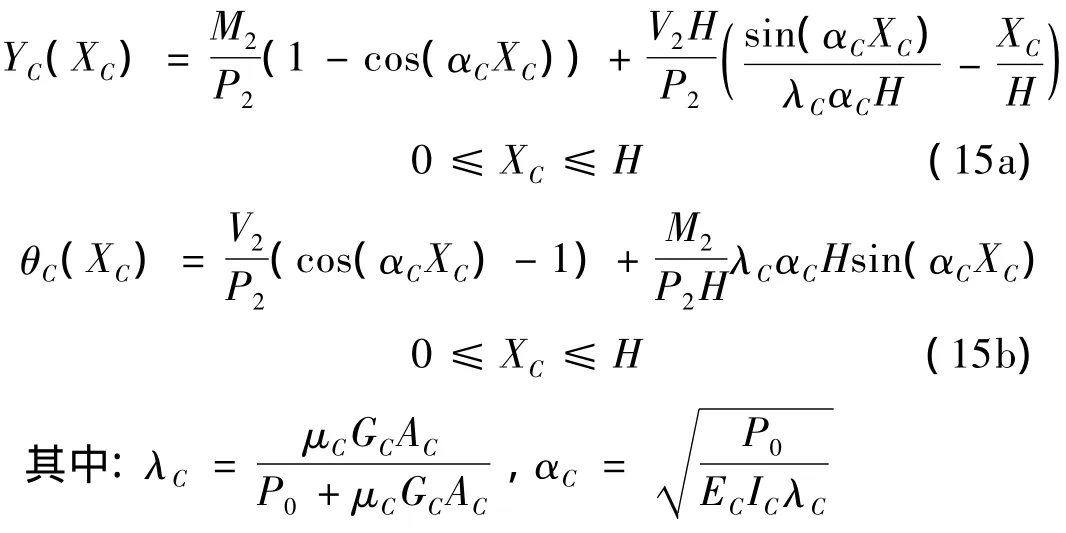
由整体受力平衡和交接面处变形协调条件:

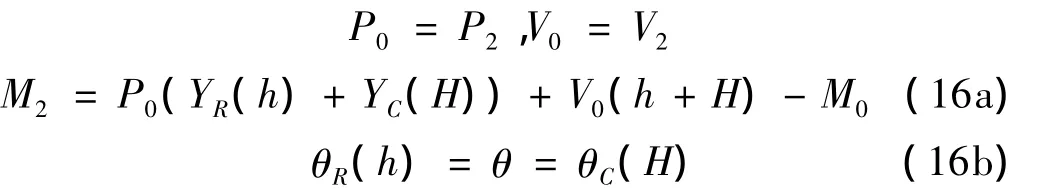
解方程(16)可得:

其中:

当KC(P)≈∞时，可认为叠层橡胶支座底部固结，则式(22)为0。

综合上述方程，为了方便串计算联隔震体系整体刚度Knon(P)，提出一种组合形式的串联隔震体系刚度简化方程:

上式包括两部分:第一部分KSRnon为单个叠层橡胶支座的影响部分，两者组合构成整体刚度的简化方程。

2 参数设定与分析

上述理论方程中含 εR，εC，λR，λC四个参数，参数中叠层橡胶支座和钢筋混凝土的材料属性可根据文献［17］和《混凝土结构设计规范》(GB50010－2010)来确定。为了降低参数之间的关联性，并侧重于分析轴力和高度比对刚度的影响，将其分离成五个无量纲参数

将文献［6］中给出刚度近似公式(30)根据参数设定的不同，可得到:

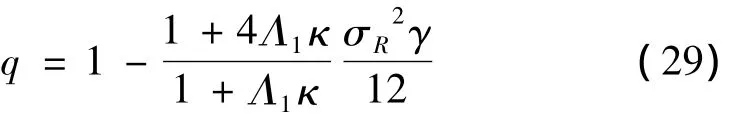
为了研究串联隔震体系刚度变化的特点，对于给定的 σR，κ，γ，Λ1，Λ2进行定量处理。根据文献［17］附录提供的叠层橡胶支座的参数，结合混凝土材料的特性，考虑施工和安装的要求，保持混凝土柱方形截面尺寸比叠层橡胶支座的直径DR大0.1 m，计算得到参数γ，Λ1，Λ2与直径DR和橡胶剪切模量Gr的变化关系曲线，如图2所示，γ随着 DR的增大而降低，其值在［0.00 1，0.00 4］区间变化，Λ1和 Λ2随着 DR的增大而增大，其值分别在［0.005，0.025］和［0.000 035，0.000 07］区间变化，为了保证所确定参数在一定范围内的合理性，γ，Λ1，Λ2均取变化区间的中间值，设定 γ =0.002 5，Λ1=0.015，Λ2=0.000 06。进而可以分析 σR和κ分别与叠层胶支座无量纲刚度KRnon、柱无量纲刚度KCnon、整体无量纲刚度Knon及单独叠层橡胶支座无量纲刚度KSRnon的变化关系，如图3～9所示。

图3、4 分别给出了 κ =4、10、16 和 σR=3、9、15 情况下，KRnon和 Knon及文献［5］和［6］公式随着参数 σR和κ的变化情况，表明在σR、κ一定的情况下，随着σR和κ增大刚度降低的速度加快，KRnon和Knon及文献［6］公式与文献［5］单独叠层橡胶支座刚度公式相比降低较为明显，变化趋势一致，但数值存在一定差别;随着参数的不同，整体刚度Knon与单独叠层橡胶支座的刚度KSRnon差别较大，表明钢筋混凝土柱对叠层橡胶支座的刚度有较大影响。从图5中可以发现当参数κ≤10，σR≤10时，即黑线标定范围内，整体刚度和叠层橡胶支座的刚度差值很小，均在3%以内，满足工程需求，可直接采用叠层橡胶支座的刚度KSRnon来代替串联体系的刚度Knon进行设计和计算。

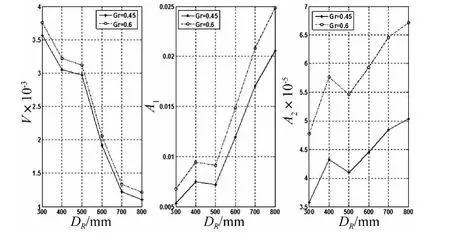
图2 参数γ、Λ1和Λ2与叠层橡胶支座直径的关系Fig.2 The relation between parametersγ and Λ1 and Λ2 and diameter of the laminated rubber bearing

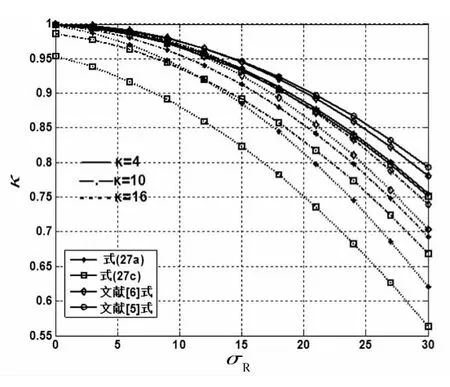
图3 无量纲刚度K与σR的变化关系Fig.3 The relation between non-dimensional horizontal stiffness K andσR

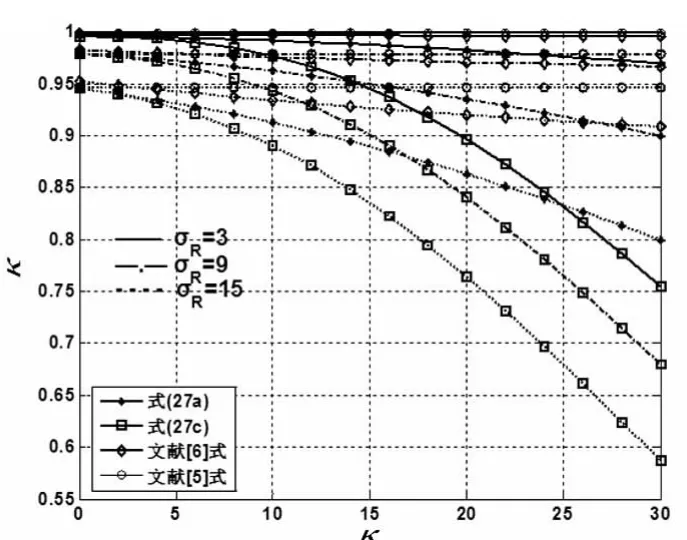
图4 无量纲刚度K与κ的变化关系Fig.4 The relation of non-dimensional horizontal stiffness K andκ

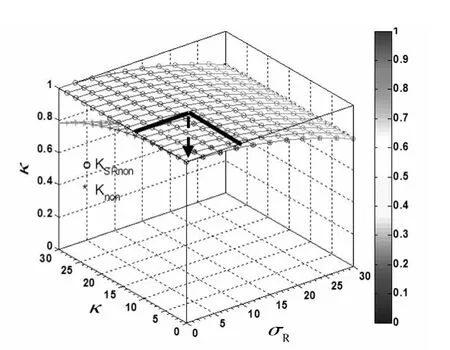
图5 无量纲刚度K与参数σR和κ的三维图Fig.5 The three dimensional diagram of non-dimensional horizontal stiffness K and parametersσR andκ

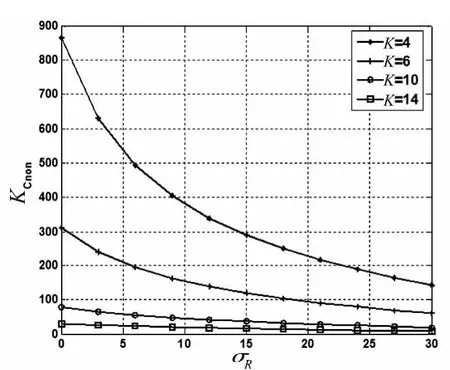
图6 无量纲刚度KCnon与σR的变化关系Fig.6 The relation of non-dimensional Horizontal stiffness KCnon andσR

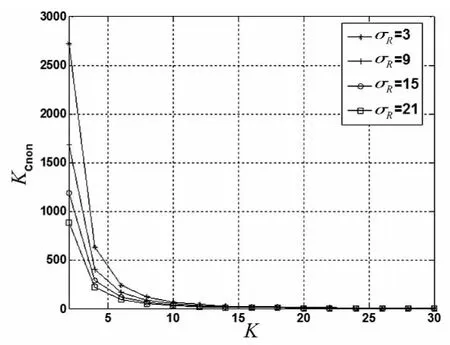
图7 无量纲刚度KCnon与κ的变化关系Fig.7 The relation of non-dimensional horizontal stiffness KCnon andκ

图8 整体无量纲刚度K与σR的变化关系Fig.8 The relation between non-dimensional horizontal stiffness K andκ

图6 、7表明在σR和κ一定情况下，钢筋混凝土柱随着σR和κ的增大刚度降低的速度加快，影响较为明显，表明叠层橡胶支座对钢筋混凝土柱的刚度有较大影响。

图8、9为整体刚度Knon和整体简化刚度KSnon与参数σR、κ变化关系，简化方程与整体刚度方程都存在一定误差，但简化方程相对较小，图7中在σR=20时差值在0.1以内，在κ=4时随着σR有较好的一致性，图8中在κ=20时差值在0.1以内，σR=9时随着κ变化有较好的一致性。

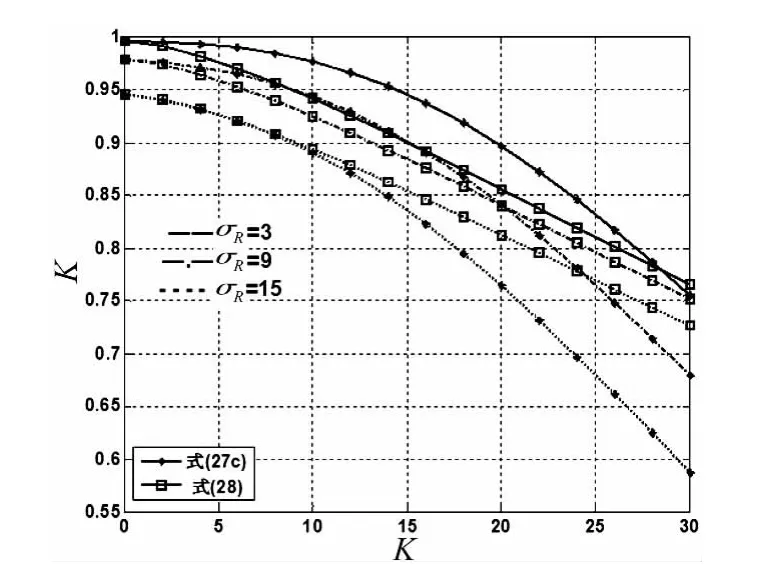
图9 整体无量纲刚度K与κ的变化关系Fig.9 The relation between non-dimensional horizontal stiffness K andκ

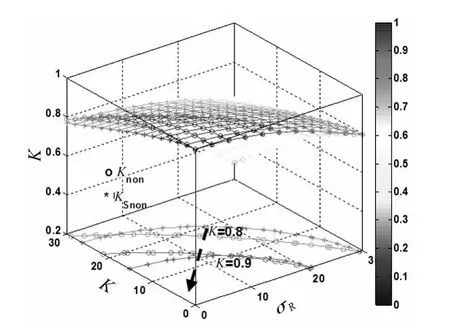
图10 无量纲刚度K与参数σR和κ的三维图Fig.10 The three dimensional diagram of non-dimensional horizontal stiffness K and parametersσR andκ

从图10可以看出在本文给定参数下，简化方程计算的整体刚度KSnon和精确方程计算的整体刚度Knon随参数σR和κ两者变化趋势基本一致。底面的曲线为刚度等值线，在所给定的红色区域内有误差较小，在5%以内，满足工程要求。

3 结论

本文对串联隔震体系的刚度方程进行了理论推导，采用典型参数对串联隔震体系中叠层橡胶支座刚度、钢筋混凝土柱刚度和整体刚度及单独叠层橡胶支座的水平刚度进行了对比分析，得到以下主要结论:

(1)在串联隔震体系中，叠层橡胶支座和钢筋混凝土柱的刚度相互影响，随着参数的变化影响不同。

(2)在串联隔震体系中，随着参数的变化，串联隔震体系刚度Knon与单独叠层橡胶支座刚度KSRnon存在差距较大，在隔震设计时，应该考虑整体刚度;同时可通过调整钢筋混凝柱的参数从而改变整体刚度，当σR≤10，κ≤10时与单独叠层橡胶支座刚度差别很小，可以采用单独叠层橡胶支座刚度KSRnon替代。

(3)在本文给定范围内，整体简化刚度KSnon和整体精确刚度Knon误差较小，为整体刚度提供了一种简便计算方法。

［1］Haringx J A.On highly compressible helical springs and rubber rods and their application for vibration－free mountings［J］.I.Philips Res.Rep.，1948，3:401 － 449.

［2］ Gent A N.Elastic stability of rubber compression springs［J］.Journal of Engineering Mechanics，1964，6(4):318 －326.

［3］Koh C G，Kelly J M.A simple mechanical model for electrometric bearings used in base isolation［J］.Journal of Engineering Mechanics，1988，30(12):933 －943.

［4］Imbimbo M，Kelly J M.Stability of isolators at large horizontal displacements ［J］.Earthquake Spectra，1997，13(3):415－430.

［5］Kelly JM.Tension buckling in multilayer elastomeric isolation bearings ［J］.Journal of Engineering Mechanics，2003，129(12):1363－1368.

［6］Imbinmo M，Kelly J M.Stability aspects of elastomeric bearings［J］.Earthquake Spectra，1997，13(3):431 －449.

［7］Kelly J M，Marsico M R.Stability and post－buckling behavior in nonbolted elastomeric isolators［J］.Seism.Isolation Protect.Syst，2010，1(1):41 －54.

［8］Nagarajaiah S，Ferrell K.Stability of electrometric seismic isolation bearings［J］.Journal of Structural Engineering，1999，125(9):946 －954.

［9］Iizuka M. A macroscopic model for predicting large deformation behavior of laminated rubber bearing ［J］.Engineering Structures，2000，22(4):323 －334.

［10］刘文光，周福霖，庄学真.柱端隔震夹层橡胶垫力学性能试验研究［J］.地震工程与工程振动，1999，19(3):121－126 LIU Wen-guang， ZHOU Fu-lin， ZHUANG Xue-zhen.Mechanic characteristics of rubber bearings in column top isolation system ［J］. Earthquake Engineering and Engineering Vibration，1999，19(3):121－126.

［11］张敏政，孟庆利，裴 强.叠层橡胶隔震支座的动态稳定性和力学特性研究［J］.地震工程与工程振动，2002，22(5):87－91.ZHANG Min-zheng，MENG Qing-li，PEI Qiang. Dynamic stability and mechanical behaviors of laminated rubber bearings［J］.Earthquake Engineering and Engineering Vibration，2002，22(5):87－91.

［12］杨巧荣，庄学真，刘文光，等.夹层橡胶隔震支座全刚性性能、回转刚性及高压缩应力性能试验研究［J］.地震工程与工程振动，2000，20(4):118 －125.YANG Qiao-rong，ZHUANG Xue-zhen，LIU Wen-guang，et al.Entire-stiffness，rotational stiffness and compressive stress of rubber properties of high bearings［J］.Earthquake Engineering and Engineering Vibration，2002，20(4):118－125.

［13］周锡元，韩 淼.橡胶支座与R/C柱串联隔震系统水平刚度系数［J］.振动工程学报，1999，12(2):159－165.ZHOU Xi-yuan，HAN Miao.Horizontal rigidity coefficient of the serial system of rubber bearing with column［J］.Journal of Vibration Engineering，1999，12(2):159 －165.

［14］杜永峰，李 慧.叠层橡胶垫与RC柱串联隔震体系的随机屈曲分析［J］.防灾减灾工程学报，2010，30:16 －21.DU Yong-feng，LI Hui.Study on random buckling of the rubber bearing tandem column system［J］.Journal of Disaster Prevention and Mitigation Engineering，2010，30:16－21.

［15］杜永峰，朱前坤，李 慧.串联隔震体系的大变形力学行为分析与试验［J］.振动与冲击，2011，30(11)，236－239.DU Yong-feng，ZHU Qian-kun，LI Hui.Analysis of large deformation behavior of series isolation system and its experimental verification［J］.Journal of Vibration and Shock，2011，30(11):236－239.

［16］杜永峰，朱前坤，李 慧.串联隔震系统水平刚度及对结构地震响应影响［J］.振动与冲击，2011，30(11):21 －24.DU Yong-feng，ZHU Qian-kun，LI Hui.Horizontal stiffness of laminated rubber bearing serially connected with column and its effects on seismic response of isolated structure［J］.Jouranl of Vibration and Shock，2011，30(11):21 －24.

［17］党 育，杜永峰，李 慧.基础隔震结构设计及施工指南［M］.北京:中国水利水电出版社，2007.