基于最小一乘的GA-SVR用电量预测
2013-05-23王晓佳合肥工业大学合肥230009
□章 政 王晓佳 [合肥工业大学 合肥 230009]
引言
近些年来,我国经济高速发展,但这也伴随着能源的快速消耗。同时,随着工业化进程的不断深入和城乡居民生活水平的不断提高,对电力的需求也越发旺盛。因此,对未来用电量的准确预测,将有助于合理地安排生产活动,制定生产计划,维持社会的稳定发展,实现经济效益的快速提升。支持向量机(Support Vector Machine)是由Vapnik等人在1995年提出来的[1],它是基于统计学习理论,采用结构风险最小化的原理,较好地解决了“过学习”的现象,并且具备良好的泛化能力。支持向量回归机(Support vector regression)是将支持向量机应用于回归分析中而形成的。虽然该理论的发展只有不到20年时间,但海内外学者仍然对其展开了广泛地研究。如文献[2]基于支持向量机原理,提出了一个预测系统用以预测输配电线路上的积冰问题;文献[3]通过支持向量机预测了土耳其的用电量情况;文献[4]将免疫优化算法应用于支持向量机的参数寻优中,并建立了优化模型预测台湾各地区的用电量;文献[5]运用蚁群算法优化训练数据,加快了SVM的训练时间;文献[6]应用支持向量回归机原理预测混沌时间序列,实验结果显示SVM方法不仅精度高,而且具有良好的泛化能力;文献[7]运用加权支持向量机原理对不平衡库存问题进行分类研究,取得了较好的结果;文献[8]将主成分分析与支持向量机相结合进行电力预测,加快了学习速度,提高了预测精度。
本研究采用最小一乘原理,通过自适应遗传算法优化支持向量机的模型参数,并且在训练过程中使用了交叉验证的思想,通过江苏省2004年~2009年全社会用电量及宏观经济影响因素月度数据,预测未来的用电量水平。实验结果表明,该模型在拟合度和误差上均优于BP-神经网络模型和传统的SVR模型,并且预测精度也较高。
一、支持向量回归机原理
给定样本空间D=(xi,yi),xi∈Rp,yi∈R,i=1,2,…,n。并且令线性回归函数为

其中:w称为权向量,b称为分类阈值。φ(x) 为一非线性变换,它将数据集x映射到高维的特征空间F中。从而,由结构风险最小化的原则,为求得 f(x),就需要极小化如下泛函:

其中,C是一个正常数,它是模型平坦性和经验误差之间的折中因子,也称为惩罚因子。L(yi,f(xi))为损失函数。一般的,取损失函数为ε不敏感损失函数,即对于i=1,2,…,n,
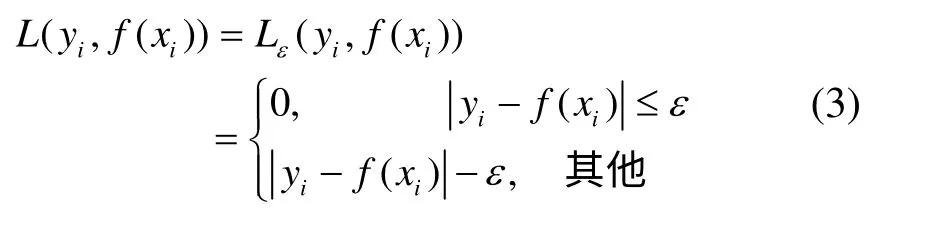
从而问题转化为:
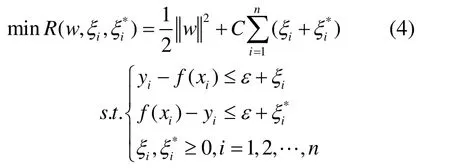
为求解优化问题(4),引入Lagrange 因子αi,βi,μi,υi,i=1,2,…,n,并定义Lagrange函数如下:

对函数L(·)关于变量w,b,ξi,ξi*求偏导,并令其为零,则有
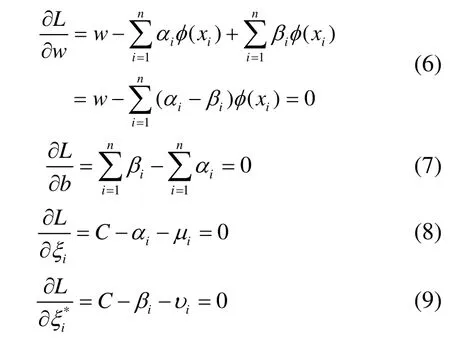
将(6)~(9)式代入(5)式,并将优化问题转化为其对偶问题,则有
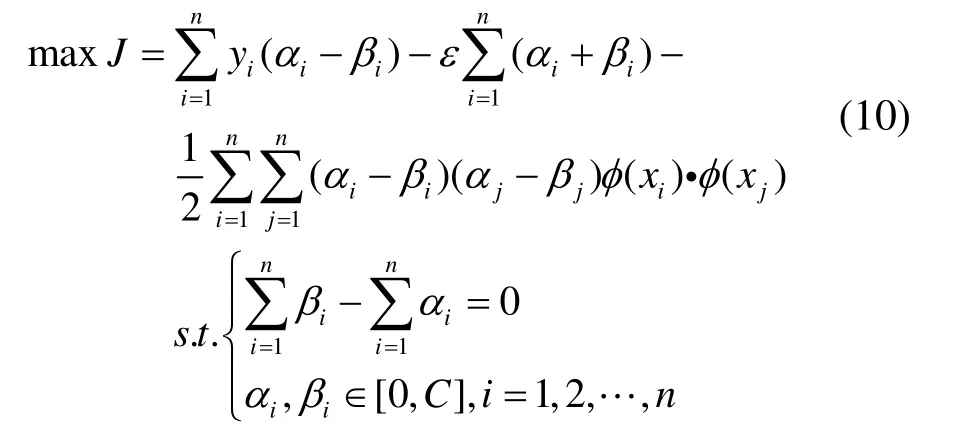
求解二次规划问题(10),有
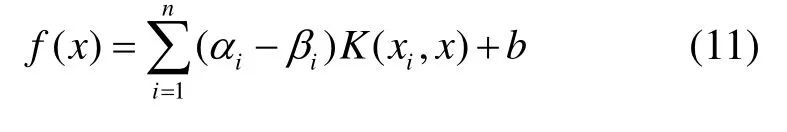
其中:
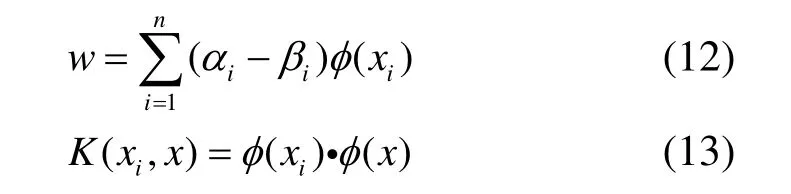
K(xi,x)为核函数,而由于满足Mercer条件的核函数[1],即对应高维空间中的一组点积。从而只需要获得满足该条件的核函数,即可求得回归函数f(x),甚至都不需要知道φ(x)的具体形式。由于径向基函数的参变量少,且采用RBF核的SVM对频率较高的非线性系统有较好的逼近性能。另外,RBF核的参数在有效范围内改变时不会使空间复杂度过大[9]。因此,本研究将核函数取为径向基函数,即
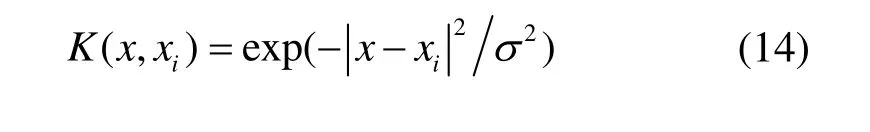
二、基于最小一乘的遗传算法参数寻优
不敏感损失函数中的ε、惩罚因子C和径向基函数中的2σ这三个参数取值的不同,将得到不同的支持向量回归模型。从而,这三个参数的取值将对回归模型的预测精度产生很大的影响。遗传算法对含参变量多且计算结果难以获得的复杂优化问题尤为适用[10]。本研究将采用自适应遗传算法对SVR的参数C,2σ和ε进行寻优。对传统的遗传算法,它能避免过早收敛,且具有更好的局部搜索能力和全局搜索能力。
本研究在求解的优化准则中,将采用最小一乘准则取代最小二乘准则。这是由于在应用最小二乘准则时,异常点的误差会被扩大化,且在样本数据较少时,预测精度会变低,而最小一乘准则具有较好的稳健性,它的统计性能要优于最小二乘准则[11]。
在采用最小一乘准则的参数优化步骤如下:
Step1:初始化种群大小,令 80N=,并随机产生N个个体 (C,σ2,ε)的取值,且编码方法采用二进制编码。
Step3:针对每个个体的适应度值,进行选择和复制运算,从而形成了一个临时的集合G。选择策略采用正比例选择策略,第i个个体被选择的概率为
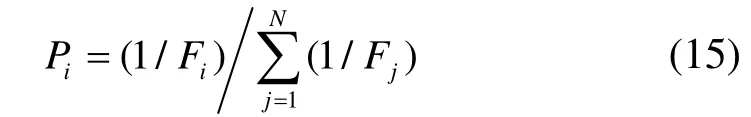
其中Fi为第i个个体的适应度值。在得到选择概率后,采用旋轮法来实现选择操作。即对于随机数ξ,当Ai-1≤ξ≤Ai时,则第i个个体被选择,其中
Step4:交叉运算采用多点交叉。交叉概率为
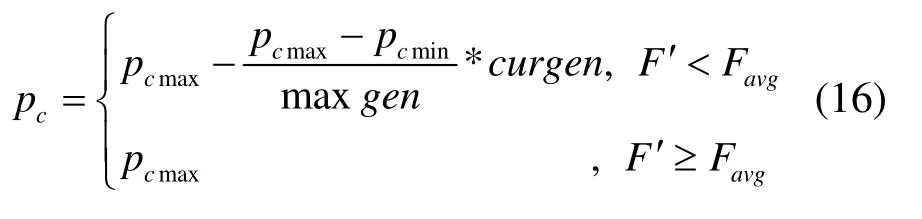
其中pcmax是最大交叉概率,pcmin是最小交叉概率,F′是两个个体中较小的适应度值,maxgen是最大迭代次数,curgen是当前迭代次数。为了获得较优的全局搜索能力,避免陷入局部最优,这里令pcmax=0.9,pcmin=0.1。
Step5:变异策略采用多点变异。概率如下:
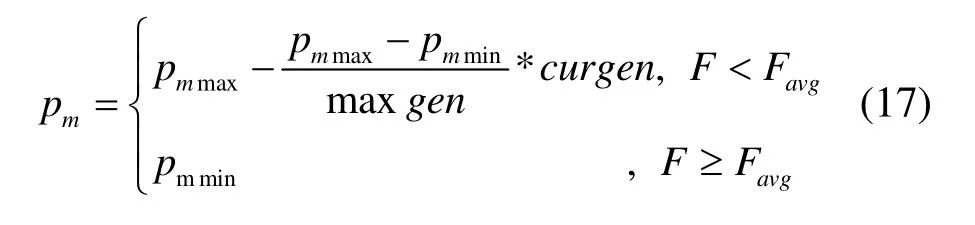
其中pmmax是最大变异概率,pmmin是最小变异概率,F是个体的适应度值。为了使个体在初始迭代过程中尽量多样化并且在后期迭代过程中有出色的局部搜索能力,这里令pmmax=0.4,pmmin=0.01。
Step6:判断是否达到终止条件,如何不是,则跳转到Step1。这里终止条件为迭代次数M=2000或者误差精度η=10-6。
Step7:输出最优参数集 (C,σ2,ε),得到预测模型f(x)。
三、建模和预测
(一)数据的选取及预处理
本研究的影响因素为上月用电量(亿千瓦时)、月平均温度(℃)、居民消费价格指数(CPI)、社会消费品零售额(亿元)、工业增加值(亿元)和进出口总额(亿元)等。通过对江苏省2004年1月~2009年7月的数据,采用交叉验证的思想,构建基于最小一乘准则下的GA-SVR模型,并对未来进行预测分析。
并利用公式
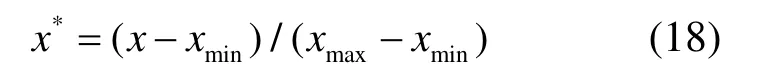
对数据进行标准化处理,以消除量纲的影响。
(二)模型的回归预测结果
本研究使用matlab进行建模分析,将江苏省2004年1月~2009年7月的宏观经济数据和全社会用电量数据作为训练集,进行模型训练。同时用2009年8月~10月的全社会用电量数据进行验证分析。为了有良好的训练速度,交叉验证的训练份数 4K=。从而采用基于最小一乘准则的GA-SVR方法拟合预测结果和相对误差如图1、图2所示。
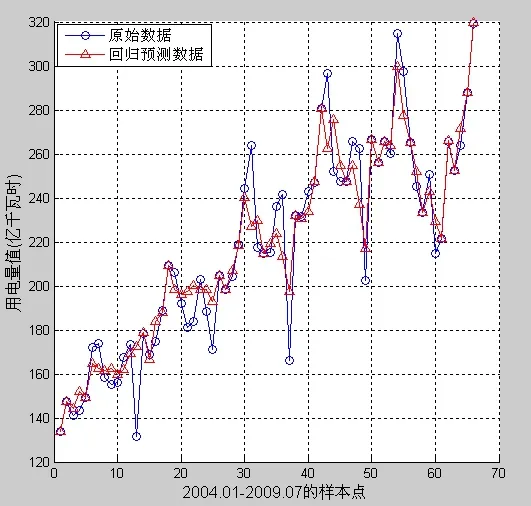
图1 基于最小一乘准则的回归预测结果对比
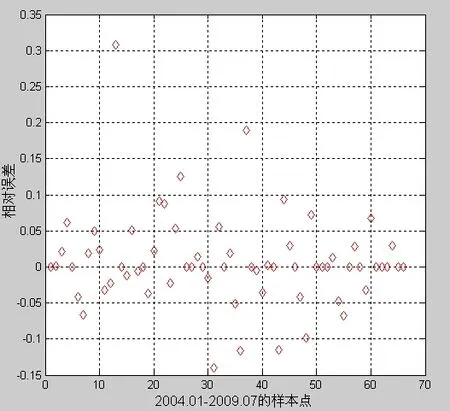
图2 相对误差
将本文模型与matlab工具箱中的BP-神经网络模型进行比较分析,结果见表2:
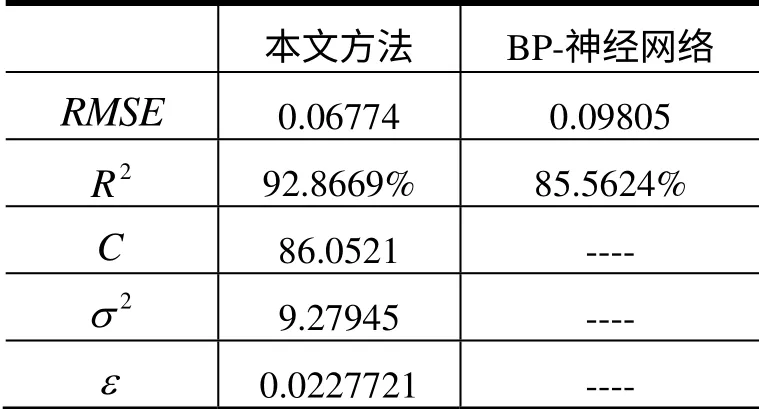
表1 拟合比较
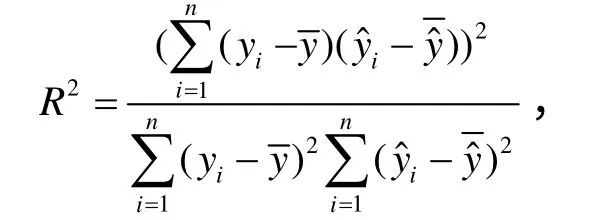
yi为真实值,为预 测值,
RMSE度量了模型误差的偏离程度,R2度量了模型的拟合程度。
本文模型与传统SVR方法、PSO-SVR方法比较,结果如表2所示。
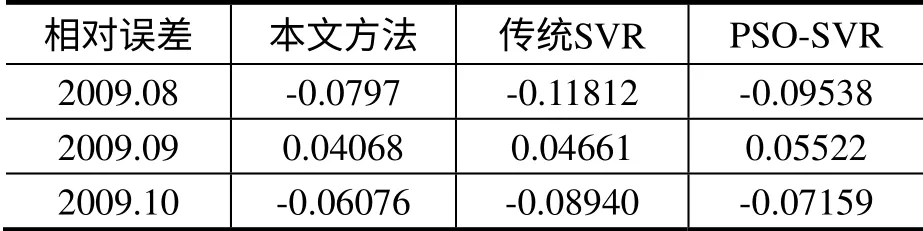
表2 预测结果比较
其中,相对误差rel=(-yi)yi,yi为真实值,为预测值。
从图1和图2可以看出,模型的训练精度还是比较高,总体上误差保持在10%以内。从表1的结果看出,基于最小一乘准则和交叉验证思想的GA-SVR模型的偏离程度和拟合精度都比BP-神经网络要好。同时,表2表明该方法在实验中的预测精度上也要比传统的SVR方法和PSO-SVR方法要精确。
四、结论
本研究提出了一种基于最小一乘准则和交叉验证思想的GA-SVR模型。该模型不同于一般的模型曲线拟合中采用的最小二乘方法,而是使用了最小一乘准则,从而可以避免异常点对模型总体的影响,提高模型的稳定性。接着利用自适应遗传算法对SVR模型进行参数寻优,加快了参数的择优速度,提高了模型的预测精度,同时通过交叉验证的思想,进一步提升模型的稳定性和泛化能力。虽然支持向量回归模型对非线性问题能有很好的拟合能力,但是与所预测问题选取的相关因素将对预测结果产生较大影响。因此,为了使模型提供更好的预测能力,应当选取更能反映问题本质的训练数据。同时,提高训练样本容量并且寻求更优的参数优化方法也将有助于提高模型的预测精度。
[1]VAPNIK V N.The Nature of Statistic Learning Theory[M].New York:Springer,1995.
[2]ZARNANI A,MUSILEK P,SHI Xiaoyu,et al.Learning to predict ice accretion on electric power lines[J].Engineering Applications of Artificial Intelligence,2012,25(3):609-617.
[3]KAVAKLIOGLU K.Modeling and prediction of Turkey’s electricity consumption using Support Vector Regression[J].Applied Energy,2011,88(1):368-375.
[4]HONG Wei-Chiang.Electric load forecasting by support vector model[J].Applied Mathematical Modelling,2009,33(5):2444-2454.
[5]NIU Dongxiao,WANG Yongli,et al.Power load forecasting using support vector machine and ant colony optimization[J].Expert Systems with Applications,2010,37(3):2531-2539.
[6]刘涵,刘丁,李琦.基于支持向量机的混沌时间序列非线性预测[J].系统工程理论与实践,2005,25(9):94-99.
[7]肖智,王明恺,谢林林,王伟立.考虑样本不平衡的多准则库存分类加权支持向量机方法及其参数选择[J].中国管理科学,2007,15(z1):29-34.
[8]石海波.PCA-SVM在电力负荷预测中的应用研究[J].计算机仿真,2010,21(10):279-282.
[9]荣海娜,张葛祥,金炜东.系统辨识中支持向量机核函数及其参数的研究[J].系统仿真学报,2006,18(11):3204-3208,3226.
[10]FRANK H F,LEUNG,H K,et al.Tuning of the Structure and Parameters of a Neural Network Using an Improved Genetic Algorithm[J].IEEE Transactions on Neural Networks,2003,14(1):79-88.
[11]陈希孺.最小一乘线性回归[J].数理统计与管理,1989,8(5):48-55.
[12]董春娇,邵春福,熊志华.基于优化SVM的城市快速路网交通流状态判别[J].北京交通大学学报,2011,35(6):13-16,22.
[13]王晓佳,沈建新,杨善林.基于Gauss插值的正交化预测方法在智能电网用电量预测中的应用研究[J].电力系统保护与控制,2010,38(21):141-145.
[14]杨海军,王太雷.基于模糊支持向量机的上市公司财务困境预测[J].管理科学学报,2009,12(3):102-110.
