螺旋桨射流对抛石基床冲刷的数值计算

李 勇，王元战，张宝华，梁鹏飞

（1.天津大学建筑工程学院天津市港口与海洋工程重点实验室，天津 300072；2.交通运输部天津水运工程科学研究所水工构造物检测、诊断与加固技术交通行业重点实验室，天津 300456）

螺旋桨射流对抛石基床冲刷的数值计算

李 勇1，王元战1，张宝华2，梁鹏飞1

（1.天津大学建筑工程学院天津市港口与海洋工程重点实验室，天津 300072；2.交通运输部天津水运工程科学研究所水工构造物检测、诊断与加固技术交通行业重点实验室，天津 300456）

抛石基床遭螺旋桨射流冲刷破坏而危及码头使用安全，是近几年码头检测评估工作中的新问题，国内海港工程设计规范中未考虑船舶尾流作用对抛石基床的冲刷影响。采用计算流体力学软件Fluent建立螺旋桨射流流场三维数值模型，并利用螺旋桨射流流速的理论研究成果对数值模型进行验证。通过数值模拟，研究螺旋桨射流在码头岸壁和基床底面影响下的变化规律，建立了船舶尾流在重力式码头前沿的最大冲刷流速及其位置的经验公式。

船舶尾流；螺旋桨射流；数值模拟；流速公式

Biography：LI Yong（1986-），male，master student.

抛石基床遭螺旋桨射流冲刷破坏而危及码头使用安全，是近几年码头检测评估工作中的新问题，目前设计规范中未明确规定港作大型拖轮对抛石基床冲刷破坏的验算条目，相应防范措施也不够完善。

欧洲科学家最早关注码头结构遭船舶尾流冲刷破坏的现象。1981年，瑞典专家Bergh和Cederwall考察发现瑞典25个港口因船舶的紊态射流冲刷而产生严重损害［1］。1987年，Chait调查南非港口的结构损伤情况时，发现伊利莎白港12号泊位5个沉箱单元有3个已经失稳［2］。直至2000年，营口港鲅鱼圈港区、秦皇岛港东区工作船码头、大连港大连湾4号泊位和大窑湾8号泊位相继出现抛石基床被高速水流冲刷淘空，乃至基床失稳的问题［3］，国内研究人员才真正开始关注螺旋桨尾流的冲刷影响。

欧洲科学家通过大量物理模型试验研究，对自由水域中，螺旋桨射流的机理有了一定了解，各国学者提出了很多流速分布公式。我国此类研究工作起步较晚，目前的研究工作主要为螺旋桨射流流速分布规律和块石稳定重量两个方面，具有代表性的是武汉科技学院的李剑超等研究船舶螺旋桨对水体底部污染物的扰动作用，建立关于射流初速度和特征长度的射流速度分布统一公式［4-5］，该公式建立在大尺度自由射流的基础上，不符合真实螺旋桨射流的特点；计算中求解特征半径需进行幂级数运算，求解难度较大，不适宜一般工程应用；天津大学孙建军［6］利用计算流体力学软件ADINA建立数值模型，模拟分析水流与块石相互作用，提出修正的块石启动流速，该论文基于抛石基床二维模型，无法准确描述三维流场中的流速分布状态；天津大学梁鹏飞［7］使用CFD软件Fluent建立三维数值模型，研究螺旋桨尾流对基床的冲刷影响，该论文未考虑螺旋桨不同转速条件对射流流场和基床附近流场的流速分布的影响，无法准确反映螺旋桨射流对块石的冲刷破坏机理。

本文利用CFD软件Fluent模拟三维螺旋桨射流场，建立螺旋桨射流对抛石基床冲刷的数值模型。将自由射流的模拟结果与经验公式的计算结果进行比较，验证了CFD软件Fluent建立螺旋桨射流模型的可行性和合理性。增加码头岸壁和基床底面2个边界条件，同时变化螺旋桨的转动速度，使射流场更接近实际情况。改变螺旋桨距海底的高度和距岸壁的距离，通过数值模拟得到螺旋桨在不同位置处射流流场的速度分布；根据数值模拟结果，得出抛石基床表面最大流速及其所在位置的经验公式。

1 螺旋桨射流经验公式

以往对螺旋桨射流的研究成果局限于自由水域，流场为桨轴线中心对称分布，整体呈圆锥形，分为起始段和主体段2个发展阶段（图1）：流场的起始段，靠近螺旋桨平面，桨轴线处受桨毂影响存在低速区［8］，断面最大流速出现在桨叶中部，流速分布呈双峰型；射流沿轴向发展过程中，桨毂影响逐渐减小，桨轴线上流速逐渐增大，侧向扩散的高速水流与低速区内的水流相互掺混，经过一段流程后，高速流体只向外扩散，桨轴线上出现唯一的最大流速，射流进入主体段，射流形态趋于稳定。

图1 螺旋桨射流发展过程图Fig.1 Schematic view of propeller jet

1.1 射流初速度

Albertson［9］等于1950年基于轴向动量理论，将螺旋桨射流简化为平面射流问题研究螺旋桨射流流速分布规律，得到螺旋桨射流初速度计算公式

将V0定义为射流初速度，n为螺旋桨转速，D为螺旋桨桨径，Ct为螺旋桨的推力系数。

Hamill［10］利用真实螺旋桨代替平面射流，对轴向动量理论进行修正，得到公式

Stewart［11］做了类似试验，得到了基于螺旋桨几何特点的射流初速度公式

式中：BAR为盘面比，即所有叶片的投影面积与螺旋桨盘面面积的比值；P/D为螺距比，即螺旋桨螺距与直径的比值。Hashmi［12］引入螺旋桨桨毂直径Dh，将公式改写为

1.2 起始断面流速衰减

Hamill发现最大流速只在x=0.35D之内的区域无衰减，之后的衰减满足公式

Hamill公式定义起始段长度为2D。

Stewart提出了线性的断面最大流速衰减公式，定义起始段长度为3.25D

1.3 起始断面流速分布

Hamill对Albertson的工作进行修正，得到计算射流起始段断面流速分布的2个公式

式中：Vx，r为螺旋桨射流区域中任意点的平均流速，其位置由该点距射流平面的轴向距离x和距旋转轴的径向距离r来定义。Rmo为螺旋桨初始流速距旋转轴的径向距离，一般

式中：Rp为螺旋桨半径；Rh为桨毂半径。Stewart通过起始段流速分布实验验证了该公式的合理性。

1.4 射流最大流速

螺旋桨射流主体段断面最大流速衰减的研究成果较多，计算最大流速的公式间存在较大差异，各公式数学表达式及适用范围详见表1。

表1 各种螺旋桨射流主体段断面最大流速经验公式Tab.1 Empirical equations for calculating maximum velocity within the zone of established flow

表2 螺旋桨几何参数Tab.2 Propeller geometry parameters

1.5 主体段速度分布

Albertson等提出了计算螺旋桨射流主体段断面流速分布的半经验公式，此公式 经 过 Fuehrer、Romisch、Hamill、Stewart 和McGarvey等人实验验证后得到肯定［16］

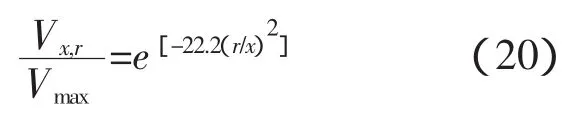
2 螺旋桨射流模拟方法

2.1 螺旋桨模型

选择结构简单、在船舶运输和科学研究领域均应用较广的DTMB-P4119型螺旋桨作为研究对象，表2为螺旋桨的基本几何参数。

利用三维造型软件UG建立螺旋桨模型，参考天津大学梁鹏飞等对螺旋桨尾流场数值模型的研究。利用Gambit生成螺旋桨实体模型。在Fluent中将螺旋桨外水域分为静水域和动水域两部分，构建旋转坐标系，将非定常流动转化为定常流动。考虑螺旋桨后方水体的影响，保证计算域尺度满足要求，建立流场域为长50 m，宽30 m，高20 m的长方体。

2.2 螺旋桨射流流态整体分析

将动水体设置为动参照系，螺旋桨置于距离码头岸壁40 m、距底面10 m的位置并施加300转/min的转速，得到螺旋桨在自由水域中的射流场。沿螺旋桨轴线方向（即射流模型x方向）和垂直于螺旋桨轴线方向（即射流模型y、z方向）可以分别提取桨轴线方向的速度分布和垂直于螺旋桨轴线方向上不同剖面的速度分布（图2）。根据数值模拟结果绘制断面最大流速曲线。桨面处断面最大流速为射流初速度，自桨面起5 m的范围内，由于高速水流与低速水流的强烈掺混，动能严重损失，断面最大流速从10.1 m/s减小到6 m/s，这一现象与紊动射流类似。随后流速断面逐渐扩大，断面上各质点速度值逐渐接近，流速下降趋势放缓。通过与Stewart公式计算得到的断面最大流速衰减曲线进行比较发现，在距桨面0～5 m范围内，两曲线斜率一致，断面最大流速衰减情况几乎相同。5 m后，在同一位置上，数值模拟得到的断面最大流速大于Stewart公式计算结果。因Stewart公式对应前文提到的射流起始段和主体段有不同的线性公式进行描述，故在桨后6.5 m处，即起始段与主体段的连接点处存在明显的拐点，且该式所规定的起始段长度为固定值。数值模拟得到的曲线与Stewart公式曲线吻合较好，同时更好地反映了射流流速的连续性。

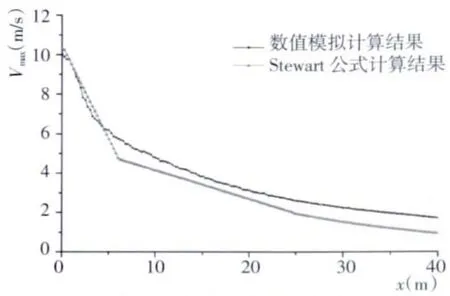
图2 断面最大流速比较Fig.2 Comparison of section maximum velocity

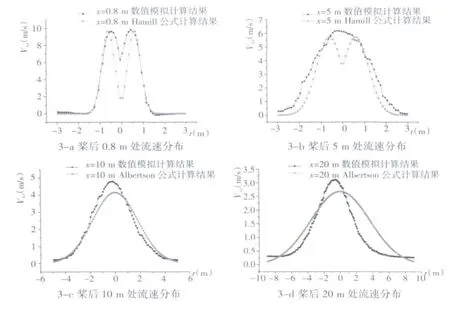
图3 断面流速分布比较Fig.3 Comparison of section velocity distribution

图3为各断面流速分布的对比，数值模拟的流速分布与经验公式计算结果在分布规律上基本一致，但在断面最大流速值及出现位置、流动区域面积以及轴对称情况等方面还存在一定差异。出现这些差异的原因，一方面是在建模时为便于运算而将模型简化，数模环境只能近似模拟实际情况；另一方面，实际螺旋桨几何形状变化较大、射流试验环境因素多变以及速度测量过程中不可避免的误差，导致同一经验公式无法精确反映任意螺旋桨射流情况。

沿螺旋桨轴线方向的速度分布是本文的主要研究对象。根据Fluent得到的模拟结果，将流速的结果数据导入后处理软件Tecplot，流场的整体形态和各点的轴向流速可以直观、清晰地反映在二维图形中。图4为Tecplot 中绘制的螺旋桨射流在z=0平面上的流速分布等值线图，可清晰看到螺旋桨起始段流速的双峰型分布。

图4 螺旋桨射流z=0平面流速等值线图Fig.4 Isogram of propeller velocity at z=0

3 螺旋桨尾流冲刷作用的统计分析

在 CFD软件 Fluent中，选择k-epsilon model，Materials中采用海水参数，螺旋桨的转动速度（n）分别采用 100、200、300 转/min，螺旋桨与岸壁之间的距离（x）分别取 5、6、7、8、9、10、11、12、13、14、15 m，与底面之间的距离（y）分别取 3、4、5、6、7、8、9、10 m，共计 384 种工况。得到的数据结果通过以下 2 种方式分析：（1）固定螺旋桨与底面之间的距离（y），改变螺旋桨与岸壁之间的距离（x）；（2）固定螺旋桨与岸壁之间的距离（x），改变螺旋桨与底面之间的距离（y）。总结底面冲刷流速最大值及其位置的规律，得到经验公式（为简便起见，本章图、表仅列出200、300转/min条件下的结果对比）。

3.1 螺旋桨位置在水平方向变化

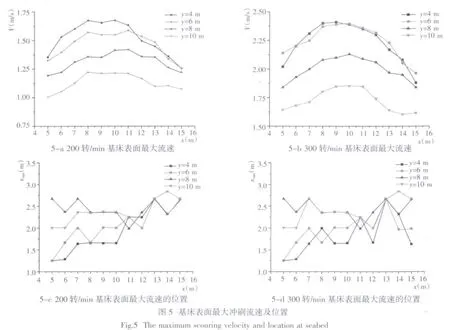
选取螺旋桨的某一转速条件（n）和螺旋桨与底面的间距（y），将螺旋桨与岸壁之间的距离（x）分别取5、6、7、8、9、10、11、12、13、14、15 m，利用 Fluent进行数值模拟，得到 12 种工况基床表面最大冲刷流速及其位置的坐标数据；选取下一个螺旋桨与底面的距离（y），重复上述工作。根据转速条件绘图，相关结果参见图5，图5-a、5-b分别为200、300转/min条件下基床表面最大冲刷流速的变化曲线，图5-c、5-d分别为200、300转/min条件下最大冲刷流速位置的变化曲线。

3.2 螺旋桨位置在竖直方向变化

选取螺旋桨的某一转速条件（n）和螺旋桨与岸壁的间距（x），将螺旋桨轴心距海底高度（y）分别取3、4、5、6、7、8、9、10 m，利用Fluent进行数值模拟，得到8种工况基床表面最大冲刷流速及其位置的坐标数据；选取下一个螺旋桨与岸壁的距离（x），重复上述工作。根据转速条件绘图，相关结果参见图6，图6-a、6-b分别为200、300转/min条件下基床表面最大冲刷流速的变化曲线，图6-c、6-d分别为200、300转/min条件下最大冲刷流速位置的变化曲线。

图6 基床表面最大冲刷流速及位置Fig.6 The maximum scouring velocity and location at seabed

3.3 拟合公式及规律总结

根据边界（码头岸壁和底面）对螺旋桨射流场的不同影响，将螺旋桨在水域中的空间位置大体划分为4个区域（图7）：受岸壁和底面共同影响（1），只受底面影响（2），只受岸壁影响（3），不受岸壁和底面影响（4）：

（1）受岸壁和底面共同影响（大致区域 x＜9.5 m，y＜5.5 m）：螺旋桨射流的下边界受到底面的约束影响，同时螺旋桨与岸壁距离较近，射流在初始段与岸壁发生相互作用，射流不能充分发展，极大的影响射流流速的增加，再加上岸壁回流与射流区的相互作用，基床表面的最大冲刷流速及冲刷核心区出现的位置具有不确定性。

（2）只受底面影响（大致区域 x＞9.5 m，y＜5.5 m）：螺旋桨射流的下边界受到底面的约束影响，射流一侧不能充分发展，加上回流与射流的相互作用，对底面回流流速的最大值及冲刷核心区出现的位置有一定影响。

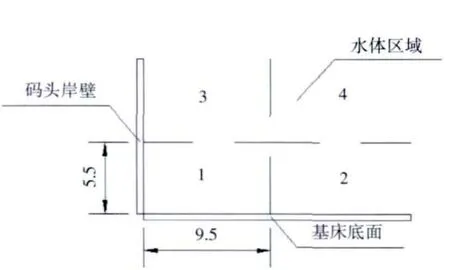
图7 螺旋桨位置的分区示意图Fig.7 Partition schemes of propeller′s position

（3）只受岸壁影响（大致区域x＜9.5 m，y＞5.5 m）：螺旋桨射流的边界基本不受底面的约束影响，但射流初始段与岸壁发生相互作用，导致射流流速不能充分发展，对底面回流的最大值有一定影响，但对冲刷核心区出现的位置影响较小。

（4）不受岸壁和底面的影响（大致区域x＞9.5 m，y＞5.5 m）：螺旋桨射流不受底面和岸壁的约束影响，射流充分发展，流速可以达到最大值，回流与射流基本不发生相互作用，基床表面最大冲刷流速及冲刷核心区出现的位置影响有明显规律。

综上所述，基床表面最大冲刷流速总体的分布规律比较明显：螺旋桨的位置由低到高，即螺旋桨与底面之间的距离（y）由小变大，底面回流的冲刷流速先增大后减小；螺旋桨位置逐渐远离岸壁，即螺旋桨与岸壁之间的距离（x）逐渐增大，底面回流的冲刷流速先增大后减小。根据流速分布规律，提出最大流速及其位置的公式为

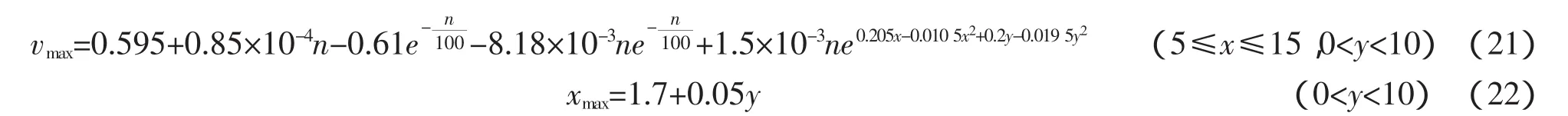
式中：vmax为基床表面最大冲刷流速，m/s；n为转速，转/min；x为螺旋桨与岸壁之间的距离，m；y为螺旋桨与底面之间的距离，m；xmax为最大冲刷流速与岸壁之间的距离，m。

将经验公式与数值模拟结果进行对比，经验公式的计算值比数模结果偏差在±3%以内。图8为x=7 m、x=10 m处，不同转速条件下，数模结果（smjg）与经验公式（jygs）计算结果的对比；表3为x=7 m、x=10 m时，不同转速条件下数模结果与经验公式计算结果及误差数值。

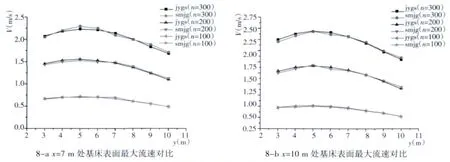
图8 数模结果与经验公式计算结果对比Fig.8 Comparison between numerical model and experience formula

4 结语

利用CFD软件Fluent建立螺旋桨射流三维数值模型，模拟、分析螺旋桨射流在码头岸壁和基床底面2个边界条件影响下的流速分布情况。将自由射流的模拟结果与经验公式的计算结果进行比较，验证了CFD软件Fluent建立螺旋桨射流模型的可行性和合理性。

在增加码头岸壁和基床底面2个边界条件的三维数值模型中，按一定规律改变螺旋桨在水中的位置，确定螺旋桨在不同位置时，基床表面射流最大冲刷流速及其位置，综合各种工况条件下的数值模拟结果，总结出统一的经验公式。该公式以三维流场的数值模拟结果为基础，考虑到旋桨不同转速条件对射流流场和基床附近流场的流速分布的影响，符合螺旋桨射流的一般特点，并且公式形式简单，求解难度不大，计算结果偏差较小，适宜一般工程应用，可为相关领域学者的研究或者规范修订提供有力参考。

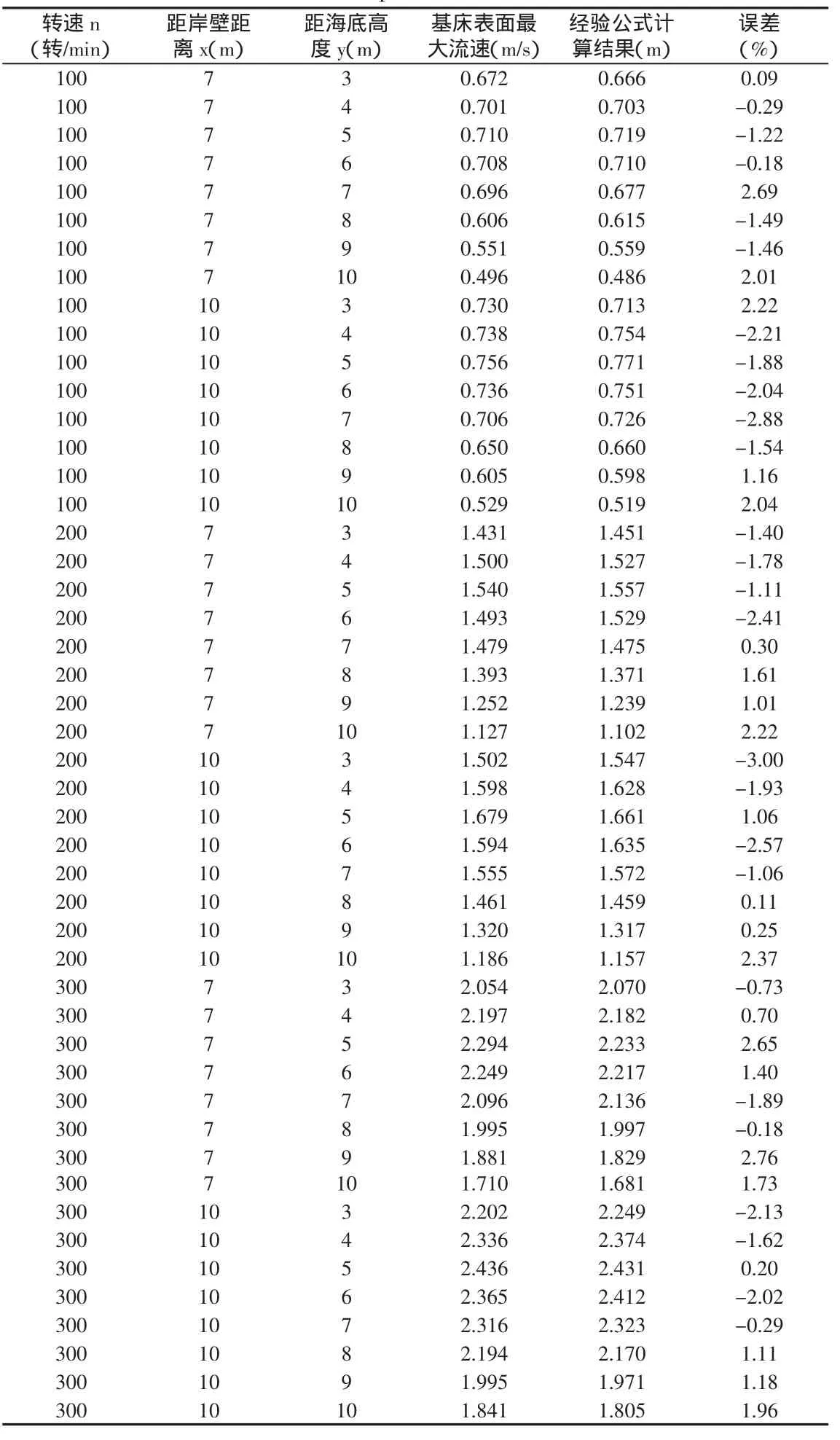
表3 流速误差对比Tab.3 Comparison of the error

［1］Bergh H,Cederwall K.Propeller erosion in harbours［R］.Sweden：Hydraulics Laboratory,Royal Institute of Technology,Stockholm,1981.

［2］Chait S.Undermining of quay walls at South African ports due to the use of bow thrusters and other propeller units［C］//Permanent International Association of Navigation Congresses.Bulletin of Permanent International Association of Navigation Congresses.Belgium：Permanent International Association of Navigation Congresses,1987.

［3］张宝华，黄敬东，王笑难,等.重力式码头抛石基床遭水流冲刷破损后的诊断和治理［J］.水运工程，2009（8）：49-53.

ZHANG B H,HUANG J D,WANG X N.Diagnosis and renovation to gravity wharf′s rubble bed damaged by water flow［J］.Port&Waterway Engineering,2009（8）：49-53.

［4］李剑超,褚君达.结合起始段的射流过程研究［C］//黄真理.中国环境水力学.北京：中国水利水电出版社,2002.

［5］李剑超，胡仁志，王波,等.船舶螺旋桨射流扰动下的污染底泥起悬研究［J］.环境科学与技术，2005，28（2）：6-8.

LI J C,HU R Z,WANG B,et al.Resuspension of Contaminated Bottom Sediment on Disturbing of Boat Propeller Jet Flow［J］.ENVIRONMENTAL SCIENCE&TECHNOLOGY,2005,28（2）：6-8.

［6］孙建军.船舶尾流作用下抛石基床块石冲刷稳定性研究［D］.天津：天津大学,2010.

［7］梁鹏飞.船舶尾流流速分布及其作用下抛石基床快事稳定性计算方法研究［D］.天津：天津大学,2011.

［8］Fuehrer M,Romisch K.Effects of modern ship traffic on islands and ocean waterways and their structures［C］//Permanent International Association of Navigation Congresses.Proceedings of Permanent International Association of Navigation Congresses.Leningrad：Permanent International Association of Navigation Congresses,1977,Sections 1-3.

［9］Albertson M L,Dai Y B,Jensen R A,et al.Diffusion of submerged jets［C］//Ametican Society of Civil Engineers.Proceedings of the American Society of Civil Engineers.US：Ametican Society of Civil Engineers,1950.

［10］Hamill G A.Characteristics of the screw wash of a manoeuvring ship and the resulting bed scour［D］.UK：Queen′s University of Belfast,1987.

［11］Stewart D P J.Characteristics of a ships screw wash and the influence of quay wall proximity［D］.UK：Queen′s University of Belfast,1992.

［12］Hashmi H N.Erosion of a granular bed at a quay wall by a ship′s screw wash［D］.UK：The Queen′s University of Belfast,1993.

［13］Verhey H J.The stability of bottom and banks subjected to velocities in the propeller jet behind ships［C］//International Harbour Congress.Proceedings of the 8th International Harbour Congress.Antwerp,Belgium：International Harbour Congress,1983.

［14］Blaauw H G,Kaa E J van de.Erosion of bottom and sloping banks caused by the screw race of manoeuvring ships［C］//International Harbour Congress.Proceedings of the 7th International Harbour Congress.Belgium：International Harbour Congress,1978.

［15］Hashmi H N.Erosion of a granular bed at a quay wall by a ship′s screw wash［D］.UK：The Queen′s University of Belfast,1993.

［16］Lam W,Hamill G A,Song Y C,et al.A review of the equations used to predict the velocity distribution within a ship′s propeller jet［J］.Ocean Engineering,2010,38（1）：1-10..

Numerical simulation of flushing action on rubble bed under scouring effect of ship stern flow

LI Yong1,WANG Yuan-zhan1,ZHANG Bao-hua2,LIANG Peng-fei1
（1.School of Civil Engineering,Tianjin Key Laboratory of Port and Ocean Engineering,Tianjin University,Tianjin300072,China；2.Tianjin Research Institute for Water Transport Engineering,Key Laboratory of Harbor&Marine Structure Safety,Ministry of Transport,Tianjin300456,China）

Ship stern flow leads to the destruction of gravity wharf′s rubble bed,which is gradually becoming a new problem in terminal testing evaluation.The effect of ship stern flow on rubble bed stability is not estimated in the code of harbor and coastal engineering design in China.Using computational fluid dynamics software Fluent,a three dimensional numerical model of propeller jet flow field was established,and the propeller jet velocity distribution results were validated by the study of the marine propeller jet velocity theory at home and abroad.With the results of numerical simulation,the variation laws of the propeller jet under the influence of wharf shore wall were obtained,and the empirical formula of the maximum scour flow velocity and its location were proposed.

ship stern flow;propeller jet;numerical simulation;velocity formula

U 661.1；O 242.1

A

1005-8443（2013）03-0185-08

2012-07-30；

2012-10-17

国家自然科学基金（50979069）；天津市科技支撑计划重点项目（10JCYBJC03400）；天津市应用基础及前沿技术研究计划（10SYSYJC27300）

李勇（1986-），男，吉林省抚松县人，硕士研究生，主要从事港口与近海工程研究。