到达时间与工期同序的串行批处理机排序问题

岳雅娟，赵玉芳，许 尉

（沈阳师范大学 数学与系统科学学院，沈阳 110034）

0 引 言

在芯片等电子产品制造系统中，常常把在前一道工序加工完的工件放到货盘里，把同一货盘中的工件作为一批，一起放到处理机上依次加工，这就相当于在本道工序中工件是动态到达的，并且批的加工时间等于此批中所有工件的加工时间之和，只有当货盘中的所有工件都加工完后才可以交货，相当于批中每个工件的完工时间都相同，等于此批中最后一个工件的完工时间。在实际生产过程中，一般工件都有一个交货期，其重要程度由权来决定。本文研究的问题是带有2个不同的到达时间，目标是使得未按时完工工件的总权值最小。

对于批处理机排序问题，Webster等［1］进行了综述。根据加工特点可将批处理机排序问题分为并行批（p－batch）模型、串行批（s－batch）模型［2］及半连续批（c－batch）模型。并行批模型是由 Lee［3］等根据半导体烤箱模型提出的，每批的加工时间为此批中所有工件的加工时间最大者。当所有工件的加工时间相等且到达时间与工期同序时，他们分别给出了极小化误工工件数∑Uj及最大误工Tmax问题的多项式动态规划算法。Lee等［4］给出了带有2个到达时间的最大完工时间问题的拟多项式动态规划算法，Liu等［5］进一步证明了这个问题是一般意义NP难的。文献［6－9］也对这类批处理机排序问题进行了研究。文献［10］从钢铁工业加热炉对管坯的加热过程中提出了一种半连续型批处理机排序问题，文献［11］研究了链式约束下半连续型批处理机排序问题。

本文研究的问题与上述问题不同，主要创新点为：所有工件只有2个不同的到达时间，而工期、加工时间及权可有多个不同值，并且到达时间与工期同序（即ri≤rj，有di≤dj），目标为极小化加权误工工件数，这个问题目前还没有人研究过。

1 问题描述

化加权误工工件数∑wjUj问题，用三参数表示法表示为－batch，rj∈｛0，r｝，agr（rj，djwjUj。

为了叙述方便，先来介绍一些符号。N表示要进行加工的n个工件构成的集合，S0表示在r0时刻到达的工件构成的集合，S1表示在r1时刻到达的工件构成的集合；N0表示在r0到r1之间开始加工的批构成的集合，N1表示在r1或r1之后开始加工的批构成的集合。则S1中的工件只能在N1中加工，而S0中的工件可能在N0中加工，也可能在N1中加工。并且S0∪S1＝N，S0∩S1＝Ø，N0∩N1＝Ø。

下面给出本文用到的的定义：

定义1 一批中所有工件的最小工期称为此批的工期；由按时完工工件构成的批称为按时完工批。也就是说，若一批的完工时间不超过这批的工期，则这批为按时完工批。

定义2 对于一个排序中的任意两批P和Q，若批P在批Q前加工，意味着不存在这样的工件i和j，使得i∈P，j∈Q且di＞dj，则称此排序为批EDD序。

为了说明上述符号及定义，先来看一个例子。

例 设有8个工件，到达时间r＝（0，0，0，0，0，0，10，10），加工时间p＝（4，1，2，1，6，2，3，3），工期d＝（4，6，8，11，13，21，22，25），s＝1。

若对工件分批为B1＝｛J1｝，B2＝｛J2，J3，J4｝，B3＝｛J5｝，B4＝｛J6，J7，J8｝，则S0＝｛J1，J2，J3，J4，J5，J6｝，S1＝｛J7，J8｝。按照图1所示分批及安排各批的加工顺序，有N0＝｛B2，B3｝，N1＝｛B4，B1｝，按时完工的批为B2，B3，B4，误工批为B1。

具体问题描述如下：设有n个工件J1，…，Jn，要在一台批处理机上进行加工，这n个工件构成的集合为N。有2个不同的到达时间r0，r1，不失一般性，设r0＝0，r1＝r＞0。工件Jj的到达时间为rj（rj∈｛0，r｝），加工时间为pj，工期为dj，完工时间为Cj；若Cj＞dj，称工件Jj误工，有Uj＝1；否则称工件Jj按时完工，有Uj＝0；权为wj，j＝1，…，n。批处理机的容量无限，即批处理机能将B（B＞n）个工件作为一批同时加工。只有当同一批中的工件都到达后，这一批才可以开始加工。在每一批开始加工之前都有一个固定的调整时间s，即批调整时间。在批的调整时间内机器不能加工任何工件，每一批内的工件间没有调整时间。假设所有数据都为非负整数。批的加工时间为此批中所有工件的加工时间之和，同一批中所有工件的完工时间都相等，为此批中最后一个工件的完工时间，称为批的完工时间。对于极小

图1 工件的加工时间表

2 最优解性质

Hochbaum等［13］证明了带有非负安装时间s及一个共同工期d，极小化加权误工工件数∑wjUj的单机批处理机排序问题是NP难的。显然，带有2个不同到达时间的问题1－batch，rj∈｛0，r｝，agr（rj，djwjUj至少也是NP难的。下面给出此问题的最优解的性质。

证明 用反证法。假设存在一最优排序，其中按时完工批l中的工件Jl1，Jl2，…，Jlk不按EDD序排列。不妨设工件Jli，Jlj（1≤i＜j≤k），Jli在Jlj前加工，而dli＞dlj。交换这两个工件，由于交换工件不改变这批的加工时间，所以交换后批l的完工时间与交换前相等，即工件Jli和Jlj的完工时间不变。又因为批l的工期不变，所以工件Jli和Jlj仍按时完工，交换后目标函数值不增加，故交换后仍是最优排序，其中同一按时完工批中的工件都按EDD序排列。

证明 1）首先用反证法证明N0中按时完工的批是按批EDD序排列的。

假设存在一个最优排序π，N0中按时完工的批不按批EDD序排列，则在此排序中，存在两相邻批P和Q，批P和批Q的工期分别为dP和dQ，P在Q前加工，且dP＞dQ，由批的工期的定义，不妨设工件i和j，i∈P，j∈Q，使得dP＝di，dQ＝dj，则di＞dj。

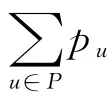
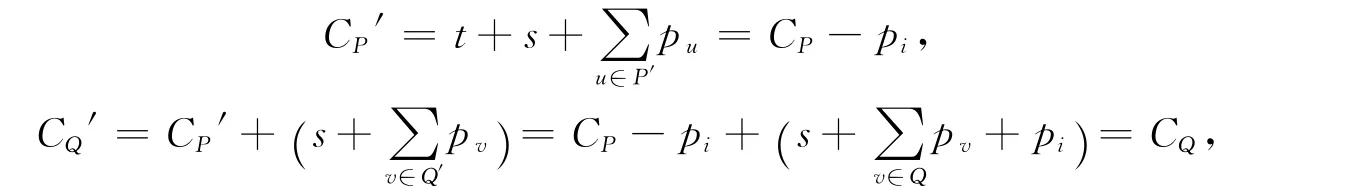
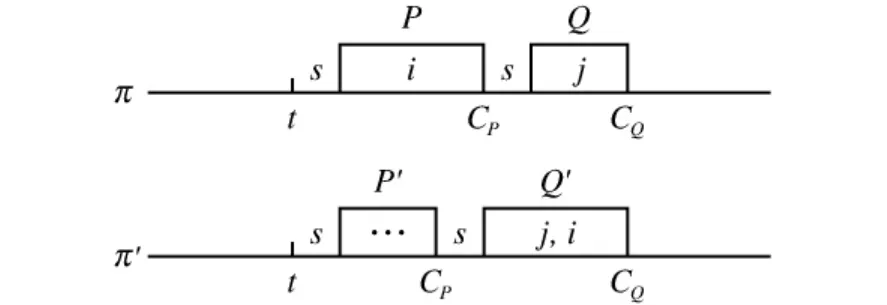
图2 π和π′的工件加工时间表

由此可得批P′的完工时间提前了，则批Q′的开始加工时间提前了，但完工时间不变。故调换后除工件i外，其他工件的完工时间都不大于调换前的完工时间，从而它们都不误工。调换后工件i和j在同一批中加工，因此工件i和j的完工时间相等，即C′i＝C′j＝CQ。而工件j按时完工，即Cj′≤dj，又C′j＝C′j，dj＜di，所以工件i也按时完工。如图2所示。

2）下面来看N1中的情况。N1中的批在r1或r1之后开始加工，此时所有工件都已到达。与证明1）类似，可得N1中按时完工的批也按批EDD序排列。

因此，任意一个最优排序都可通过上述调换使N0和N1中所有按时完工批都按批EDD序排列。

证明 由性质2，N0和N1中按时完工的批分别按批EDD序排列，又S1中的工件在r1＝r时刻到达，只能在N1中加工，故只需考虑S0中的工件在N1中加工的情况即可。

用反证法。假设存在一个最优排序π，其中2个按时完工批P和Q不按批EDD序排列。设批P和Q的工期分别为dP、dQ，加工时间分别为PP、PQ，完工时间分别为CP、CQ，且P∈N0，Q∈N1，dP＞dQ。不失一般性，假设P是N0中最后一个按时完工批，Q是N1中第一个按时完工批，t为批P的开始加工时间。下面考虑两种情况：

1）批P和Q中所有工件都在S0中。则CP＝t＋s＋PP，CQ＝CP＋s＋PQ＝t＋s＋PP＋s＋PQ≤dQ。现将π做变动如下：把批Q中的工件都移到批P中，新批设为P′，且P′中工件按EDD序排列，其余批及各批加工顺序不变，从而得到另一个排序π′。在π′中，C′p＝t＋s＋PP＋PQ＜CQ≤dQ＝d′P，故调换后仍为按时完工批，其余批开始加工时间不增加，仍然按时完工。

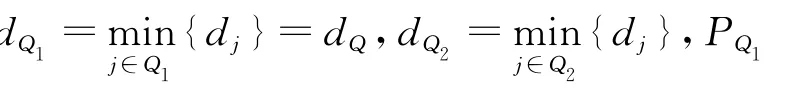
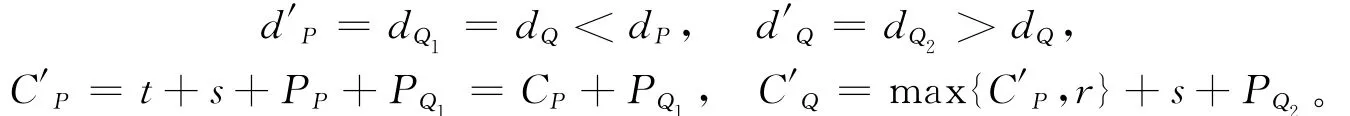
故CP＜C′P。则C′P、CP与r有以下3种大小关系。

a）若C′P＞r且CP＞r，则CQ＝max｛CP，r｝＋s＋PQ＝CP＋s＋PQ，

b）若C′P＞r且CP≤r，则CQ＝max｛CP，r｝＋s＋PQ＝r＋s＋PQ，

c）若C′P≤r，一定有CP＜r，则CQ＝max｛CP，r｝＋s＋PQ＝r＋s＋PQ，

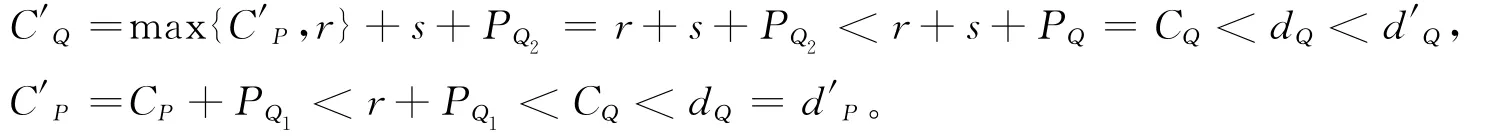
由以上分析可得：调换后P和Q中工件仍按时完工；其他批开始加工时间不增加，仍然按时完工；这样经过有限次调换，得到新排序，其所有按时完工批都按批EDD序排列，目标函数值不增加，故仍是最优排序。

由于所有工件的到达时间与工期同序，由上述3个性质可得以下推论。

3 动态规划算法

根据上述推论，将工件按EDD序重新排列。Cj（W，t，d）表示已排序的工件1，…，j的加权误工工件数为W，且最后按时完工批的开始加工时间为t、工期为d的最后按时完工工件的最小完工时间。Cj（W）表示Cj（W，t，d）中的最小者，即加权误工工件数为W的已排序的工件1，…，j中最后按时完工工件的最小完工时间。下面考虑工件1，…，j的任一最优排序。当工件1，…，j－1排完后，工件j的排列情况如下。

若工件j在S0中，则有5种可能的情况：

1）工件j误工；

2）工件j排在了N0中最后一个按时完工批中的末尾，隐含着工件j的完工时间不超过此批的工期；

3）工件j在N0中单独形成一个新批，在它的工期dj前完工；

4）工件j排在了N1中最后一个按时完工批中的末尾；

5）工件j在N1中单独形成一个新批，在它的工期dj前完工。

若工件j在S1中，则有3种可能的情况：

1）工件j误工；

2）工件j排在了N1中最后一个按时完工批中的末尾；

3）工件j在N1中单独形成一个新批，在它的工期dj前完工。

通过以上分析，工件j的排序可归纳为以下两种情况：

1）工件j误工。工件1，…，j－1的加权误工工件数为W－wj，所以Cj（W，t，d）＝Cj－1（W－wj，t，d）；

2）工件j不误工，也就是Cj（W，t，d）≤dj，有下面两种情况：

① 工件j排在当前排序的最后一个按时完工批中的末尾，即Cj－1（W，t，d）＞0。只有当工件都到达后才可以进行加工，故t≥rj。此时工件j的最小完工时间为Cj（W，t，d）＝Cj－1（W，t，d）＋pj。由于工件的到达时间与工期同序，所以排完j后，最后按时完工批的工期仍为d，即Cj（W，t，d）≤d。

② 工件j单独形成一个新批，也就是 max｛Cj－1（W，k，b），t｝＋s＋pj≤d（0≤k≤t，b∈｛d1，…，dj－1｝），此时d＝dj。其完工时间为t＋s＋pj，其中t≥Cj－1（W，k，b）且t≥rj。下面具体分析t的取值。若工件j在N0里单独形成一个新批，此时rj＝0，t＝Cj－1（W，k，b）；若工件j在N1里单独形成一个新批，当rj＝0时，t＝max｛Cj－1（W，k，b），r｝；当rj＝r时，t＝max｛Cj－1（W，k，b），r｝；所以若工件j单独形成一个新批，对于0≤k≤t，b∈｛d1，…，dj－1｝，其完工时间为 max｛Cj－1（W，k，b），t｝＋s＋pj。对于t＜min｛Cj－1（W，k，b），rj｝，此时要么机器不空闲，要么工件未到达，故定义Cj（W，t，d）＝＋∞。

由此可以得到以下的动态规划算法（DP）：

步骤1 把工件按EDD序排列，即d1≤d2≤…≤dn；

步骤4 计算Cj（W）＝min｛Cj（W，t，d）｝；

步骤5 若j＝n，计算W＊＝min｛W：Cn（W）＜＋∞｝，利用反向追踪得到所有工件的一个最优分批，再把误工工件以任意顺序排在最后按时完工批的后面加工。否则，令j＝j＋1，转步骤3。

下面来分析此动态规划算法的复杂性。

4 结 论

本文主要研究了工件带有2个不同的到达时间，且到达时间与工期同序的极小化加权误工工件数的单机串行批处理机排序问题，说明了此问题是NP难的，分析了最优解的性质，并给出了拟多项式动态规划算法及其时间复杂性。进一步，这个问题的FPTAS的设计，以及对于有多个到达时间，加工时间与工期同序或到达时间与工期同序等问题也具有较强的实际背景和理论意义，还有待研究。

［1］WEBSTER S，BAKER K R.Scheduling groups of jobs on a single machine［J］.Oper Res，1995，43：692－703.

［2］唐国春，张峰，罗守成，等.现代排序论［M］.上海：上海科学普及出版社，2003.

［3］LEE C Y，UZSOY R，MARTIN－VEGA L A.Efficient algorithms for scheduling semiconductor burn－in operations［J］.Oper Res，1992，40：764－775.

［4］LEE C Y，UZSOY R.Minimizing makespan on a single batch processing with dynamic job arrivals［J］.Int J Prod Res，1999，37：219－236.

［5］LIU Zhaohui，YU Wenci.Scheduling one batch processor subject to job release dates［J］.Disc Appl Math，2000，105（1／2／3）：129－136.

［6］BRUCKER P，GLADKY A，HOOGEVEEN H，et al.Scheduling a batching machine［J］.J Sched，1998，1：31－54.

［7］DENG X T，POON C K，ZHANG Y Z.Approximation algorithms in batch processing［J］.J Comb Opt，2003，7：247－257.

［8］LIU Zhaohui，CHENG T C E.Approximation schemes for minimizing total（weighted）completion time with release dates on a batch machine［J］.Theor Comp Sci，2005，347（1／2）：288－298.

［9］CONDOTTA A，KNUST S，SHAKHLEVICH N V.Parallel batch scheduling of equal－length jobs with release and due dates［J］.J Sched，2010，13：463－477.

［10］赵玉芳，唐立新.极小化最大完工时间的单机连续型批调度问题［J］.自动化学报，2006，32（5）：730－737.

［11］赵玉芳.链式约束下的一种半连续型批处理机调度问题［J］.沈阳师范大学学报：自然科学版，2010，28（3）：335－338.

［12］钟雪灵.基于动态规划的分批排序算法［J］.计算机工程与应用，2010，46（7）：229－231.

［13］HOCHBAUM D S，LANDY D.Scheduling with batching：minimizing the weighted number of tardy jobs［J］.Oper Res Lett，1994，16：79－86.

［14］BRUCKER P，KOVALYOV M Y.Single machine batch scheduling to minimize the weighted number of late jobs［J］.Math Meth Oper Res，1996，43：1－8.

［15］CHENG T C E，KOVALYOV M Y.Single machine batch scheduling with sequential job processing［J］.IIE Transactions，2001，33：413－420.

［16］BAPTISTE P.Batching identical jobs［J］.Math Meth Oper Res，2000，52：335－367.