基于模糊控制的塔式起重机定位和防摆仿真实验
2013-05-16张自强
游 谊, 张自强, 董 燕, 胡 伟
(1.上海师范大学信息与机电工程学院,上海201418;2.阿克苏职业技术学院,新疆阿克苏 843000)
0 引言
塔式起重机作为一种现代搬运机械,以其方便快捷、省时省工、占地面积小、结构简单等优点,广泛应用于现代厂房、建筑工地、岸边装卸等生产的各个领域。随着自动化控制以及计算机管理系统的广泛应用,塔式起重机从单一的搬运工具逐步演变成自动化,柔性化生产中的重要组成部分[1-2]。然而,要对塔式起重机运行位置精确控制相当困难,这是因为在起重机运行过程中受到小车加减速、风力等影响,负载会产生很大的摆动,这种摆动不仅会对负载的装卸难以定位,严重时还会影响生产效率,并存在着安全隐患。于此同时,随着经济全球化的快速发展,作为重要搬运工具的起重机正向着高参数、大型化发展,起重机构的运行速度和提升高度也得到大幅地提高,这就容易引起起重机在运行过程中加剧摆动程度,因而起重机定位和负载防摆困难的问题就突显出来。国内外许多专家在塔吊的防摆控制方法上进行了深入研究。例如经典控制,最优控制,自适应控制等[3-5]。但是,由于起重机控制具有非线性的特点,而这些控制方法都较依赖系统的状态向量和起重机的数学模型,所以难以进行有效地控制。然而,模糊控制在最近的短短10多年来发展相当迅速,这主要归结于模糊控制器具有一些明显优点。不需要知道被控对象的数学模型,控制规则来自于专家知识或熟练操作者的成熟经验,具有良好的鲁棒性和适应性。模糊控制在针对控制对象的复杂性,非线性,滞后性和耦合性上,具有良好的控制效果[6-7]。
文中针对起重机模型的非线性和不确定性,设计了一种基于模糊的起重机定位和防摆控制系统,其中利用模糊PID控制器控制小车的位移,模糊控制器调整负载摆角。因而有效地提高了系统的控制性能和响应速度,具有较好的鲁棒性。
1 起重机的数学模型
起重机防摆系统是一个典型的动力学系统,根据其力学特性,采用分析力学中的拉格朗日(Lagrange)方程来建立起重机防摆系统的数学模型[8-10]。

图1 起重机简化模型
塔式起重机的简化模型如图1所示。根据拉格朗日方程对起重机防摆系统进行受力分析得:

式中:M为小车质量;m为负载质量;l为悬绳的绳长;θ为悬绳摆角;系统受到的外力有小车驱动力F,钢丝绳起升力F1,小车与轨道之间的摩擦力f。假定塔吊负载水平运动过程中消摆控制,不考虑负载的提升,即绳长不变的情况,有

可得到定绳长的起重机防摆系统的数学方程为
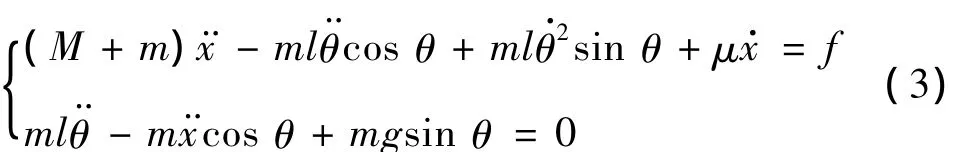
由于吊车运行中摆角不会超过10°,且平衡位置时θ=0,式(1)进一步简化得:
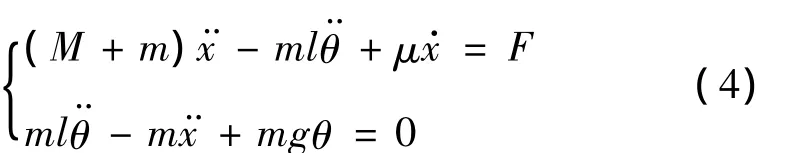
本实验的控制目标是通过控制电机驱动小车带动负载安全到达指定位置,同时做到定点准确和负载无摆动。也就是要求小车在给定一个行走距离参考值的情况下达到指定位置,同时实现悬绳摆角到达指定位置时减小到零。
2 起重机控制系统组成及工作原理
塔式起重机防摆系统是非线性的,传统的PID控制器实质上是一种线性控制器[11-12]。在工业生产过程中,许多被控对象受到负载变化或干扰因素影响,其对象特性参数或结构也会随之发生改变,对于这类复杂系统,传统PID控制器难以满足实际的需求,随着技术发展,模糊PID控制有效地解决了对复杂系统的控制问题。将操作人员的实际经验编辑成模糊规则,运用模糊推理,即可自动实现对PID参数的最佳调整,满足不同时刻的调节要求,因此可以被应用于塔式起重机的自动控制中[13-16]。为了研究方便,不考虑绳长的变化,模糊PID控制方法采用的系统模型是式(4)的非线性模型。引用模糊PID控制设计了两个控制器分别对小车位移和负载摆动进行控制。控制系统的原理图如图2所示。

图2 模糊PID控制系统原理图
其中,模糊PID控制器是基于一个初始设定的距离,从而对小车的位置进行有效控制。模糊控制器根据输入的位移偏差和偏差变化率,通过查阅模糊规则,推理出对应的kp,ki,kd,PID控制器再根据这三个参数调整输出相应的控制力U1。输入输出的模糊分割数都是7。
控制规则为:如果e为负大,ec为负大,则kp为正大,ki为负大,kd为正小等等,具体模糊规则如图3所示。

图3 模糊PID位移控制器模糊规则
系统框图中,模糊防摆控制器是用来消除负载的摆角,控制规则也是根据操作人员的实际经验归纳总结出来的。模糊防摆控制器有两个输入:摆角θ,摆角速度dθ/dt,输出为控制作用力U2。模糊防摆控制器模糊规则如图6所示。模糊防摆控制器输入输出的分割数也为 7,即:NB(负大),NM(负中),NS(负小),ZE(零),PS(正小),PM(正中),PB(正大);它们的隶属函数图如图3﹑图4所示。

图4 模糊防摆控制器输入

图5 模糊防摆控制器输出
控制规则可表述如下:如果摆角θ为负大,摆角速度dθ/dt为负大,则输出控制力U2为负大等,具体控制规则如图6所示。

图6 模糊防摆控制器模糊规则
3 实验结果与分析
为了验证系统的可行性,本实验对模糊PID控制算法进行了仿真研究,并和PID算法进行对比,仿真结果证明了该方法的可行性和良好的控制效果。塔式起重机的模型参数如下:小车质量M=3 kg,负载质量m=0.2 kg,绳长 l=1 m。
在相同的实验条件下,图7和图9给出了采用PID控制的仿真结果。图8和图10是模糊PID控制方法的负载摆角和小车位移的仿真结果。通过对比可以发现,模糊PID摆角曲线的超调量小于PID摆角曲线约0.2 rad,响应时间也减少了1.7 s,在缩短响应时间和减小摆角幅值方面,后者更有利于防止事故的发生。再对比位移曲线,虽然PID控制的位移曲线超调也小于1%,但是模糊PID响应时间却缩短了1.9 s,在快速制动定点停车上,模糊PID控制更胜一筹。从仿真图中不难看出,和PID控制相比,模糊PID控制能够更有效的抑制负载摆动,对小车的快速准确定位也具有更大的优势。
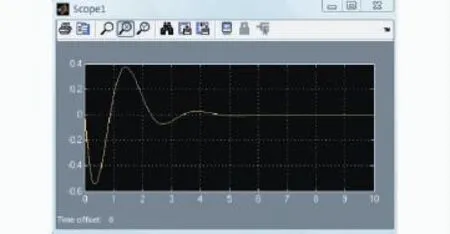
图7 PID控制:摆角曲线

图8 模糊PID控制:摆角曲线
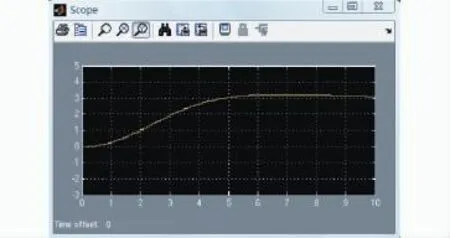
图9 PID控制:位移曲线
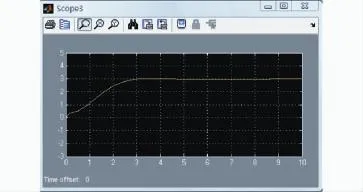
图10 模糊PID控制:位移曲线
4 结语
文中对塔式起重机的定位和防摆经行了研究,采用模糊控制实现PID参数的实时整定,克服了经典控制对数学模型的过渡依赖,为实现复杂系统的控制提供了有效途径,同时也提高了稳态精度和收敛速度。通过对小车位置和负载摆动进行实时控制,本实验取得了良好的控制效果。
(References):
[1] 刘金琨.先进PID控制及其Matlab仿真[M].2版.北京:电子工业出版社,2005.
[2] 薛 朵,李宇成.港口集装箱吊车的建模与模糊控制[J].机电一体化,2000,6(3):42-46.
[3] 华克强.桥式吊车模糊防摆技术[J].中国民航学院学报,2000,18(3):12-15.
[4] 李 伟.基于时间最优的起重机消摆控制策略[J].山东工业大学学报,1998.28(2):107-111.
[5] 薛定宇,陈阳泉.基于MATLAB/Simulink的系统仿真技术与应用[M].北京:清华大学出版社,2003.
[6] 樊 京,刘叔军,盖晓华,等.MATLAB控制应用与实例[M].北京:清华大学出版社,2008.
[7] 姜兴华,尹志宇,郭 晴.一种模糊自整定PID控制器的设计与仿真[J].河北师范大学学报(自然科学版),2009,33(4):448-450.
[8] 马晓虹.一种模糊自适应PID控制器的设计[J].大庆师范学院学报,2009,29(3):37-39.
[9] 曾光奇,胡均安,王 东,等.模糊控制理论与工程应用[M].武汉:华中科技大学出版社,2006.
[10] 席爱民.模糊控制技术[M].西安:西安电子科技大学出版社,2008.
[11] 王 宏,黎亚元,陈守强,等.起重机模糊控制系统的研究[J].机电工程技术,2006,35(9):18-20.
[12] 蒋 理,陈树广.基于模糊控制的桥式起重机定位防摆研究[J].计算机仿真,2009,26(6):179-182.
[13] 但堂咏.岸边桥式起重机智能防摇机理研究[D].武汉:武汉理工大学,2005.
[14] 王正林,王胜开,陈国顺.MATLAB/Simulink与控制系统仿真[M].北京:电子工业出版社,2005.
[15] 石辛民,郝整清.模糊控制及其MATLAB仿真[M].北京:清华大学出版社,2008.
[16] 张 静.MATLAB在控制系统中的应用[M].北京:电子工业出版社,2007.
