聚合物驱流线模拟中的更新流线问题

汤昌福，王晓冬，刘翰林，王军磊

(1.中国地质大学(北京)，北京 100083;2.中石油勘探开发研究院，北京 100083)

引 言

聚合物作为提高采收率技术的主要手段之一，已经在矿场实践中得到广泛应用［1－3］。聚合物驱过程本身是1个复杂的过程，同时考虑到矿场条件的复杂性，大多数情形下聚合物驱都需要借助于数值方法进行研究［4－7］，聚合物驱数值模拟方法的发展对聚合物驱项目的成功实施至关重要。

近年来，油藏流线模拟技术获得了快速发展，并已经在提高采收率技术预测中得到推广和应用［8－9］。油藏流线模拟具有直观、计算速度快、数值耗散小等优点。Patton等人［4］在1971年就运用流线方法研究了聚合物驱过程，不过在研究过程中忽略了驱替过程中流场的变化，模拟过程中并未对流线进行更新。随着流线模拟方法的发展，流线更新方法逐渐在油藏流线模拟中得到应用［8－9］。Thiele等人［5］于近期将该方法应用到聚合物流线模拟中，同时还运用自适应隐式方法求解了饱和度方程和聚合物浓度方程。

近年来，中国油藏流线模拟技术也获得了快速发展。姚军等人［10］提出了流线数值试井方法;侯建等人［6］结合边界元方法，运用流线方法研究了任意不规则边界情形下聚合物驱替过程。然而，其研究都是基于固定流线的假设下实施的，模拟过程中流线未进行更新;当驱替过程中流体流度差异较大或生产制度发生变化时，固定流线方法会造成较大误差［11］。

本文运用流线方法研究平面聚合物驱过程，计算中考虑了流线更新对模拟结果的影响，通过更新流线来描述驱替过程中的流场的变化;同时，为提高流线方法的精确性，采用了高阶精度差分方法求解饱和度方程和聚合物浓度方程。

1 数学模型

聚合物驱主要通过提高水相黏度、减小驱替过程流度比、提高波及系数等方法，从而提高采收率;驱替过程中还伴有岩石吸附效应、水相渗透率下降、剪切稀化、存在不可及体积等现象。本文采用1种聚合物驱流线模拟方法，考察流线更新对聚合物驱过程的影响，为简单起见，只考虑了聚合物驱过程中黏度变化以及岩石吸附2个因素，其他因素如渗透率下降、剪切稀化等可以在模型中增加相关参数进行研究，具体可以参考文献［5－6］。本文聚合物模型主要基于以下假设。

(1)驱替过程为不可压缩等温达西渗流过程，不考虑重力和毛管力对驱替过程的影响。

(2)油水两相流动，聚合物仅溶于水中，聚合物的存在对水相连续方程没有影响。

(3)不考虑剪切作用对黏度的影响，水相黏度仅仅是聚合物浓度的函数，可以表示为:

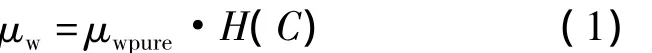
式中:μw为水相黏度，mPa·s;μwpure为纯水黏度，mPa·s;C为聚合物浓度，kg/m3;H(C)为关于聚合物浓度的多项式，可以通过表格输入。

(4)驱替过程中发生等温吸附过程，吸附浓度可以用Langmuir吸附等温线表示［6］:

式中:Ca为吸附浓度，kg/kg;a，b为Langmuir吸附常数，m3/kg。

聚合物驱过程需满足水相连续方程和聚合物浓度连续方程［4－5］。水相连续方程为:

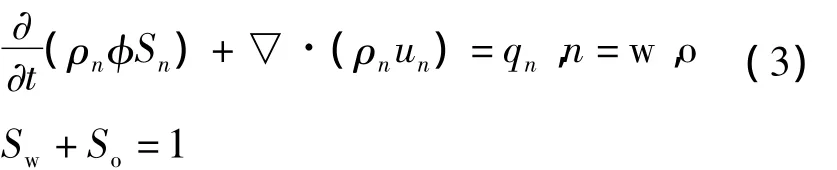
聚合物浓度连续方程为:

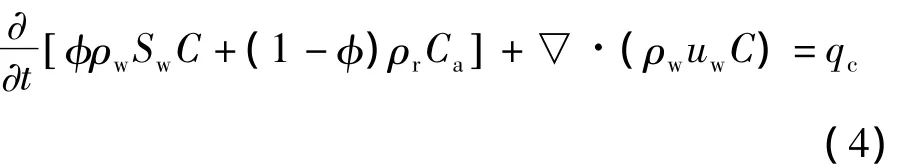
式中:下标n=w，o，分别为水相和油相;S为饱和度;φ为孔隙度;ρ为相密度，kg/m3;ρr为岩石密度，kg/m3;q为源汇项;u为相渗流速度，m/s，满足达西公式:

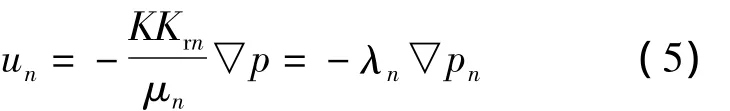
式中:K为地层渗透率，10－3μm2;Kr为相对渗透率;pn为相压力，MPa;不考虑毛管力时，油相和水相压力相等，设p=pw=po。

2 控制方程

定义总速度为ut=uw+uo，由不可压缩流体假设，得到:

油相和水相方程相加消去饱和度，得到聚合物驱过程压力方程为:

式中:λt为总流度，等于油相流度和水相流度之和。

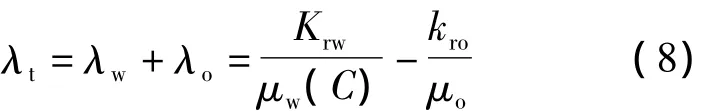
定义流线为s，其切线方向与速度方向一致的曲线［8］，得到:

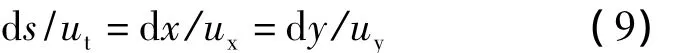
进一步定义沿流线传播时间τ，得到:

利用式(6)得到，水相连续方程和聚合物浓度方程沿流线方向的方程:

式中:fw为水相分流量，fw=λw/(λw+λo)。

根据以上分析表明，流线方法将二维(或三维)饱和度和聚合物浓度方程转换为沿流线一维物质输送方程，降低了求解难度。因此，驱替过程的计算可以先沿流线一维进行，然后汇总各流线结果即可。

3 求解方法

聚合物驱流线模拟过程主要包括:①运用IMPES方法求解压力方程(7);②根据 Pollock方法［10］追踪流线;③为提高计算精度，减小数值耗散，采用显式全变差递减(TVD)差分格式求解饱和度方程(11)和浓度方程(12);④进行流线更新。

4 计算实例

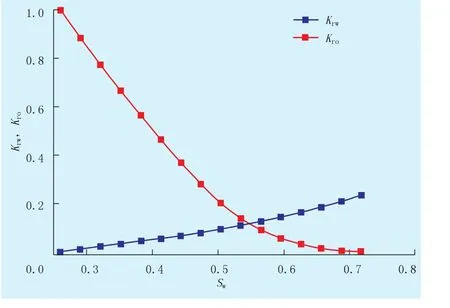
图1 油水相对渗透率曲线

为了分析流线更新及其影响，模拟了平面五点井网聚合物驱过程，并和Eclipse软件进行对比。其中，地质模型参数为:①二维平面均质地层，考虑到对称性，取五点井网的1/4作为研究对象(一注一采情形);②地层渗透率为 300 ×10－3μm2，孔隙度为0.2;③等流量生产，注入和采出流量均为20 m3/d，纯水黏度为1 mPa·s，油相黏度为8 mPa·s;④水相密度为1 000 kg/m3，油相密度为800 kg/m3，岩石密度为2 300 kg/m3。油水两相相对渗透率曲线如图1所示;水相黏度和聚合物吸附浓度随聚合物浓度变化曲线如图2。

图2 聚合物水相黏度变化曲线和吸附曲线

聚合物驱具体实施过程为:注入1.43 PV水后转为聚合物驱，注入浓度为1 kg/m3的聚合物溶液。图3为聚合物驱含水率曲线fw、生产井聚合物采出浓度Cp以及采出程度η随注入孔隙体积的变化关系曲线。约注入2.29 PV时生产井含水率开始下降，且生产井见聚合物;之后逐渐形成含水率曲线“下降漏斗”，含水率约在2.67 PV时降到最小;最终生产井含水率为98%时采出程度约为0.42 PV，而同期水驱采出程度为0.38 PV，采出程度提高了10.5%。其中，图3中还给出了Eclipse软件的计算结果，可以发现两者的结果相近，验证了流线方法的有效性。

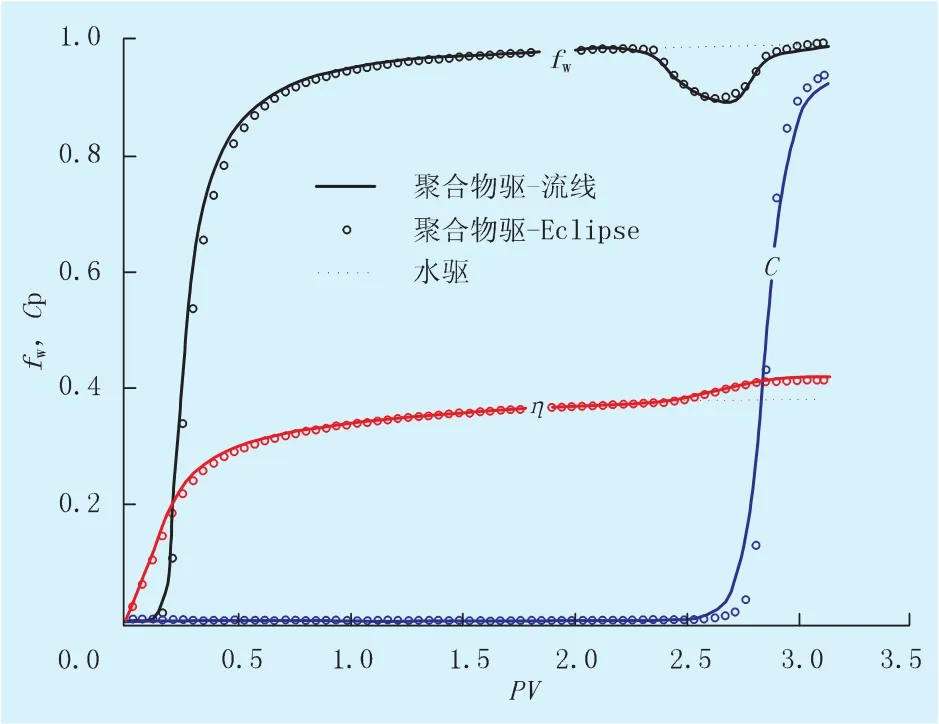
图3 聚合物驱动态曲线

此外，进一步考察了流线更新对聚合物驱流线模拟结果的影响，图4为固定流线和更新流线时聚合物驱模拟结果。可以发现，在水驱阶段，两者吻合较好，固定流线的假设是合理的;然而，转入聚驱阶段后，固定流线方法出现了较大误差，其含水率“下降漏斗”和生产井采出浓度曲线与更新流线方法得到的结果相差较大。正如Martin和Wegner在文献［9］中所指出的:对于不利驱替过程，流度的变化对流场的影响很小，固定流线的假设是合理的;对于有利驱替过程，其流场随着驱替过程的进行变化很大，不更新流线会引起较大的误差。在聚合物驱过程中，前期水驱为不利驱替过程，而转为聚驱后，由于水相黏度的增加，驱替变为有利驱替过程。因此，固定流线方法在水驱阶段的误差较小，而聚驱阶段的误差较大。

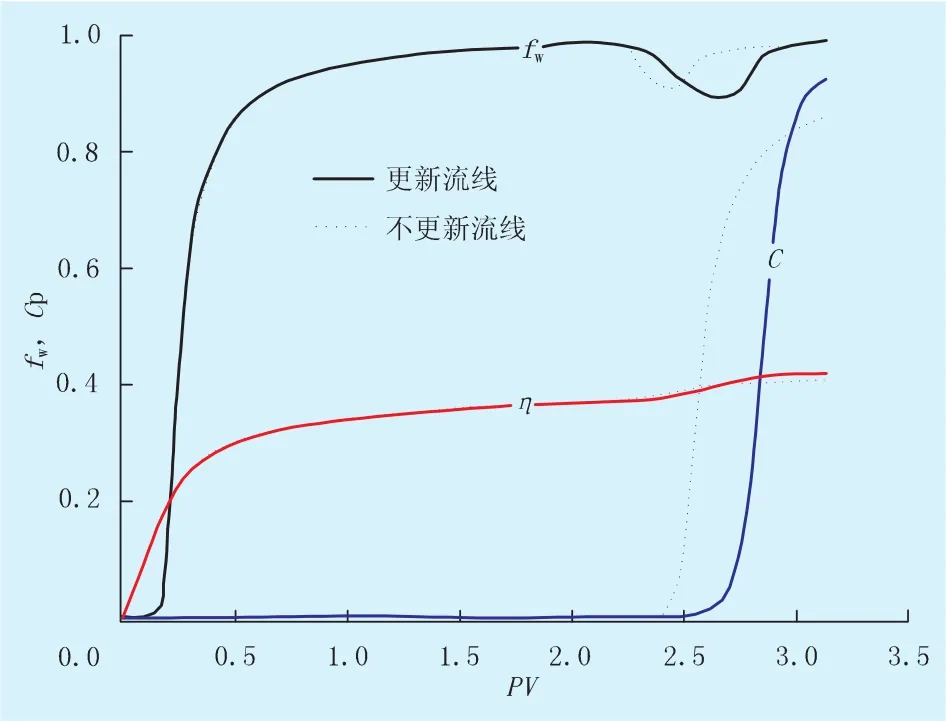
图4 流线更新对聚合物驱流线模拟的影响

5 结论

(1)考虑聚合物驱过程中黏度变化及吸附效应，建立了聚合物驱流线模型。

(2)运用IMPES求解压力方程，并运用Pollock方法追踪流线;饱和度方程和聚合物浓度方程采用了高阶精度显式全变差递减(TVD)差分方法求解，保证了差分方法的精确性。

(3)编写了聚合物驱流线模拟程序，进行了流线更新;预测了五点井网聚合物驱过程，并与商业软件进行了对比，验证了流线更新方法的有效性。

［1］Need ham R B，Peter D H.Polymer flooding review［J］.SPE J，SPE17140，1987:1503 －1507.

［2］王启民，冀宝发，隋军，等.大庆油田三次采油技术的实践与认识［J］.大庆石油地质与开发，2001，20(2):1－8.

［3］刘歆，周凤军，张迎春，等.海上油田稀井网大井距聚合物驱应用与分析［J］.特种油气藏，2011，18(3):104－108.

［4］Patton J T，Coats K H，Colegrove G T.Prediction of polymer flood performance［J］.SPEJ，SPE2546，1971:72 －84.

［5］Thiele M B，Batychy R P，Pollitzer S，et al.Polymer－Flood Modeling using streamlines［C］.SPE115545，2010:313 －322.

［6］侯健，王玉斗，陈月明.聚合物驱数学模型的流线方法求解［J］.水动力学研究与进展，2002，17(3):343－352.

［7］侯健，李振泉，王玉斗，等.考虑扩散和吸附作用的聚合物驱替过程渗流数值模拟［J］.计算物理，2003，20(3):239－244.

［8］姚军，吴明录，胡航.碱聚合物复合驱油藏流线数值试井解释模型及其应用［J］.石油学报，2008，29(6):894－902.

［9］Martin J C，Wegner R E.Numerical solution of multiphase two－dimensional incompressible flow using stream－tube relationships［C］.SPE7140，1979:313 －323.

［10］Pollock D W.Semi－analytical computation of path lines for finite － difference models［J］.Ground Water，1988，26(6):743–750.