临近空间飞行器的滑模变结构解耦控制*

王 鹏 刘鲁华 吴 杰

国防科学技术大学航天与材料工程学院, 长沙 410073

临近空间飞行器(Near-Space Vehicle)是指飞行在临近空间范围的飞行器，临近空间通常指距离地面20～100km的空域[1]。滑翔飞行器是临近空间飞行器的一种，其飞行空域、速度的跨度和变化都非常大，具有快时变、强耦合、强非线性和强不确定的特点，因此，其控制系统的设计更加困难。对这类对象的控制，传统增益预置的线性控制方法难以达到满意的控制效果，还会带来分段过多、控制器频繁切换的问题。近年来，非线性控制方法在临近空间飞行器控制系统设计中被广泛应用，取得了良好控制效果，其中研究较多的非线性控制方法包括动态逆控制[2-4]、滑模变结构控制[5-9]等。

非线性动态逆控制又称为反馈线性化方法，是Senll，Enns等人针对飞机在做大迎角超机动飞行时的本体非线性、强耦合特征而提出来的非线性控制策略[2]，其基本思想是：对于具体的研究对象，用系统模型生成一种可用反馈方法实现的原系统“α阶积分逆系统”，将对象补偿为具有线性传递关系的伪线性系统，实现输入输出解耦。动态逆方法是实现复杂MIMO系统输入输出解耦和反馈线性化的重要方法之一，在高超声速飞行器控制系统设计中被广泛应用。但目前的研究大多针对飞行器的纵向运动模型[3-7]，对完整运动模型的研究较少。本文将针对临近空间飞行器的飞行控制问题，采用完整运动模型开展控制系统设计，从而提高控制系统的适用性。

滑模变结构控制的结构在动态过程中根据系统当前的状态(如偏差及其各阶导数等)有目的地不断变化，迫使系统按照预定“滑动模态”的状态轨迹运动[10]，因此滑模变结构控制对参数偏差和外界干扰具有较强的鲁棒性。设计干扰观测器是滑模控制的一项重要应用[1, 8]，它既可以提高控制系统的性能和工程适用性，又可以消除干扰造成的抖振[11]。基于趋近律设计思想的滑模控制是一种经典而成熟的控制方法，在飞行器控制系统设计中被广泛采用[5-7]，由于简洁的表达形式，使其具有良好的工程适用性。滑模控制方法的主要问题是抖振现象，即状态轨迹到达滑动面后会在滑动面两侧来回穿越，引起控制指令的突变。饱和函数法[5-6]是一种十分有效的抖振抑制方法。本文将动态逆方法实现反馈线性化的能力与滑模控制的强鲁棒性有效结合，设计满足指标要求的六自由度滑模控制系统。

1 飞行器动力学模型

本文研究的滑翔飞行器采用气动舵单一控制方式，其矢量形式动力学模型为

(1)

其中，r为飞行器在惯性坐标系中的位置矢量；mg为引力矢量；R为作用在飞行器上的空气动力矢量，包含了气动舵控制力；J为飞行器的转动惯量；ωT为飞行器相对惯性系的转动角速度；Mst为作用在飞行器上的气动稳定力矩，包含了气动舵控制力矩；Md为飞行器相对大气有转动时的阻尼力矩。

根据高超声速滑翔飞行器的特点，提出下述3个假设条件：

假设1 视地球为均质圆球，忽略地球扁率及切向引力加速度的影响；

假设2 忽略地球旋转的影响，认为ωe=0。此时，发射惯性坐标系与地面坐标系始终重合，不需考虑离心惯性力和哥氏惯性力的作用；

假设3 飞行器的惯量积Jxz=Jyz=0，同时惯量积Jxy为小量，忽略不计。

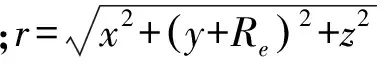
(2)

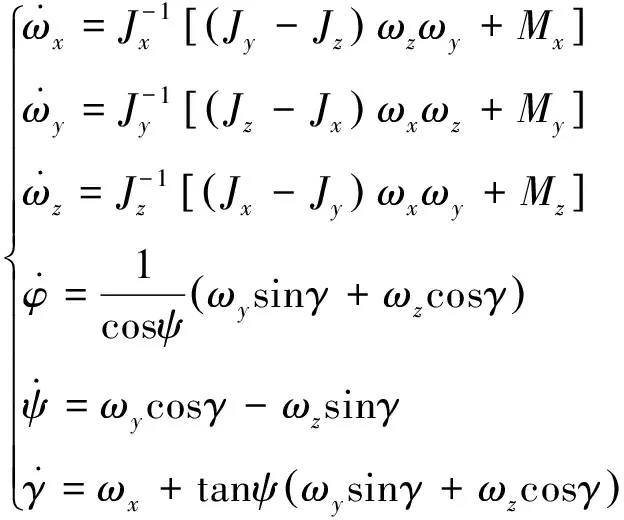
(3)

阻力D、升力L和侧力N的表达式分别为[12]

D=qSCD,L=qSCL,N=qSCN

(4)

其中，q=0.5ρV2为动压；ρ为空气密度；V为飞行器速度；S为飞行器参考面积；CD,CL,CN分别为阻力系数、升力系数和侧力系数。滚动力矩Mx、偏航力矩My和俯仰力矩Mz的表达式分别为[12]

(5)

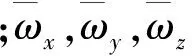
(6)

气动力系数和气动力矩系数为飞行马赫数Ma、高度H、攻角α、侧滑角β及俯仰舵偏角δφ、偏航舵偏角δψ、滚动舵偏角δγ的非线性函数，可表达为如下关系式

(7)

欧拉角之间满足如下关系式

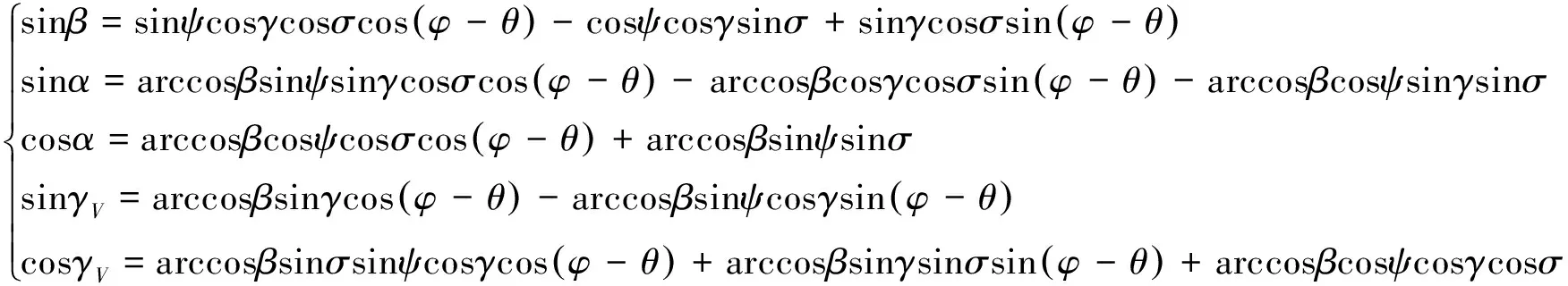
(8)

2 姿态运动模型的反馈线性化

飞行器姿态运动模型的状态变量取为

(9)

(10)

其中，fu(x,u)由式(3)中等号右侧含有控制量的项组成，即含有Mx,My,Mz的项组成；而f(x)由(3)式中其余项组成。

应用动态逆方法对动力学模型进行反馈线性化，需首先分析模型的可逆性。多变量频域理论中MIMO非线性系统的可逆性定理——函数可控性定理如下。

定理1[13]一般MIMO非线性系统在(x0,u0)的邻域内可逆的充分必要条件是在此邻域内存在相对向量阶，即(x0,u0)为Interactor算法的正则点。

由式(3)所示的飞行器姿态运动模型可知，控制量u只包含于气动力矩Mx,My,Mz中，因此判断输出量的导数中是否显含输入量，只需根据导数中是否出现气动力矩进行判断即可。

经过推导可得

(11)

(12)

(13)

由以上分析可知，飞行器姿态运动模型系统的相对阶为k=2+2+2=6，等于系统阶数(n=6)，故飞行器姿态运动模型是可逆的，采用动态逆方法可实现该模型的反馈线性化和解耦控制。

若记式(3)所示的飞行器姿态运动模型构成的非线性系统为原系统∑，即

y=Φ(x,u)

(14)

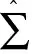
u=Ψ(x,v)

(15)

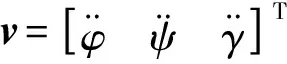
y=Φ[x,Ψ(x,v)]=Γ(x,v)

(16)

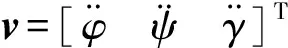
(17)

但这种线性关系仅限于输入输出之间，系统的内部结构可能仍是非线性关系，故将其称为伪线性系统。

图1 姿态运动模型的伪线性复合系统

3 滑模控制系统设计

飞行器姿态运动模型逆系统的输入为俯仰角、偏航角和滚动角的二阶导数，因此为了将滑模变结构控制与动态逆控制结合起来，在控制系统设计时滑模面应包含姿态角的一阶导数。这样，滑动函数仅需计算一次导数，即可含有输入量。为此可取滑动函数为[5]

(18)

式中，λφ,λψ,λγ为严格正常数；eφ=φ-φd，eψ=ψ-ψd，eγ=γ-γd。

为使Sφ,Sψ,Sγ达到0，即使系统轨迹在有限时间内到达滑动面，需为非线性系统选择适当的控制律，满足如下的滑动条件

(19)

根据趋近律设计思想，可以选取如下的等速趋近律

(20)

其中，εφ,εψ,εγ均为可选的正常数；sgn(·)表示符号函数。

对式(18)微分得

(21)

则姿态运动模型逆系统的输入为

(22)

将式(29)带入式(22)得

(23)

为了抑制抖振，将上式中的符号函数sgn(·)用饱和函数sat(·)代替，饱和函数的定义为[6]

(24)

其中，dφ,dψ,dγ为边界层厚度，均为正常数，根据实际情况进行选取。饱和函数的作用是在滑动面附近的一个薄激波层内把控制的不连续性加以平滑，从而抑制抖振现象。于是控制律变为

(25)

基于动态逆的滑模变结构解耦控制系统结构如图2所示。

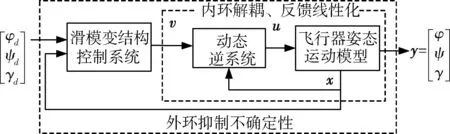
图2 滑模变结构解耦控制系统结构

4 控制系统性能仿真分析

前面设计了基于动态逆的滑模变结构解耦控制系统，下面进行滑翔飞行器姿态运动仿真计算，分析控制系统性能。仿真初始条件如表1所列。

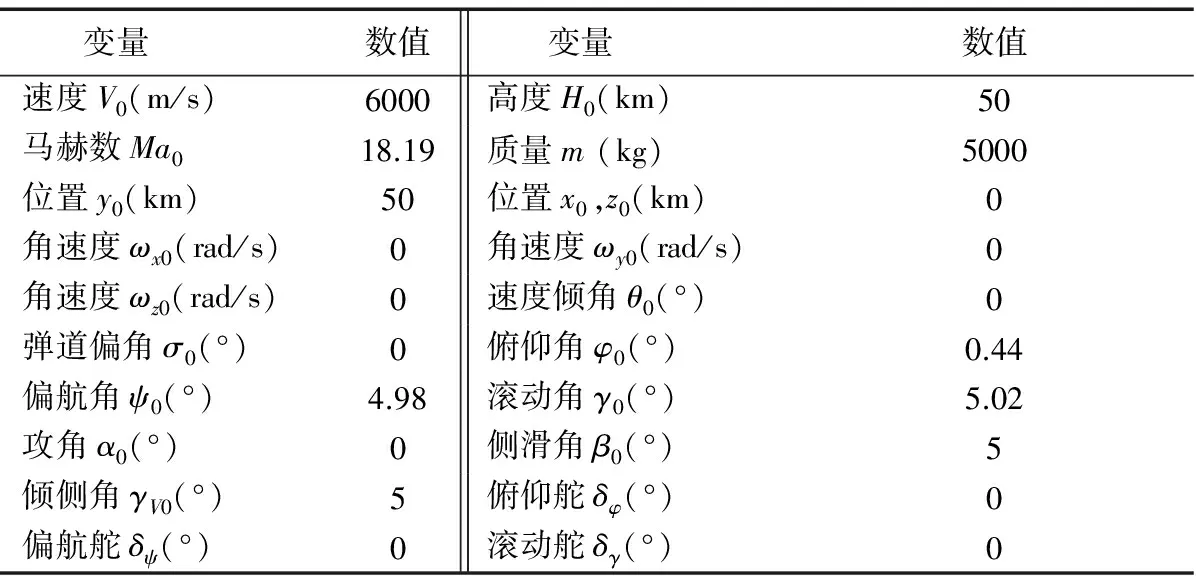
表1 仿真初始条件

本文设计的控制系统的最直接的控制方式为跟踪俯仰角、偏航角和滚动角指令，但由于欧拉角之间可通过式(8)相互计算，因此控制指令可以任意选取3个欧拉角，然后通过实时参数计算得到所需的俯仰角、偏航角和滚动角指令。根据工程应用的一般情况，本文选取攻角、侧滑角和倾侧角作为最终控制目标。仿真中指令值分别取为αd=10°;βd=0°;γVd=0°。滑模控制器参数取为λφ=λψ=λγ=2；εφ=εψ=εγ=25；dφ=dψ=dγ=0.8；仿真步长10ms。

为了更好地考核控制器性能，仿真中采用实际舵模型，即考虑控制舵的指令延迟、偏角超调、幅值限制和角速度限制，其中指令延迟10ms，超调量5%，各通道舵偏角范围为±20°，最大角速度±500(°)/s(即±5(°)/仿真步长)。

滑模控制器的鲁棒性如何，主要看其能否在存在外界干扰和参数偏差的条件下实现对姿态指令的高精度跟踪。下面以是否加入外界干扰、是否考虑参数偏差等构造不同的仿真条件，并给出不同条件下的仿真结果，讨论外界干扰和参数偏差对滑模控制器鲁棒性的影响。三通道干扰模型均为幅值5N·m的正弦干扰。参数偏差模型为

(26)

其中|Δρ|≤0.4,|ΔJ|≤0.1,|Δms|≤0.5,|Δmd|≤0.6。

不同仿真条件下的姿态角控制精度如表2所列。同时存在干扰和参数偏差条件下的仿真结果如图3～5所示。

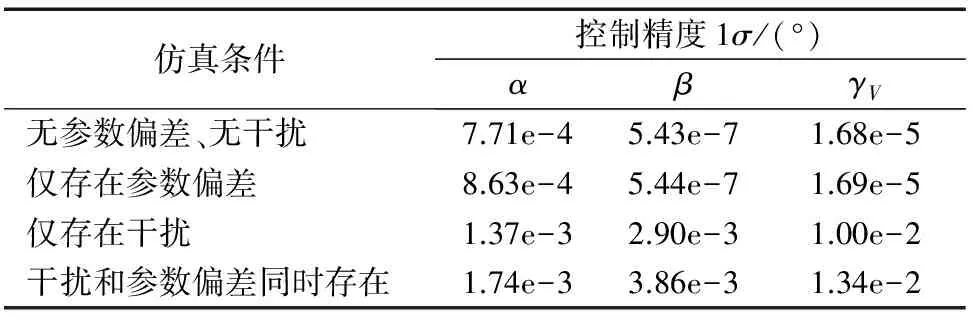
表2 不同仿真条件下的姿态角控制精度

由表2的第1行数据可知，考虑舵机实际工作特性后滑模控制系统仍能保持对攻角、侧滑角和倾侧角的高精度跟踪，说明所设计的控制系统具有工程适用性。由不同条件下的姿态角控制精度对比可知，外界干扰是影响控制系统性能的主要因素，相对而言，参数偏差对控制系统性能影响较小，说明所设计控制系统对参数偏差不敏感。同时考虑外界干扰和参数偏差条件下，控制系统仍具有较高的姿态控制精度，说明所设计控制系统对外界干扰和参数偏差具有较好的鲁棒性。

图3 姿态角

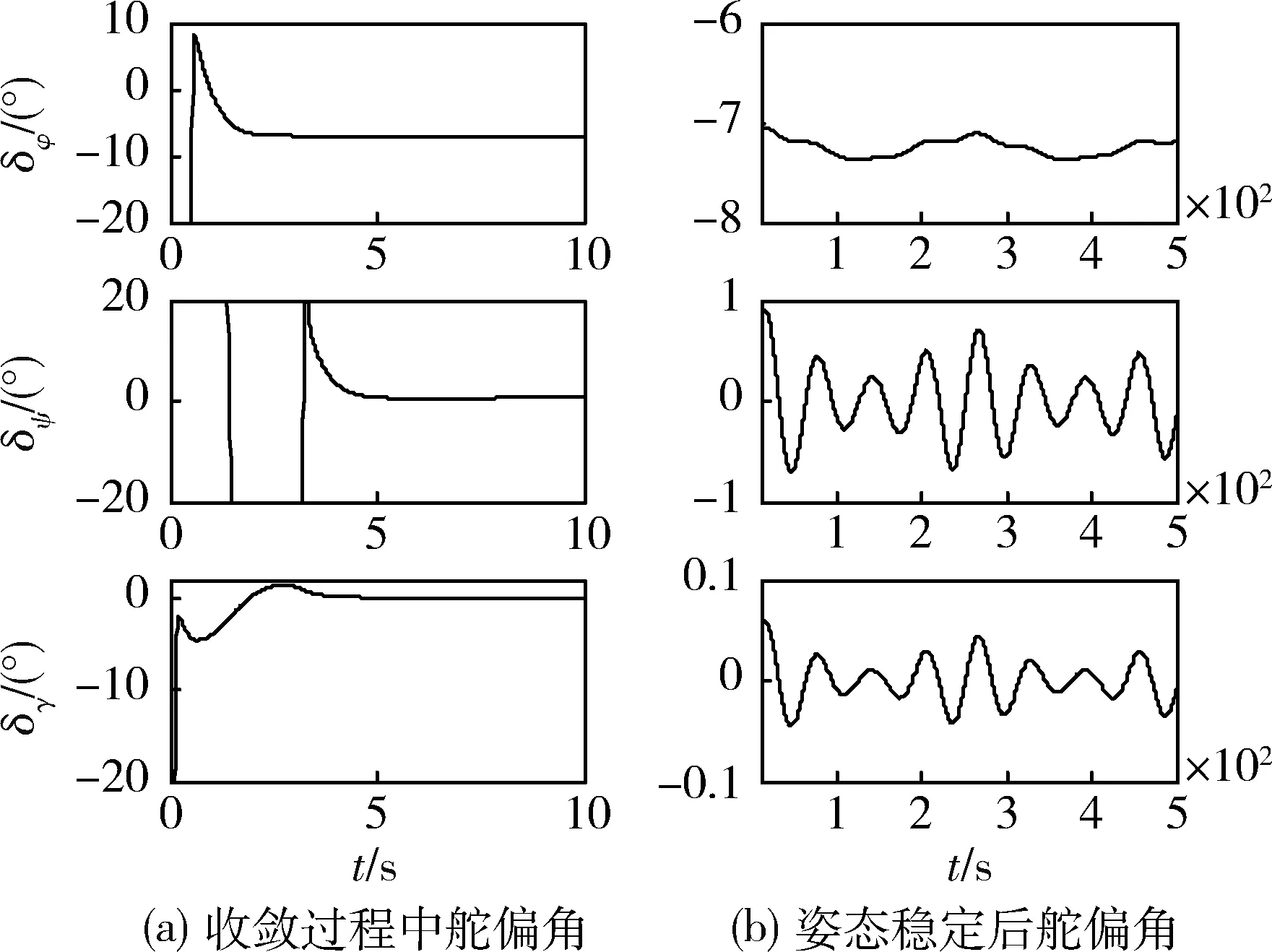
图4 三轴舵偏角

图5 高度、速度变化曲线

由图3可知：同时考虑外界干扰、参数偏差及存在较大姿态初始误差的条件下，控制系统仍能快速跟踪姿态指令值，并且稳态时，误差波动在|α-αd|<0.004°，|β-βd|<0.01°，|γV-γVc|<0.03°的边界范围内，说明所设计的滑模控制系统具有较好的控制性能，对外界干扰和参数偏差具有较强的鲁棒性。

由图4所示的结果可知：三轴等效舵转角幅值在允许的范围内，平稳变化，未出现明显的抖振现象，饱和函数的作用得到充分发挥。由于舵机指令延迟、偏角超调和角速度限制等实际工作特性，同时受到参数偏差和外界干扰的影响，舵偏角在小范围内波动。

5 结论

应用MIMO非线性系统的可逆性定理证明了临近空间飞行器姿态运动模型是可逆的。采用动态逆方法可实现该模型的反馈线性化和解耦控制。虽然系统的内部结构可能仍是非线性关系，但伪线性系统的输入输出之间具有线性传递关系，理论上可将该线性关系简单地表示成线性积分解耦型传递函数。

在考虑舵机实际工作特性、参数偏差和外界干扰的条件下，滑模控制系统可以保持对攻角、侧滑角和倾侧角的高精度跟踪，说明所设计的控制系统对外界干扰和参数偏差具有鲁棒性，可以满足实际飞行的要求，具有较好的工程适用性。

参 考 文 献

[1] 程路, 姜长生, 都延丽, 等.基于滑模干扰观测器的近空间飞行器非线性广义预测控制[J].宇航学报, 2010, 31(2): 423-431. (Cheng Lu, Jiang Changsheng, Dou Yanli, et al. The Research of SMDO based NGPC Method for NSV Control System[J]. Journal of Astronautics, 2010, 31(2): 423-431.)

[2] Snell S A, Enns D F and Garrard L. Nolinear Inversion Flight Control for a Supermameuverable Aircraft[J]. Jorunal of Guidance, Control, and Dynamics, 1992, 15(4): 976-984.

[3] Wang Q, Stengel R F. Robust Nonlinear Control of a Hypersonic Aircraft[J]. Journal of Guidance, Control, and Dynamics, 2000, 23(4): 577-585.

[4] XU Haojian, Mirmirani M and Ioannou P A. Robust Neural Adaptive Control of a Hypersonic Aircraft[C]. AIAA Guidance, Navigation and Control Conference and Exhibit, 2003, AIAA 2003-5641.

[5] XU Haojian, Mirmirani M D, Ioannou P A. Adaptive Sliding Mode Control Design for a Hypersonic Flight Vehicle[J]. Journal of Guidance, Control and Dynamics, 2004, 27(5): 829-838.

[6] 刘燕斌, 陆宇平. 基于变结构理论的高超音速飞机纵向逆飞行控制[J]. 信息与控制, 2006, 35(3): 388-392. (Liu Yanbin, Lu Yuping. Longitudinal Inversion Flight Control Based on Variable Structure Theory for Hypersonic Vehicle[J]. Information and Control, 2006, 35(3): 388-392.)

[7] LI Huifeng, SUN Wenchong, LI Zhaoying, XUE Songbai. Index Approach Law Based Sliding Control for a Hypersonic Aircraft[C]. U.S. Air Force T&E Days, Albuquerque, New Mexico, 2009. AIAA 2009-1734.

[8] 刘强, 于达仁, 王仲奇. 高超声速飞行器的滑模观测器设计[J]. 航空学报, 2004, 25(6): 588-592. (Liu Qiang, Yu Daren, Wang Zhongqi. Sliding-Mode Observer Design for a Hypersonic Vehicle[J]. Acta Aeronautica Et Astronautica Sinica, 2004, 25(6): 588-592.)

[9] Keum W Lee, Subramanian Ramasamy and Sahjendra N Singh. Adaptive Sliding Mode 3-D Trajectory Control of F/A-18 Model via SDU Decomposition[C]. AIAA Guidance, Navigation and Control Conference and Exhibit, Honolulu, Hawaii, 2008, AIAA 2008-6460.

[10] 赵文杰, 刘吉臻, 弓学敏. 不确定非线性系统变结构控制的研究[J]. 华北电力大学学报, 2005, 32(5): 22-26. (Zhao Wenjie, Liu Jizhen, Gong Xuemin. Research Status of Variable Structure Control for Uncertain Nonlinear Systems[J]. Journal of North China Electric Power University, 2005, 32(5): 22-26.)

[11] 刘金琨, 孙富春. 滑模变结构控制理论及其算法研究与进展[J]. 控制理论与应用, 2007, 24(3): 407-418. (Liu Jinkun, Sun Fuchun. Research and Development on Theory and Algorithms of Sliding Mode Control[J]. Control Theory & Applications, 2007, 24(3): 407- 418.)

[12] 赵汉元. 飞行器再入动力学和制导[M]. 长沙: 国防科技大学出版社, 1997. (Zhao Hanyuan. Dynamics and Guidance for Reentry Vehicle[M]. Changsha: National University of Defense Technology Press, 1997.)

[13] 戴先中. 多变量非线性系统的神经网络逆控制方法[M]. 北京: 科学出版社, 2005. (Dai Xianzhong. Neural Network Inverse Control Method for Multivariable Nonlinear System[M]. Beijing: Science Press, 2005.)