卫星姿态系统执行器故障的自适应控制设计*

蔡 超 姚雪莲 齐瑞云

1.南京航空航天大学自动化学院，南京 210016 2.北京航空航天大学自动化科学与电气工程学院，北京 100191

卫星是由功能各异的单机子系统组成的一个大系统，而姿态控制系统是其中复杂且故障多发的子系统，调查显示[1]姿态控制系统故障占卫星所有故障的30%以上，而由于转动部件的存在，作为卫星主要执行器的飞轮是姿态控制系统中故障高发的部件之一。另一方面，卫星往往存在冗余执行器，因此合理利用冗余执行器进行故障补偿就十分必要。

当前航天器正向自主运行的方向发展，其目标是提高航天器在难以预料和多变环境下的自主运行能力[2],这要求控制系统在快速精确应对各种姿态指令时还要考虑各种故障与条件限制，如建模不确定性、外部干扰、子系统故障及资源的限制等，于是新的理论和方法不断被提出，以期在不同条件下获得更理想的控制性能。目前国内外各种文献在航天器姿态控制方面已有丰硕研究成果，如非线性反馈控制[3]，最优控制[4-5]，神经网络[6]，滑模控制[7]，自适应控制[8-9]及鲁棒控制[10]等。对卫星这样的复杂系统而言，实际运行过程中执行器故障发生时间、故障值大小以及故障模式是不确定的，而自适应控制可以有效解决故障的不确定性问题。例如文献[11] 提出了一种基于自适应观测器的故障诊断方法，该方法能有效地估计单飞轮故障的大小。文献[12]提出了一种基于自适应快速终端滑模控制的容错控制方法，与传统的滑模控制相比，该方法通过对自适应算法的运用，在保证系统鲁棒性和可靠性的同时，具有更快的收敛速率。目前对包括卫星在内的许多安全性要求较高的系统而言，在缺乏故障先验知识的情况下，采用自适应方法往往能获得令人满意的控制效果。

本文针对带冗余执行器的卫星姿态控制系统，考虑部分执行器故障且故障不确定的情况，将执行器故障参数化。先设计故障已知情况下的控制方案，再结合Backstepping方法及Lyapunov稳定性定理得到参数自适应律及容错控制器的具体形式，从而调整正常执行器的输入，补偿故障执行器的影响，使得当一个甚至多个执行器故障，且故障不确定的情况下，闭环系统稳定且输出信号能渐进跟踪参考输出信号。

1 问题描述

常用欧拉角方程描述卫星姿态，可得到以飞轮为主要执行器的卫星运动学和动力学方程如下[13-14]：

(1)

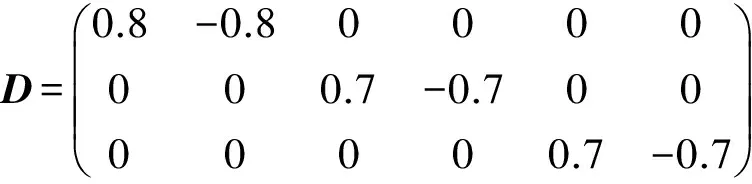
(2)

(3)

y=x1

(4)

本文考虑的卫星有6个执行器，这6个执行器对称分布于卫星体坐标系的3个轴，且推力垂直于对应的坐标轴，此时飞轮位置分布矩阵能简单地由执行器和卫星质心间的距离决定，如图1所示[15]，6个执行器每2个为一组，其中一个坏了，另一个可以补偿，但不允许同一组的2个执行器同时发生故障。

图1 卫星6个飞轮的分布示意图

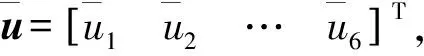
(5)

则可将故障信号表示为[9]：

(6)

当执行器发生故障时，卫星主体的输入信号u(t)可以表示为：

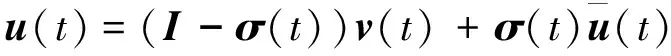
(7)

式中，对角矩阵σ=diag{σ1(t)，σ2(t)，…，σ6(t)}是卫星执行器故障模式矩阵，第i个执行器故障时，σi=1，否则σi=0。系统的基本结构如图2所示。

图2 系统基本结构框图

考虑如下4种情况，其他故障情况可类似处理：

1) 执行器无故障，即：

ui=vi,i=1,2,…,6,0≤t≤ti；

2) 某个控制通道的执行器坏了1个，取执行器1故障，即：

ui=vi,i=2,3,…,6,0≤t≤ti；

3)某2个通道的执行器各坏了1个，取执行器1和3故障，即：

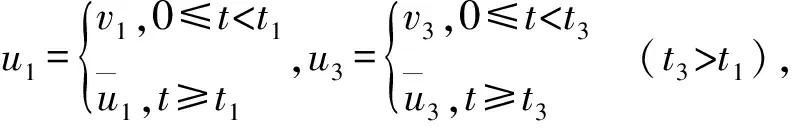
4)3个通道的执行器各坏了1个，取执行器1，3和5故障，即：

本文的控制目标是针对卫星控制系统执行器发生未知故障情况下的姿态跟踪控制问题，设计自适应反馈控制信号v(t)，使得：

1)闭环系统稳定；

2)实现输出y对参考输出ym的渐近跟踪。

2 自适应执行器故障补偿设计

下面先进行标称故障补偿设计，即假设故障信息(故障值和故障模式)已知情况下的设计，再结合Backstepping方法设计自适应控制方案，以补偿不确定的执行器故障。

2.1 标称故障补偿设计

为简化问题，先假设故障已知，针对4种情况，设计4个独立的补偿方案。

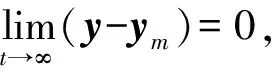
wd=g2u

(8)

1)无故障时的标称故障补偿设计。此时u=v,t≥0，控制信号方程为wd=g2v，设：

(9)

(10)

(11)

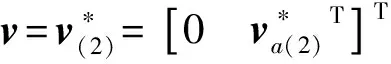
(12)

则此时控制信号方程为：

(13)

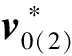
(14)

记：

(15)

则此时控制信号方程为：

(16)

(17)

(18)

则此时控制信号方程为：

(19)

(20)

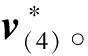
5)参数已知情况下的综合设计。引入如下形式的指示函数：

(21)

综合各单独情况的设计结果，可得标称控制器如下：

(22)

2.2 自适应故障补偿设计

因为实际上指示函数和故障信号未知，故式(22)中标称控制信号v*无法使用，为了解决故障的不确定性问题，需要设计自适应故障补偿控制器v(t)。

2.2.1 自适应控制器

由式(22)可以得到自适应控制器的结构为：

v(t)=χ1v(1)+χ2v(2)+χ3v(3)+χ4v(4)

(23)

(24)

执行器1故障时，由式(12)～ (14)有：

(25)

则：

(26)

执行器1和3故障时，由式(15)～ (17)有：

(27)

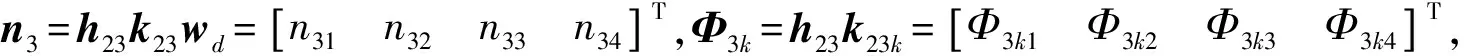
(28)

执行器1，3和5故障时，由式(21)～(23)有：

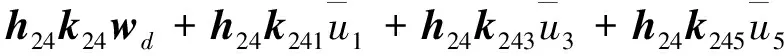
(30)

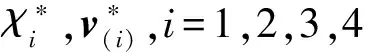
(31)

2.2.2 Backstepping控制设计

为得到参数自适应律，还要计算故障不确定引起的控制信号方程wd与实际w的误差，通过利用Backstepping方法[16]求解wd，又由式(7)，有：

w-wd=g2(I-σ)(v-v*)

(32)

而w可以由w-wd和wd相加得到，最后将w-wd转化为v-v*，对v-v*设计自适应律更新控制器参数，就可以解决故障不确定引起的误差。

引入z1=x1-ym，z2=x2-α1，取虚拟控制变量α1为：

(33)

有：

(34)

(35)

并且可以得到：

(36)

式中，c1>0，c2>0为常数，可适当选取。而由式(24)～(31)，可以得到：

(37)

2.2.3 自适应律设计

设无故障时的Lyapunov函数如下：

(38)

执行器1故障时的Lyapunov函数如下：

(39)

执行器1和3故障时的Lyapunov函数如下：

(40)

执行器1，3和5故障时的Lyapunov函数如下：

(41)

令它们对时间的一阶导数为：

(42)

经过综合计算，可以得到：

(43)

(44)

(45)

(46)

(47)

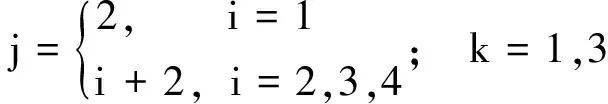
(48)

k=1,3,5

(49)

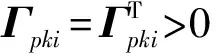
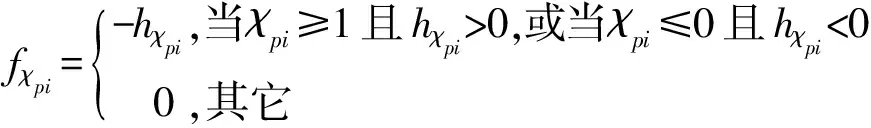
(p=1,2,3,4)，

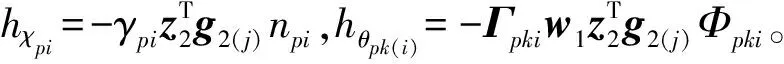
由θ1(t)，θ3(t)和θ5(t)的物理意义，有：

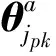
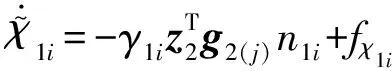
3 仿真结果

本节将对上文的故障补偿方案进行仿真验证。

3.1 仿真条件

卫星姿态控制模型如式(1)所示，其状态空间方程如式(2)～(4)所示，据此模型进行仿真，仿真过程中，主要通过观察输出y1(t)能否对参考输出ym(t)实现渐近跟踪来验证方案的有效性。根据实际姿态控制应用及卫星的特性，仿真中取参考输出信号为：

然后在以下条件下进行仿真研究：

1)无故障，即所有的执行器正常工作：

ui=vi,i=1,2,…,6,t<50s；

2)执行器1卡死(表现为常值故障)：

u1=0.5N·m,ui=vi,i=2,3,…,6,50s≤t<100s；

3)执行器1和3发生常值故障：

u1=0.5N·m,u3=0.5N·m,ui=vi,i=2,4,5,6,100s≤t<150s；

4)执行器1和5发生常值故障，执行器3摩擦力矩增大：u1=0.5N·m,u3=[0.5-0.01(t-150)]N·m,u5=0.5N·m，ui=vi,i=2,4,6,150s≤t<200s。

3.2 仿真结果

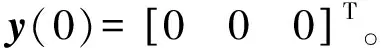
图3 输出信号(卫星的姿态角)

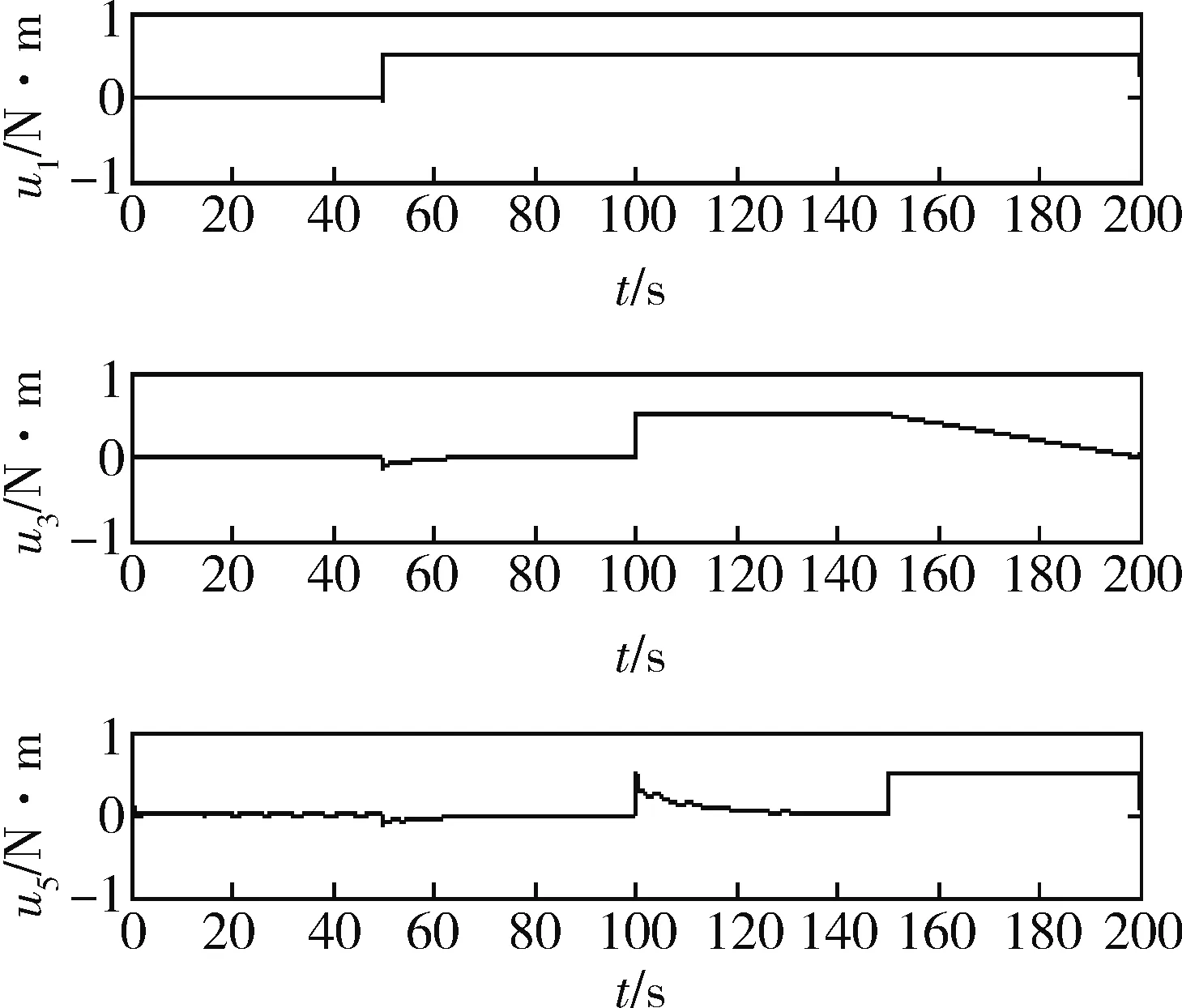
图5 输入信号u1，u3和u5

图6 输入信号u2，u4和u6

由图3～4可以看出在执行器发生故障的瞬间(即50s，100s和150s处)，输出信号和跟踪误差信号都出现震荡响应，且都随时间最终稳定，这在当执行器1，3和5同时故障时表现更为明显，表明故障确实得到了补偿，输出信号稳定且能对参考输出信号实现渐近跟踪。

由图5可以看出输入信号u1，u3和u5与故障情况的对应关系，当t<50s时没有执行器发生故障；当t≥50s时，执行器1卡死；当100s≤t≤150s时，执行器3卡死；当t≥150s时，执行器5发生常值故障，执行器3摩擦力矩增大。

图6则显示了输入信号u2，u4和u6的变化情况，可以看出当一个执行器发生故障时，不论故障为常值故障还是时变故障，其他执行器的输入信号同时出现震荡响应，其中，与故障执行器同一组的冗余执行器(如u2为与u1同组的冗余执行器)的输入信号变化体现了同组执行器间的故障补偿。

另外，当执行器故障时，由自适应参数在线调整的特点可知，控制器参数χpi，θpk(i)(图中没有表示出来)的值也随着时间变化。当执行器发生时变故障时，该方案也可以获得理想的性能。

系统中的所有信号都有界，系统各信号的响应符合预期，闭环系统稳定输出能对参考输出渐近跟踪，该自适应执行器故障补偿方案满足控制目标。

4 结论

卫星因为造价及发射成本很高，所以对系统的安全性及可靠性要求很高。本文针对带有冗余执行器的卫星姿态控制系统，利用控制信号方程，结合Backstepping方法，应用自适应思想，将未知执行器故障参数化，并据此引入了故障模式和故障值的自适应律，设计了一个容错自适应执行器故障补偿方案。该控制方案实现了在卫星出现一个甚至多个执行器故障，且故障不确定的情况下，系统能通过调整正常执行器的控制输入，补偿故障执行器对系统的影响，保证闭环系统的稳定性以及输出信号对参考输出信号的渐近跟踪。对该卫星姿态系统的自适应容错控制方案的仿真结果证明了该方案可以获得理想的故障补偿性能。

参 考 文 献

[1] Tafazoli M. A Study of On-Orbit Spacecraft Failures[C]. Proceedings of 58th International Astronautical Congress， Hyderadbad: IAF/IAA, 2007: 6297-6307.

[2] 邢琰，吴宏鑫，王晓磊，等. 航天器故障诊断与容错控制技术综述[J]. 宇航学报， 2003,24(3):221-226.(XING Yan, WU Hongxin ,WANG Xiaolei, et al. Survey of Fault Diagnosis and Fault-Tolerance Control Technology for Spacecraft[J].Journal of Astronautics, 2003,24(3):221-226.)

[3] Xing G Q, Parvez S A. Nonlinear Attitude State Tracking Control for Spacecraft[J].Journal of Guidance, Control, and Dynamics, 2001, 24(3): 624-626.

[4] Luo W, Chu Y C, Ling K V. Inverse Optimal Adaptive Control for Attitude Tracking of Spacecraft[J].IEEE Transactions on Automatic Control, 2005, 50(11): 1639-1654.

[5] 陈雪芹，耿云海，王峰，等.卫星姿态容错控制系统的鲁棒自适应逆最优控制[J]. 中国空间科学技术,2008，(2):35-41.(CHEN Xueqin, GENG Yunhai,WANG Feng, et al. Satellite Attitude Fault-tolerant Control Based on Robust Adaptive Inverse Optimal Control[J]. Chinese Space Science and Technology, 2008 (2):35-41.)

[6] 李爱军，倪晓彬，王伟，等.再入航天器的神经网络自适应控制[J]. 航天控制,2004，22(3):31-34.(LI Aijun, NI Xiaobin, WANG Wei, et al. Neural Network Adaptive Control for Re-entry Vehicle[J].Aerospace Control, 2004,22(3):31-34.

[7] 程月华，姜斌，孙俊，等.基于滑模观测器的卫星姿态控制系统滑模容错控制[J].上海交通大学学报,2011,45 (2):190-201.(CHENG Yuehua, JIANG Bin, SUN Jun, et al. Sliding Mode Fault Tolerant Control for Satellite Attitude Systems Based on Sliding Mode Observer[J].Journal of Shanghai Jiaotong University, 2011,45 (2):190-201.)

[8] X Yao, G Tao, R Qi. An Adaptive Actuator Failure Compensation Scheme for Spacecraft[C]. Chinese Control Conference, Hefei, China, July, 2012 .

[9] X Yao, G Tao, R Qi, B Jiang. An Adaptive Actuator Failure Compensation Scheme for an Attitude Dynamic Model of Near Space Vehicles[C]. American Control Conference, Montréal, Canada, Jun,2012.

[10] 管宇.卫星姿态控制系统的鲁棒容错控制研究[D]. 哈尔滨：哈尔滨工业大学，2006.(GUAN Yu.Research on Satellite Attitude Control System Based on Robust Fault-Tolerant Control[D]. Harbin: Harbin Institute of Technology, 2006.)

[11] 王小丽，倪茂林.基于自适应观测器的非线性系统故障诊断[J]. 空间控制技术与应用, 2008,34 (4):33-37.(WANG Xiaoli, NI Maolin.An Adaptive Observer Based Fault Diagnosis for Nonlinear Systems[J]. Aerospace Control and Application, 2008,34 (4):33-37.)

[12] 赵琳，闫鑫，郝勇，等. 基于快速终端滑模的航天器自适应容错控制[J].宇航学报, 2012,33 (4):426-435.(ZHAO Lin, YAN Xin, HAO Yong, et al. Adaptive Fault Tolerant Control for Spacecraft Based on Fast Terminal Sliding Mode[J].Journal of Astronautics, 2012,33 (4):426-435.)

[13] Zhou D, Shen T, Tamura K. Nonlinear and Adaptive Nonlinear Controllers for Attitude Stabilization and Tracking of a Spacecraft[J]. Transactions of the Japan Society for Aeronautical and Space Sciences, 2005, 48(159): 7-12.

[14] M J Sidi. Spacecraft Dynamics and Control[M]. England: Cambridge Univ.Press,1997:96-108.

[15] Cai W, Liao X, Song D Y. Indirect Robust Adaptive Fault-tolerant Control for Attitude Ttracking of Spacecraft[J].Journal of Guidance, Control, and Dynamics, 2008, 31(5): 1456-1463.