样本数据归一化对GPS高程转化结果的影响分析
2013-05-15罗玉彬牛冉雯
罗玉彬,牛冉雯
(河南省地质矿产勘查开发局,河南郑州450001)
一、引 言
GPS测量技术在工程测量中的地位日益重要。特别是在具有跨越区域长、沿线地形变化复杂等特点的工程中的应用,显示出了常规测量无可比拟的优越性,大大减轻了劳动强度,提高了工作效率和测量精度[1-2]。GPS测量系统的测高数据为大地高H,即点到WGS-84椭球表面的距离。而在公路测量中,地面点的高程采用正常高系统,地面点的正常高Hr即地面点沿铅垂线至似大地水准面的距离。H和Hr之间存在一个高程异常差值。由于GPS定位技术只解决了平面位置问题,而不能以工程要求的精度将GPS大地高转换为正常高,严重影响了GPS三维定位的应用发展,使其提供三维坐标的优越性未能得到充分发挥[3]。
GPS高程转换方法有很多,利用神经网络的方法就是其中一种,它根据GPS水准数据进行GPS高程转换时,样本数据的归一化是必不可少的过程。不少文献专门针对基于神经网络的GPS高程转换作了深入研究,但只是从建模方法上对神经网络方法进行了研究[4-8],而并没有详细地讨论在建模的过程中样本数据的归一化方式对神经网络方法的影响。
二、基本理论与方法
样本数据归一化是指通过选定的归一化方法将神经网络的输入、输出数据限制在一定范围内。本文中,笔者将点的横坐标、纵坐标和正常高作为样本数据,对于该样本数据来说,点的纵、横坐标值
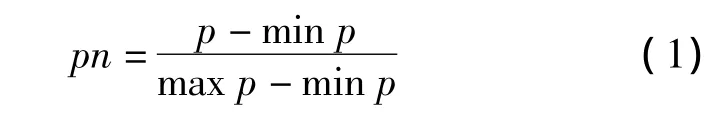
式中,p为需要进行归一化处理的数据;pn为归一化后的样本数据;min p为p中的最小值;max p为p中的最大值。该方法归一化后,样本数据的范围是[0,1]。由于[0,1]的归一化方法,可能导致区间中一点(有时是区间中点)附近样本过于集中,该点附近某点存在大扰动时,都可能导致网络瘫痪,网络的整体误差难以下降。因此将归一化方法适当调整,即将样本数据通过线性变换转换到区间[a,b],使数据在区间内分布更合理,以满足训练的需要。于是本文提出了值域为[-1,1]的归一化方法(归一化函数B),即与正常高值相差悬殊,为了使网络训练一开始就给各输入分量以同等重要的地位,因此必须将输入数据变换到同一范围中[9]。目前,在GPS高程转换过程中,常用的数据归一化方法(归一化函数A)为
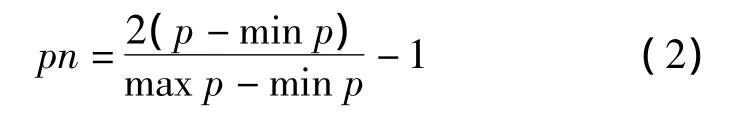
式中,p为需要进行归一化处理的数据;pn为归一化后的样本数据;min p为p中的最小值;max p为p中的最大值。该方法归一化后,样本数据的范围是[-1,1]。
三、实例分析
1.实例概况
实测数据为某地公路控制测量数据。点位分布如图1所示。其中,A、B、C、D为测量区域的4个边界点;黑点为测量点的平面位置;1,2,…,28为点的序号(点名)。由三等水准测量获得各点的正常高,同时获得各点的GPS大地高,从而得到这些点的高程异常值。运用神经网络模型进行GPS高程转换时,将同时具有已知高程数据和GPS测量数据的控制点数据作为学习集,将只有GPS测量数据的控制点数据作为工作集,并将待求点的高程异常作为神经模型的输出值。
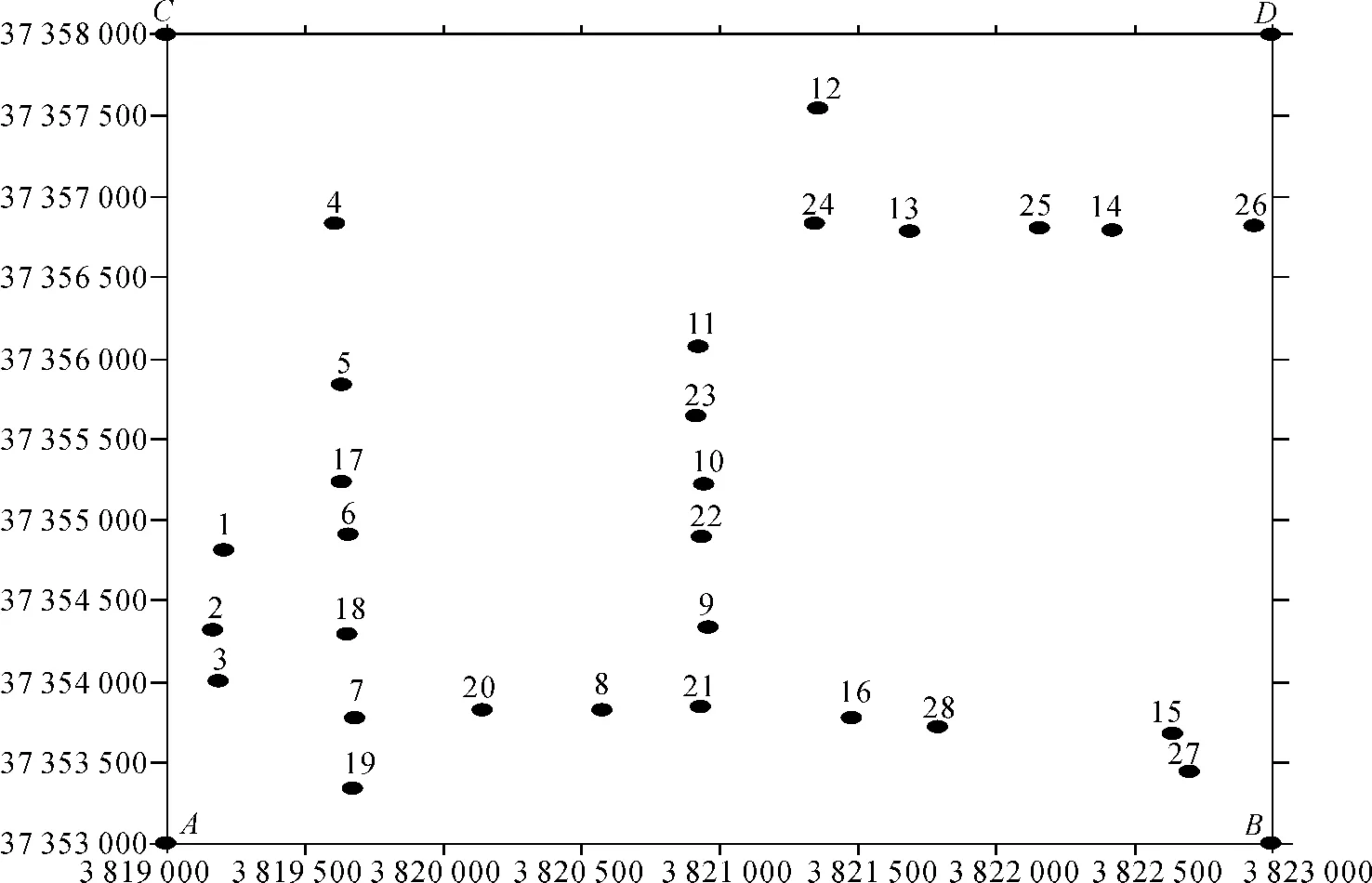
图1 某地公路控制测量数据点的平面分布
2.基于反向传播(BP)神经网络的转换GPS高程
将图1中1—16号点的纵坐标(X)、横 坐 标(Y)、WGS-84高程(H)、高程异常(ε)通过归一化之后的数据作为学习样本,训练X、Y、H与ε之间的关系函数;用17—28号点的X、Y、H的归一化值作为工作数据,计算这些点的高程异常的归一化值,通过归一化公式反算出这些点的高程异常(ε'),进而算出这些点的GPS转换正常高,并与17—28号点的已知高程异常进行比较。结果见表1,表2和图2。
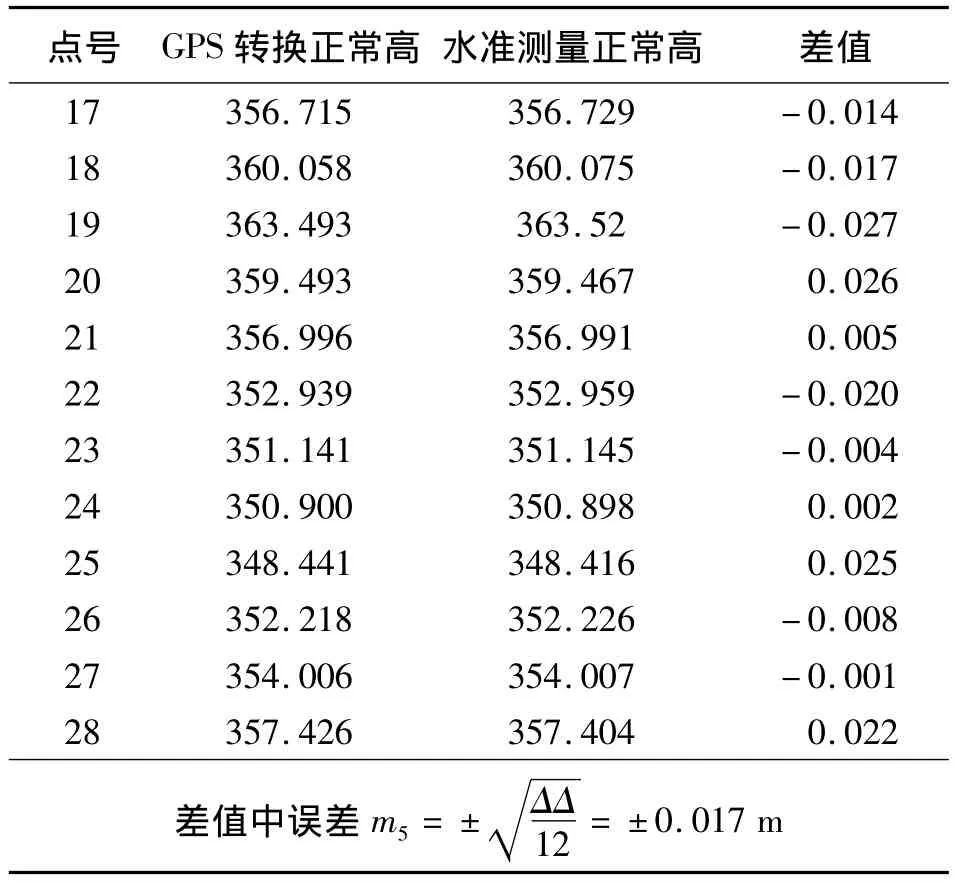
表1 按函数A归一化后的GRNN转换计算结果 m
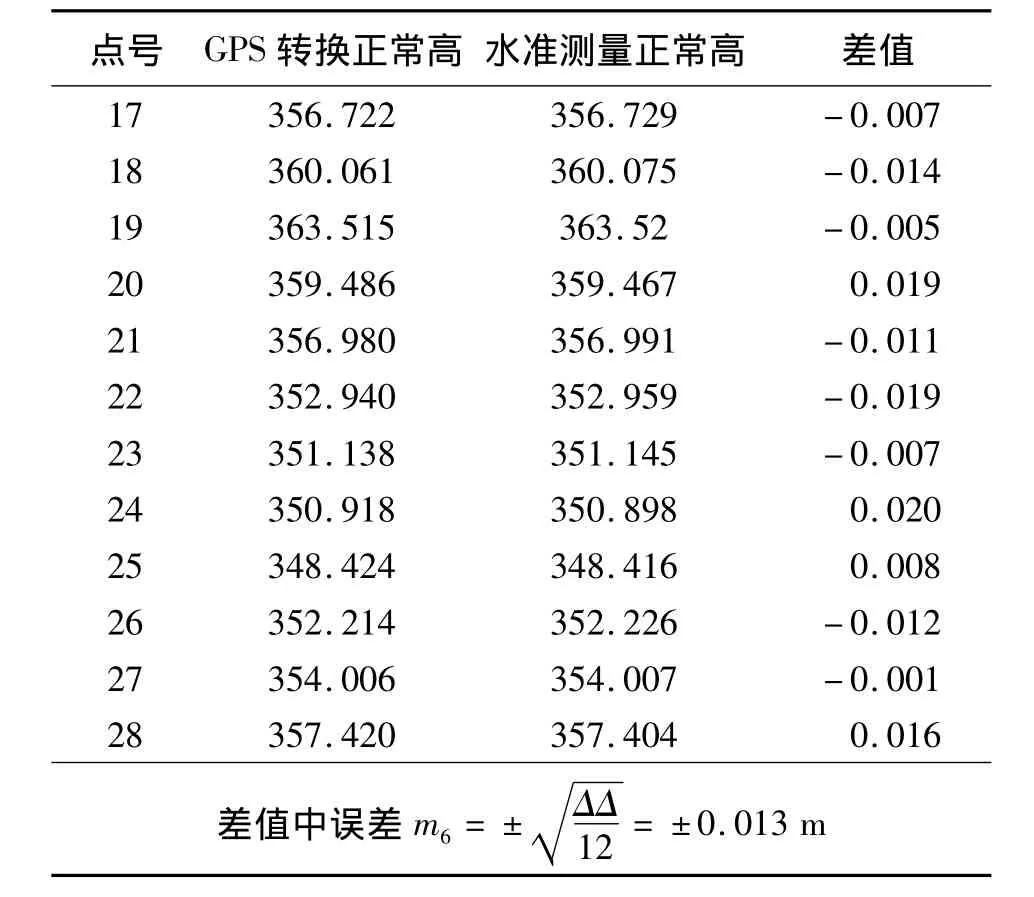
表2 按函数B归一化后的GRNN转换计算结果 m
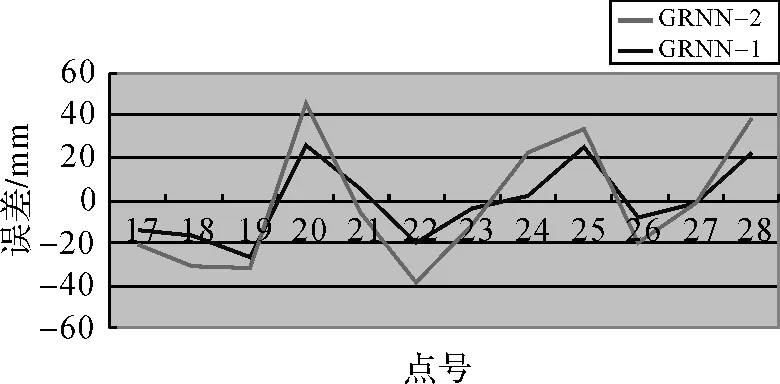
图2 基于GRNN转换计算GPS拟合正常高与水准测量正常高的差值曲线
图2中,GRNN-1为按函数A归一化后的GRNN转换;GRNN-2为按函数B归一化后的GRNN转换。从图2可以看出,在中误差方面GRNN-2转换结果出现正负误差次数相差不多,且差值最大值为20 mm,更接近于正态分布。
综合比较表1、表2中GPS拟合正常高与水准测量正常高的差值中误差和图2中误差曲线可以得出,采用函数B归一化后的GRNN算法计算出的GPS转换正常高最接近于水准测量正常高,方法最优。
四、结束语
本文以样本数据预处理方式对基于神经网络的GPS高程转换的影响为切入点,探讨了不同数据预处理方法对转换结果的影响,在数据预处理中弥补了前人研究只从建模方法上优选模型的做法。本文提出的值域为[-1,1]的归一化函数(函数B)优于传统的值域为[0,1]的归一化函数(函数A)。
[1] 刘基余,李征航,王跃虎,等.全球定位系统原理及其应用[M].北京:测绘出版社,1993.
[2] 刘大杰,施一民,过静珺.全球定位系统 (GPS)的原理与数据处理[M].上海:同济大学出版社,1996.
[3] 肖远平.GPS高程拟合及其在公路勘察中的应用研究[D].长沙:中南大学,2009
[4] 高宁,高彩云,吴良才.关于BP神经网络转换GPS高程的若干问题[J].测绘工程,2006,15(3):67-69.
[5] 胡伍生,华锡生,吴中如.用神经网络方法探测数学模型误差[J].大坝观测与土工测试,2001,25(4):13-16.
[6] 刘红新,岳东杰.单参数快速搜索BP算法在GPS高程拟合中的应用[J].工程勘察,2003(1):54-56.
[7] 朱陶业,朱建军,张学庄,等.大气折射的映射函数与神经网络拟合比较分析[J].测绘学报,2007,36(3):290-295.
[8] 张昊,王琪洁,朱建军,等.样本数据预处理对基于BP神经网络的GPS高程拟合的影响[J].大地测量与地球动力学,2011,31(2):125-128.
[9] 鲁铁定,周世健,减德彦.关于BP神经网络转换GPS高程的若干问题[J].测绘通报,2003(8):7-9,15.
