基于相位校正的时差估计算法研究

柏如龙，闫 涛

（中国电子科技集团公司第五十四研究所，河北 石家庄 050081）

0 引言

长基线三站时差无源定位系统具有定位精度高、定位速度快、能同时处理多目标信号等诸多突出优点，在电子对抗领域获得了广泛应用。该系统通常采用地面固定三站配置模式，可以准确快速地获取监视空域内的态势信息。时差测量技术是该系统中的关键技术之一。对于短持续的脉冲信号，通常直接测量各站脉冲到达时间，然后通过站间脉冲配对再计算到达时差[1，2]。对于长持续的连续波信号，通常直接计算两站之间的互相关函数测量到达时差[3，4]。相关文献中在构建接收到的信号模型时，通常假定不同接收站之间的信号存在一个固定的起始相位偏差，而未考虑目标运动引起的多普勒频率的影响。在有些场合下，多普勒频率严重影响相关峰值的检测以及时差测量精度。本文针对多普勒频差对相关峰值检测和时差测量的影响进行了详细分析，提出了一种抵消多普勒频差影响的相位校正算法，实现了对运动目标的高精度时差估计。

1 多普勒频差影响分析

以主站信号为参考，接收到的主辅站信号x1（t）、x2（t）分别表示为[5]:

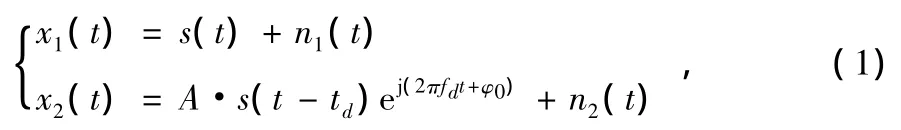
式中，s（t）为主站接收到的有用信号项，A为主辅站相对信号幅度，td为到达时差，fd为多普勒频差φ0为初始相位偏差，n1（t）和n2（t）为零均值加性高斯白噪声，且与信号互相独立。

x1（t）与x2（t）之间的二阶互相关函数表示为:

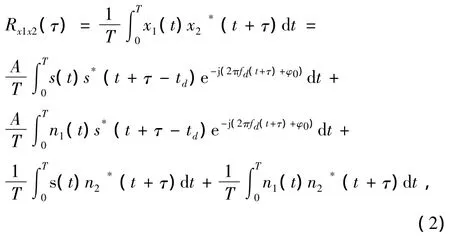
式中，T为积分时间。

在fd=0时，根据三角不等式和施瓦兹不等式，可以得到td的估计值:

式（3）表明，主辅站信号的相关输出在信号间的相对时延为td处取得最大。二阶互相关函数的输出信噪比SNRO以及时差测量精度στ的Cramer－Rao界表示为:

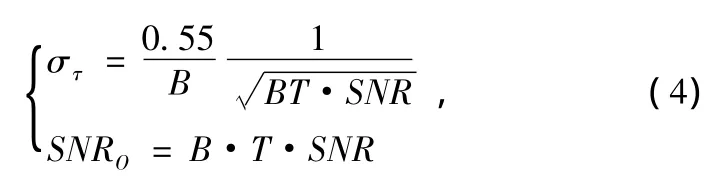
式中，B为信号带宽，SNR定义为:

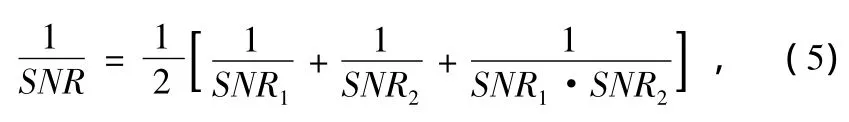
式中，SNR1、SNR2为主辅站信噪比。

在fd≠0时，式（2）中存在一个多普勒频差调制项e－j2πfdt，此时二阶互相关函数表示为:

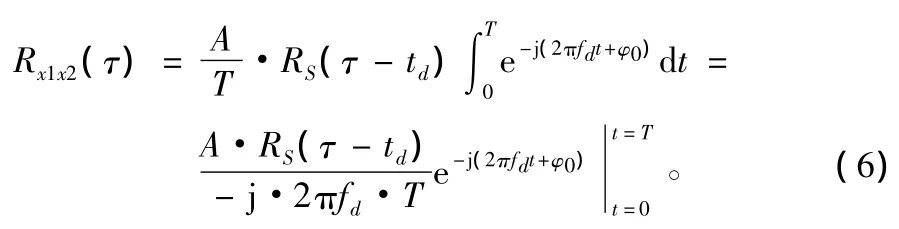
由式（6）得出，在积分时间内多普勒频差调制项引起的相关值衰减为:

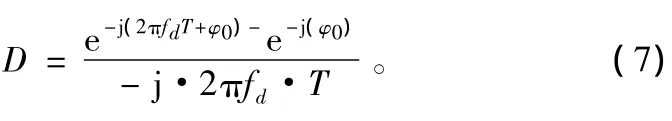
根据式（7）计算出不同积分时间下的相关值，得到相关值衰减曲线如图1所示，图中多普勒周期定义为多普勒频差的倒数。

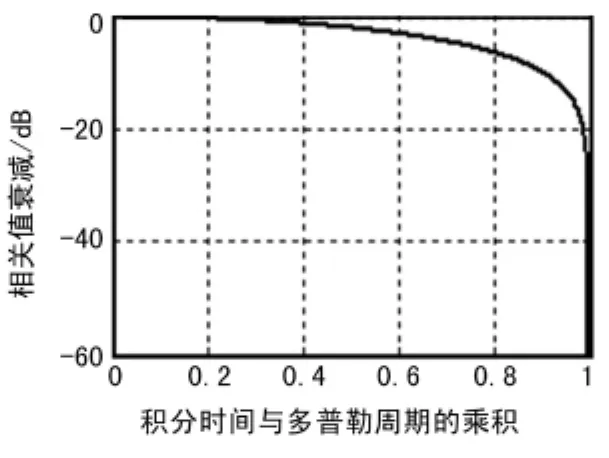
图1 相关值衰减曲线

分别讨论积分时间远小于多普勒周期和积分时间与多普勒周期近似相等两种典型情况下的相关值衰减值。当，此时相关值衰减约等于0dB，这表明对于积分时间远小于多普勒周期的情况，多普勒频差对二阶互相关函数几乎无影响。举例来说，某信号频率为1GHz，信号持续时间T=30μs，假定主辅站间的多普勒频差fd=10Hz，此时T·fd=0.003＜＜1，因此，多普勒频差对该信号的时差测量影响可以忽略。

当T=1/fd时，多普勒频差调制项使得在fd的一个周期内，相关峰完全被抑制，此时多普勒频差的影响不能忽视。举例来说，某信号的载频为300MHz，主辅站间的多普勒频差fd=3.33Hz，假如取积分时间T=0.3s，此时T·fd≈1，相关值近似为0，此时无法检测到有效相关峰值。

2 相位校正算法

多普勒频差随时间的累积引起主辅站信号间的相位差周期性变化，从而引起积分过程中的相关值衰减。如果能对主辅站信号间的相位差进行准确地估计，并对变化的相位差进行校正，使得在整个积分时间内的主辅站相位差为一个固定值，则此时互相关函数的输出无衰减。这就是相位校正算法的基本原理。

2.1 相位估计

通过较短数据的互相关，获得时差估计的粗值将主辅站信号调整基本对齐后，再精确估计主辅站信号间的相位差，相位差计算公式表示为:

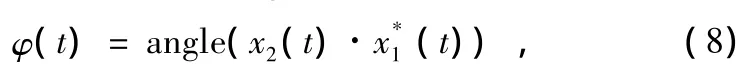
式中，angle表示取相位运算。对于计算过程中有可能出现相位模糊的情况，根据相位的跳变值解相位模糊。在采样率较高而多普勒频差较小的情况下采用分段积分降采样可以提高相位差的测量精度。

2.2 相位校正

以x1（t）为基准，对x2（t）进行相位校正x＇2（t）=x2（t）·e－j·φ（t），使得在整个积分时间内x＇2（t）与x1（t）相位差为0，此时互相关函数表示为:

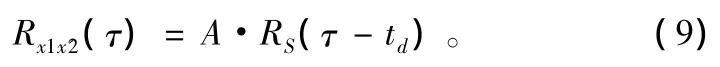
根据式（3）可知，式（9）在τ=td时取得最大值，且相关值无衰减。根据该峰值位置即可获得时差的估计值。

3 仿真分析

仿真条件设置:信号带宽为100kHz，调制样式为QPSK，采样率为500ksps，主辅站间的多普勒频差为5Hz，积分时间为0.1s，积分时间等于多普勒周期的一半，主辅站信噪比均为10dB。利用式（8）估计主辅站间的相位差，结果如图2所示。

设置主辅站的信噪比在5～20dB之间变化，根据式（4）计算得到时差测量精度的理论曲线。分别仿真不同信噪比条件下，相位校正前后时差估计误差曲线，如图3所示。

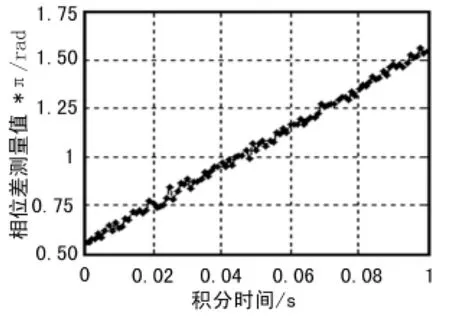
图2 积分时间与相位差测量值关系曲线

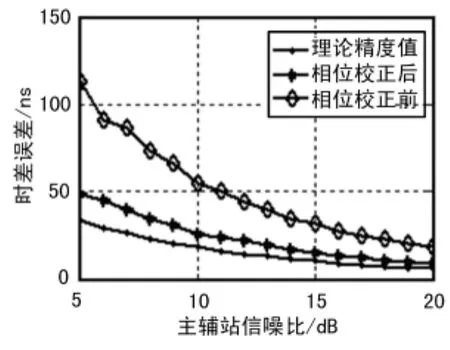
图3 相位校正前后时差估计误差曲线

在积分时间等于多普勒周期一半的情况下，从图3可以看出，如果未采用相位校正直接估计时差，其误差值约为理论值的2～3.5倍。采用相位校正后时差估计误差降为理论值的1.4倍，该值已经接近于无多普勒频差时所能达到的时差估计精度。

对比相位校正前后可以看出，时差估计精度提高了1.4～2.5倍，且已接近无频差时的估计性能这表明相位校正算法消除了主辅站间的相位偏差对相关积分的影响，从而提高了相关输出信噪比和时差测量精度。

4 结束语

多普勒频差对时差测量的影响不容忽视，特别是在处理长时间积分问题时，多普勒频差调制项严重影响了相关峰值的检测[6]。通过相位估计与相位校正处理，可以有效抑制多普勒频差对相关积分的影响该算法在改善相关输出信噪比和提高时差估计精度方面具有优越的性能，在快速运动目标的相关检测以及时差测量等领域具有广阔的应用前景。

[1]徐振鲁.时差法多站无源定位及其信号处理技术研究[D].南京:南京航空航天大学，2011.

[2]李剑峰.无源时差（TDOA）定位技术及其应用研究[D].成都:成都理工大学，2004.

[3]王俊凌，夏雄.时差测量方法对比分析[J].电子信息对抗技术，2008，23（6）:24－26.

[4]屈晓光，黄培康，朱可炎.对运动干扰源的时差估计[J].系统工程与电子技术，2000，22（5）:1－3.

[5]郭杨.基于时差测量的无线定位技术研究[D].长春:吉林大学，2005.

[6]耿志辉，柏如龙，基于倒谱域相关的时差/频差联合估计算法[J].无线电工程，2007，37（11）:26－27.