真空联合堆载预压大变形固结有限元分析
2013-05-13刘昌鸿马石城
刘昌鸿, 马石城
真空联合堆载预压大变形固结有限元分析
刘昌鸿*, 马石城
(湘潭大学 土木工程与力学学院, 湖南 湘潭, 411105)
利用有限元分析软件ABAQUS, 分别采用小应变理论和大变形理论, 对真空联合堆载预压法处理软基进行了仿真和固结分析. 根据固结度等效原则, 将砂井地基转换成平面应变砂墙地基, 将模拟数据与某公路监测段监测数据进行对比, 结果表明, 用大变形理论处理深厚粘土软基更为合理.
软基; 大变形; 真空联合堆载预压; ABAQUS
随着我国经济和交通基础建设的迅猛发展, 沿海地区的高速公路建设也进入了一个全新的时期. 与此同时, 我国沿海地区存在大量沉积软土, 由于软土的特殊性, 势必对高速公路的工后稳定和沉降产生影响. 因此, 有必要对软弱地基进行处理. 软基处理方法大体上可分为排水固结法、动力固结法、置换法、复合地基法. 这些处理方法都有各自的优点、适用范围和存在的问题. 从工期和造价两方面考虑, 通常选择真空联合堆载预压处理软弱地基. 但是工程界对真空联合堆载预压机理并没有形成统一的认识, 且以往的研究多集中于小变形, 并没有过多考虑到软粘土的高压缩性对沉降的影响. 在岩土工程中, 若土层压缩性较高, 沉降通常较大, 这时需要考虑大变形的影响. 因此, 本文依托杭金衢高速公路监测段工程实例[1—2], 借助ABAQUS对该工程进行大变形固结有限元分析, 并与监测数据进行对比分析.
1 大变形理论及基本方程
大变形固结理论[3]的一些基本假设实际上与Terzaghi理论是相同的, 不同的地方是压缩系数不再是一个常量, 渗透系数的取值跟孔隙比有关. 在有限元分析中, 对于处理大变形问题, Lagrangian法在引入本构关系和处理表面外荷载问题上有着独特的优势. 因此, 包括ABAQUS在内的许多岩土工程分析软件都采用该方法, 以下为Lagrangian描述的基本方程[4—5].
a. 几何方程. 大变形的形变条件要比小变形的形变条件复杂, Lagrangian描述的形变条件, 即格林应变张量表达式如下:

b. 平衡方程. 在外荷载的作用下, 变形体在变形之后重新达到平衡状态, 应力与应变存在相互联系, 因此平衡方程应当用变形以后的状态即现时构形的欧拉应力来描述, 方程描述如下:

c. 本构方程. 建立在物质构形基础上的本构方程为:
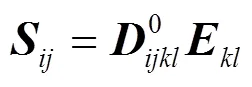
对应的增量形式为:

2 工程实例及有限元分析
2.1 工程及地质概况
杭金衢高速公路, 全长290 km. 该公路起点为杭州萧山红垦农场, 沿线经过萧山区、绍兴县、诸暨市、浦江县、义乌市、金华市金东区、金华市婺城区、兰溪市、龙游县、衢江区、衢州市等12个县(市、区), 终点为常山县窑上, 是浙江省穿越县市最多的高速公路. 该路线经过地区的地形、地貌具有东部沿海软弱地基特点, 土层物理力学指标较差. 本文选取K32 + 281—K32 + 417.5真空联合堆载预压段, 其工程地质条件为: 第1层为填土层, 厚约0.6 m, 在进行地基处理时已被挖除; 第2层为粘土层, 物理力学性质较差, 厚约2.0 m; 第3层为淤泥质粘土, 物理力学性质差, 约厚10.4 m; 第4层为淤泥质亚粘土层, 物理力学性质差, 约厚8.6 m; 第5层为亚粘土层, 约厚1.6 m; 第6层为砾砂层, 未钻穿.
2.2 模型的建立
2.2.1 几何模型
采用塑料排水板技术处理软弱地基的真空联合堆载预压是典型的三维问题, 从严格意义上来讲, 应当采用三维有限元模型来分析计算. 但由于三维有限元模型的计算成本过高, 实际中通常采用平面应变模型来分析砂井地基固结. 根据对称性原则, 以路堤的中心为基准线, 取地基的一半建立有限元模型. 根据该公路段相关设计资料及真空联合堆载预压的影响范围, 取地基的计算宽度80 m, 其中加固区为21 m, 影响区为59 m. 计算深度取22.6 m. 塑料排水板(厚4 mm, 宽100 mm)打设深度为22 m, 间距1.2 m, 平面呈三角形分布. 土体的计算参数采用修正剑桥模型[1], 其参数见表1.

表1 有限元计算参数
2.2.2 排水板单元
塑料排水板的截面尺寸与周围土体尺寸相比非常小, 其主要作用是作为竖向排水体增加渗透性. 在数值模拟中, 不考虑打设塑料排水板对本层土体带来的刚度变化. 对于有竖向排水设置的软基, 其固结和渗透往往以水平方为主, 因此通常只调整水平向渗透系数. 考虑到排水板的井径较小, 一般计算时可忽略其井阻和涂抹作用对塑料排水板的影响, 渗透系数等效公式为[6]:

式中,hp为平面应变条件下, 砂墙影响区域土层水平方向的渗透系数;h为轴对称条件下, 砂井影响区土层水平方向的渗透系数;为砂井(或塑料排水板)的井径比,=/w, 其中为砂井的有效排水半径,w为砂井半径;为砂墙间距的一半.
该模型中首先将塑料排水板等效为圆形砂井, 然后将砂井间距放大4倍, 取2= 4.8 m, 三角形布置,取0.63 m,取12, 从而得到hp/h= 5.6. 塑料排水板的渗透系数取h=v= 2´10-3cm×s-1.

图1 有限元网格划分
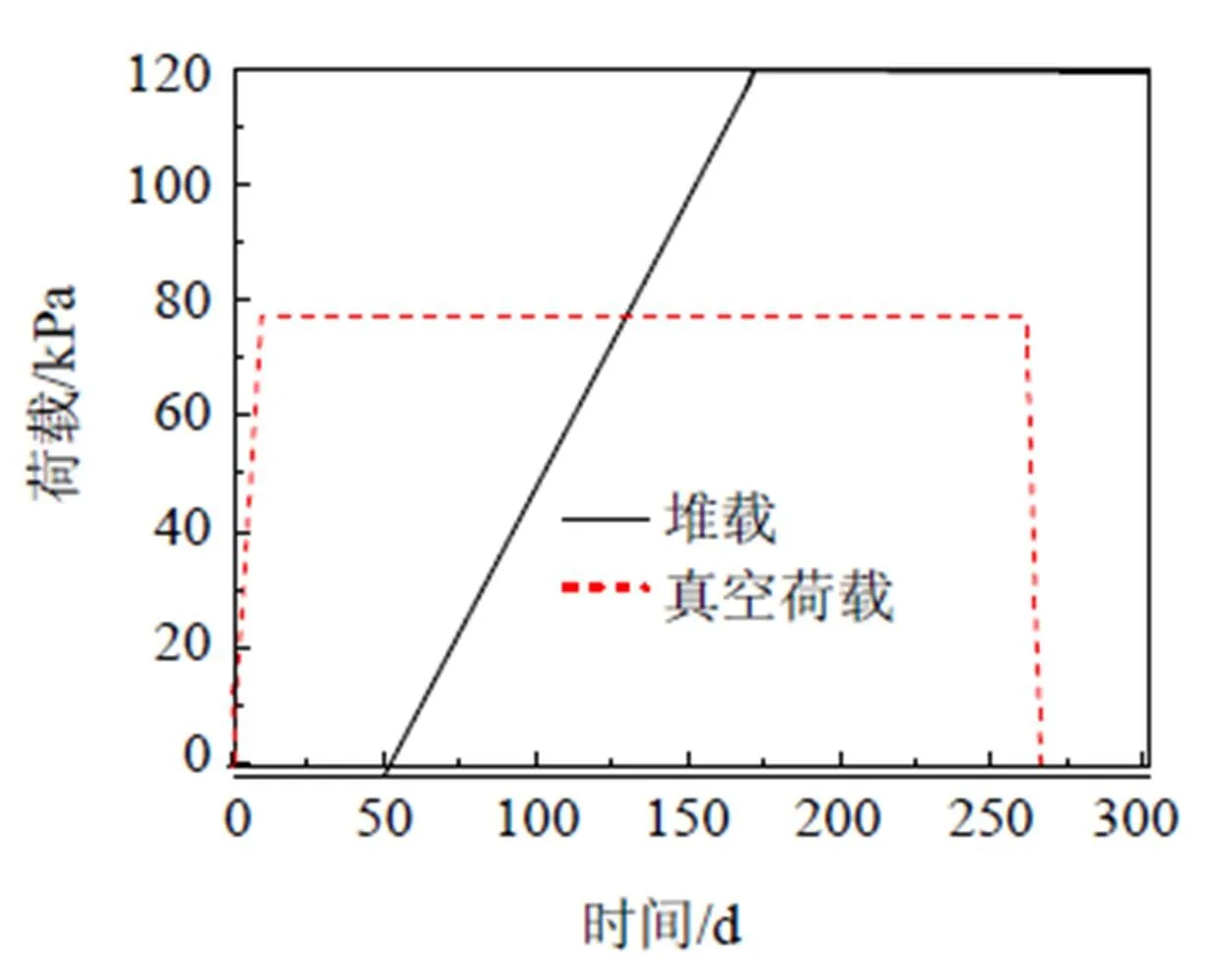
图2 真空预压曲线和堆载曲线
2.2.3 计算条件
在计算变形固结中, 大变形计算网格采用平面应变孔压线性单元(CPE4R), 小变形采用二阶缩减积分单元(CPE8R)[7], 结构化网格划分. 网格靠近加固区域划分较密, 往远处逐渐变稀疏. 具体网格划分情况如图1所示.
位移边界条件为: 左右两边约束为方向的位移, 底边约束为方向位移, 顶面为自由边界.
渗透边界条件为: 左右两侧和底边均为不透水边界, 上部边界为透水边界.
在计算真空预压时, 让加固区表面各点的孔压在一定时间内按线性变化从0减少到-80 kPa, 然后稳定在-80 kPa; 堆载时, 按实际的加载曲线加载. 真空卸载时, 也让孔压在一定时间内线性减少. 真空荷载和堆载荷载的加载曲线如图2所示. 由于模型在计算时应考虑地下水位变化的影响, 因此将地下水位变化引起的相当荷载预先施加到地基表面上.
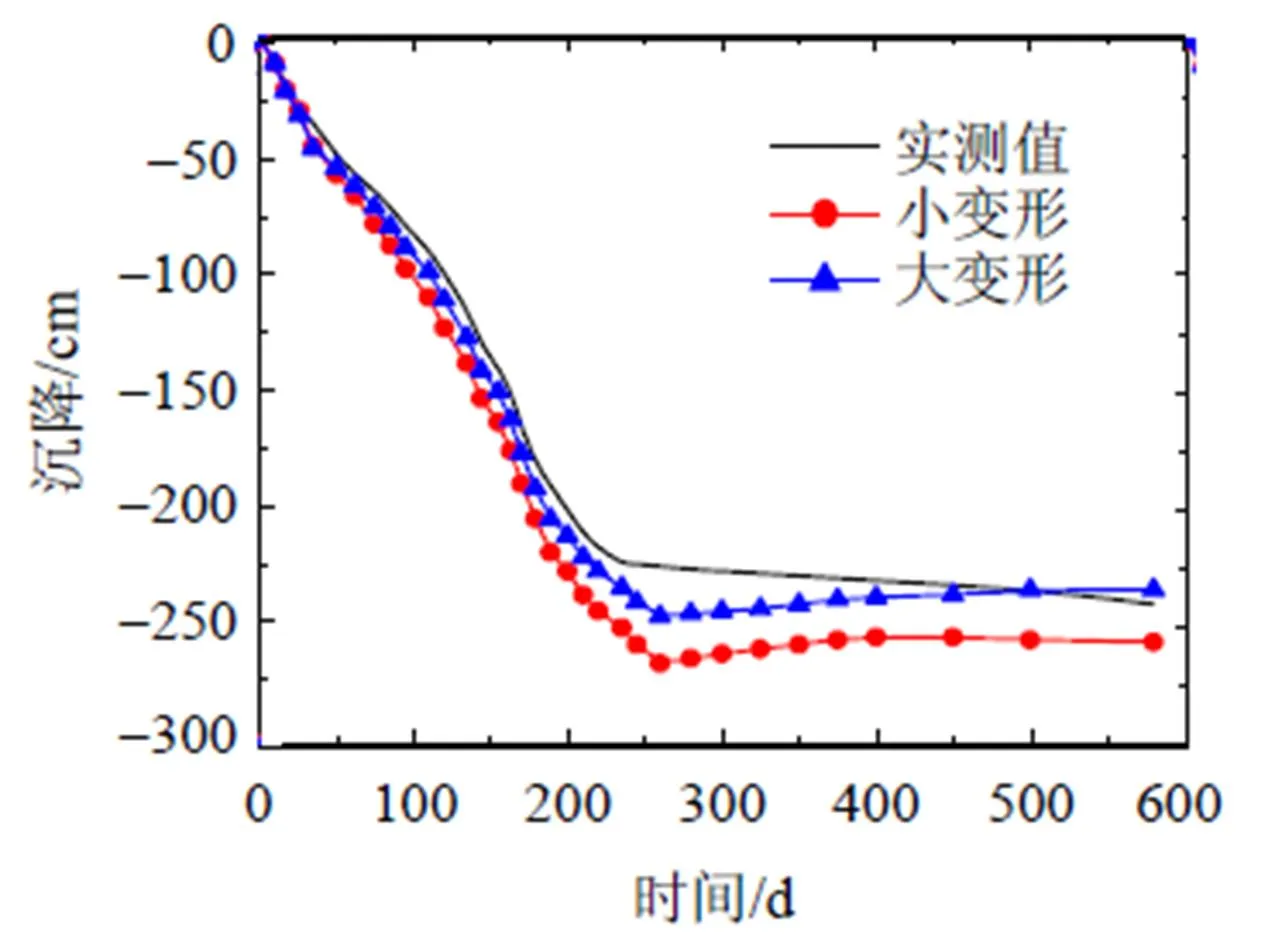
图3 加固区中心表面沉降
2.3 计算结果分析
2.3.1 大小变形固结条件下地基表面中心点沉降对比
图3为加固区中心点固结沉降随时间的变化曲线. 图3中3条曲线分别为大变形, 小变形的计算结果和现场实测值曲线. 从图3可以看出, 无论是大变形还是小变形, 沉降曲线都与实测曲线基本相似, 其中利用大变形计算出来的结果更加接近实际. 其次, 有限元计算中同样出现了这样一个现象: 即卸除真空荷载时, 大小变形都出现了一个较明显的回弹, 这与文献[1]中提到的情况基本一致. 此外, 由于土体参数获取的局限性, 从而造成模型的计算结果与实际情况仍然存在着一定的差距, 但总体来说, 固结有限元的计算结果还是比较令人满意的.

图4 5 m深处加固区中心分层沉降
2.3.2 大小变形固结在不同深处的分层沉降对比
图4、图5、图6分别为大小变形固结在不同深处条件下计算出来的分层沉降量. 从图中可以看出, 大变形计算出来的沉降量小于小变形计算出来的沉降量, 但大小变形所计算出来的分层沉降量之间的差距随着深度的加深而逐渐减小, 在22 m深处大小变形计算出来的沉降量基本趋于一致.

图5 10 m深处加固区中心分层沉降

图6 22 m深处加固区中心分层沉降
3 结语
a. 采用真空联合堆载预压法加固软弱地基效果明显, 能够加快地基固结速率, 有利于对工后沉降的控制.
b. 从分层沉降的数值计算情况来看, 大小变形之间的差距主要集中在沉降量大的土层中, 而沉降量较小的土层大小变形计算出来的结果基本趋于一致.
c. 大变形固结理论计算出的竖向最终沉降量要小于小变形理论计算出来的最终沉降量. 两者的沉降曲线走势规律与实测值基本一致, 考虑几何非线性效应的大变形沉降曲线和水平位移曲线更加接近实测值, 说明用大变形固结理论处理高压缩性的软弱地基是合理的.
[1] 刘汉龙, 彭劼, 陈永辉, 等. 真空-堆载预压处理高速公路软基的有限元计算[J]. 岩土力学, 2003, 24(6): 1029—1033.
[2] 彭劼. 真空-堆载联合预压法加固机理与计算理论研究[D]. 南京: 河海大学, 2003.
[3] 钱家欢, 殷宗泽. 土工原理与计算[M]. 北京: 中国水利水电出版社, 1995: 229—233.
[4] 房峻松, 高明军. 负压下软土大变形数值分析[J]. 西部探矿工程, 2006(2): 56—58.
[5] 何开胜, 沈珠江, 彭新宣. 两种Lagrangian大变形比奥固结有限元法及其与小变形法的比较[J]. 岩土工程学报, 2000, 22(1): 30—34.
[6] 廖公云, 黄晓明. ABAQUS有限元软件在道路工程中的应用[M]. 南京: 东大学南出版社, 2008: 229—230.
[7] 邝立文. 饱和软土的Boit大变形固结有限元分析[D]. 广州: 暨南大学, 2010.
The finite element analysis of large deformation consolidation on vacuum-surcharge preloading
LIU Chang-hong MA Shi-cheng
(College of Civil Engineering and Mechanics, Xiangtan University, Xiangtan 411105, China)
By the ABAQUS software, the process of vacuum-surcharge preloading on soft foundation is simulated, and its consolidation of settlement is analyzed. The simulation during vacuum-surcharge preloading with small deformation theory and large deformation theory are separately computed. According to the principle of equivalence of the consolidation degree, sand-drained ground will be converted into plane strain sand wall foundation. Combined with a highway monitoring segment, the simulation data are compared with monitoring data. Data analysis shows that the large deformation theory on treating deep soft clay was more reasonable.
soft foundation; large deformation; vacuum-surcharge preloading; ABAQUS
10.3969/j.issn.1672-6146.2013.01.015
TU 348
1672-6146(2013)01-0059-04
email: 383503540@qq.com.
2013-03-05
(责任编校: 江 河)
