锡硫化合物第一性原理研究

彭跃华



锡硫化合物第一性原理研究

彭跃华*

(湖南师范大学 物理与信息科学学院, 湖南 长沙, 410081)

为了解锡硫化合物的性质, 对Sn-S体系中化合物进行了第一性原理研究, 优化了Sn-S体系中化合物的结构. 研究表明计算时采用局域密度近似(LDA)比广义梯度近似(GGA)能更好地描述该体系的交换-相关能, 从而在对该体系进行进一步研究时, 采用LDA进行计算能得到更好的优化结果. 计算所获得该体系化合物形成能及结合能的计算结果显示, 在形成化合物过程中SnS2优先于Sn2S3形成.

锡硫体系; 密度泛函理论; 第一性原理; 交换-相关能

有关Sn-S二元体系的研究主要集中于20世纪60年代, 研究者[1—3]反复实验测定了其相图, 并对体系的二元化合物进行了广泛的研究[4—7]. 直到1986年, Sharma[8]总结了之前的数据, 得出Sn-S合金的二元相图. Sn-S二元体系存在三个化合物SnS、Sn2S3和SnS2, 该3个化合物均存在b晶型与a晶型之间的转变, 相对应的转变温度分别为602 ℃、680 ℃和691 ℃. 本文的相关实验温度均在600 ℃以下, 仅对SnS、Sn2S3和SnS2三种化合物的a晶型结构进行研究. 但是S在液相Sn中的溶解度很小, 甚至在600 ℃时也不超过2.0 at.％, 同样温度下, Sn在液相S中的溶解度也未达到2.0 at.％.

近年来随着相关理论和数值算法的飞速发展, 使得基于密度泛函理论的第一性原理[14]方法成为凝聚态物理、量子化学和材料科学中的常规计算研究手段, 其计算精度也被众多的学者所证实. CASTEP软件使用量子力学程序, 是基于密度泛函理论下使用赝势和平面波基组, 进行从头量子力学分子动力学计算的软件包[15—17]. 将量子力学和分子动力学相结合, 采用固体物理中的Bloch定理处理周期性固态晶格波函数问题, 用单位晶格电子的计算来简化对无限多个单电子的周期性晶格的研究. 波函数简化利用无限平面波基底展开, 由于高阶动能项贡献较小, 可将其省略, 仅保留低阶动能项, 而原子真实的库仑势能采用赝势来取代, 同时忽略内层电子效应, 只处理价电子的部份. 对于多电子间的交换相干能, 利用局域密度近似和广义梯度近似方式处理, 可以相对减少计算量, 通过对微观尺度的模拟, 来预测材料特性. 本文采用CASTEP第一性原理计算软件包对Sn-S体系化合物进行结构优化, 对其形成能和结合能进行计算.

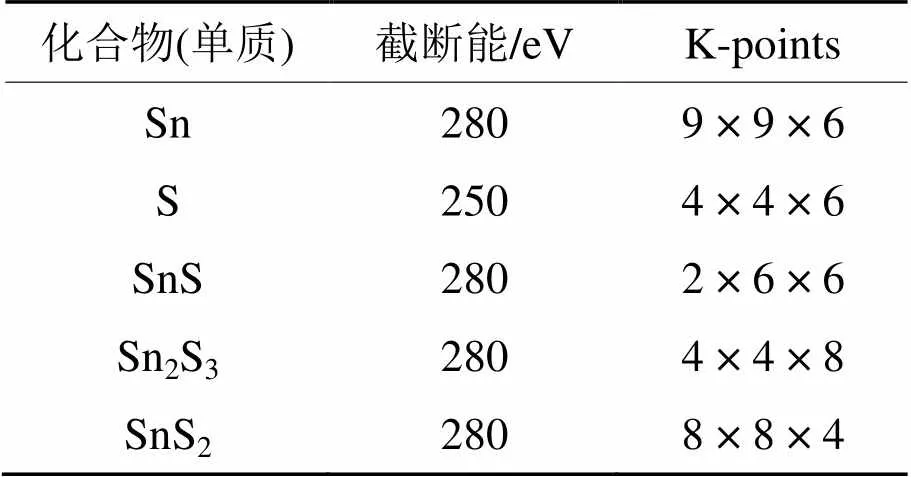
表1 计算中单质和化合物使用的截断能及K-points参数

1 计算方法

计算中基于密度泛函理论(DFT)及赝势平面波法, 在计算晶格常数、合金形成能和结合能时, 利用周期性边界条件, 分别对Sn、S、SnS、Sn2S3、SnS2进行计算. 晶格常数和能量的计算分别采用局域密度近似(LDA)和广义梯度近似(GGA)进行对比, 晶体波函数用平面波基来展开, 交换关联能函数采用GGA近似的Perdew-Burke-Ernzerh(PBE)形式, 赝势的选择为平面波超软赝势(Ultra-soft Vanderbilt)方法. 计算中除S和Sn2S3以外, 均使用了软件默认最精确的参数. 其截断能及K-points参数见表1. 布里渊区(BZ)的取样根据Monkhorst–Pack方法, 对结构的优化采用了Broyden Flecher Goldfarb Shanno (BFGS)方法, 自洽计算时采用Pulay密度混合法, 体系总能量的收敛值取5.0 × 10-6eV/atom (1 eV/atom = 96.48 kJ/mol[18]), 每个原子所受的力低于0.1 eV/nm, 公差偏移量小于5.0 × 10-3nm, 应力偏差量小于20 MPa.

形成能[18](Formation Energy)是指原子由单质状态形成为化合物时所释放的能量, 因此用化合物的总能减去其单质组元的能量即可得到形成能, 形成能能反映出材料的稳定性. 相对应的结合能(Cohesive Energy)[18]是指弧立原子结合成稳定晶体的过程中所释放出来的能量, 同样可以理解为把晶体分离成相距无限远的孤立离子所需的能量, 结合能反映了原子之间结合的强弱. 结合能将影响到合金的膨胀系数、弹性模量等宏观性能. 本文分别采用式(1)和式(2)计算Sn-S体系中各化合物的形成能form和结合能coh.

合金的形成能可由下式求得:

化合物的结合能可以由下式求得:

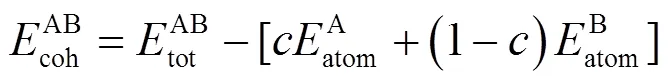
2 结果与讨论

2.1 结构优化

利用文献[9—13]中的相关晶体结构数据, 在CASTEP下构建晶体结构, 分别用广义梯度近似(GGA)和局域密度近似(LDA)描述交换-相关能对这些结构进行优化, 得到的结果见表2.

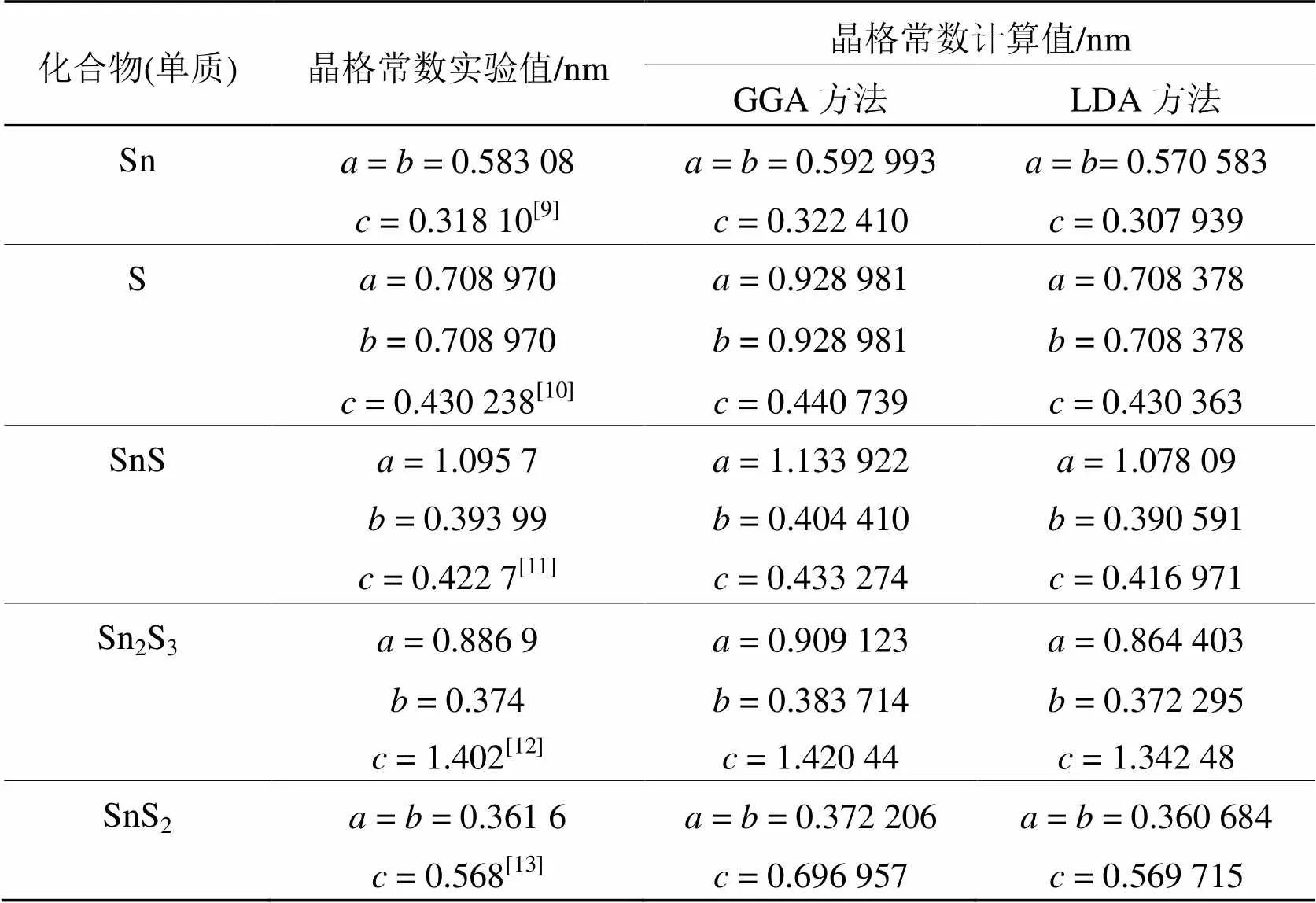
表2 Sn-S体系中单质和化合物晶格常数实验值与计算值对比

从表2可以看出, 采用LDA和GGA描述交换-相关能时, 优化后得到的晶格常数之间存在较大差距. 整体来说, 使用GGA优化后得到的晶格常数值与实验值相比偏大, 尤其对S而言, 晶格常数和的GGA优化值偏差达到30%以上, 超出了可信范围. LDA的偏差相对来说较小, 当前的第一性原理计算结果表明, LDA比GGA能更好地描述该体系的交换-相关能, LDA很大程度上改进了原子的交换-相关能计算结果, 从而得到相对较准确的计算结果. 整体而言对Sn-S体系化合物在进一步使用第一性原理对该体系进行研究时, 选用LDA描述交换-相关能对其进行优化计算有利于得到更优的计算结果. 同时, 由表2中的晶格常数对比还可以发现, 第一性原理优化得到的简单六方结构SnS晶格常数与实验值十分接近, 尤其是LDA函数优化结果. 对Sn2S3而言, LDA计算出值与实验值相比偏大.

2.2 Sn-S体系中化合物形成能与结合能

在计算孤立状态下的原子能量时, 建立一个1 nm × 1 nm × 1 nm的P1结构的格子, 在其中心位置的相对坐标为(0.5, 0.5, 0.5)处, 放置一个Sn原子或S原子, 再对它进行原子位置和结构方面的优化, 当优化完时体系的能量就是相应状态原子的能量. 计算Sn-S体系中化合物得到的形成能和结合见表3.用GGA和LDA计算得到的结果存在一定的差异, 这与优化时晶格常数的差异是密切相关的, 根据之前晶格常数的优化结果与实验值的比较, 采用LDA函数优化得到的结果更可靠.

表3 Sn-S体系中化合物平衡体积下系统总能量、形成能及结合能

由表3中数据可知: SnS、Sn2S3、SnS2的形成能均为负值, 且其负值均较大, 说明这些化合物都是稳定存在的. 同时表中数据显示Sn2S3的形成能最高, SnS2的形成能最低, SnS形成能值处于二者之间, 意味着在Sn-S体系中SnS2将会优于Sn2S3形成. 在相关的试验过程中也发现SnS2的形成相对较为容易形成, 而Sn2S3纳米线形成过程中需在Pb作为催化剂的条件下才能优势生长, 金属铅原子的出现能显著降低Sn2S3一维纳米结构的生长温度.

3 结论

本文采用CASTEP计算软件包对Sn-S体系中化合物进行了第一性原理研究, 优化了Sn-S体系中化合物的结构, 并对它们的形成能、结合能进行了计算. 研究表明计算时采用LDA比GGA能更好地描述该体系的交换-相关能. 采用LDA优化计算后得到的结果与实验值差异不大, 从而在对该体系进行进一步研究时, 采用LDA进行计算能得到更好的优化结果. 对该体系化合物形成能及结合能的计算结果表明, 在形成化合物过程中SnS2将会优于Sn2S3形成, Sn2S3纳米线形成过程中需在Pb作为催化剂的条件下才能优势生长, 该结论与实验结果相符.

[1] Albers W, Schol K. The P-T-X phase diagram of the system Sn-S[J]. Philips research reports, 1961, 16: 329—342.

[2] Karahanova M I, Pashinkin A S, Novoselova A V. On the melting diagram of Sn-S[J]. Akad Nauk SSSR Neorg Mat, 1966, 2(6): 991—995.

[3] Albers W, Haas C, Vink H, et al. Investigations on SnS[J]. Journal Of Applied Physics, 1961, 32(10): 2220—2225.

[4] Chattopadhyay T, Pannetier J, VonSchnering H G. Neutron diffraction study of the structural phase transition in SnS and SnSe[J]. Journal Of Physics And Chemistry Of Solids, 1986, 47(9): 879—885.

[5] Schnering H G, Wiedemeier H. The high temperature structure of β-SnS and β-SnSe and the B16-to-B33 type lambda transition path[J]. Zeitschrift für Kristallographie, 1981. 156(1/2): 143—150.

[6] Bok L D C, Boeyens I C A. Preparation of double metal-sulphides of the type AB2S4 Part. 2 Compounds of tin[J]. J South Africa Chem Inst, 1957. 10(2): 49—52.

[7] Mootz D, Puhl H. Die Kristallstruktur von Sn2S3[J]. Acta Crystallographica, 1967. 23(3): 471—476.

[8] Sharma R, Chang Y. The S-Sn (Sulfur-Tin) system[J]. Journal Of Phase Equilibria, 1986. 7(3): 269—273.

[9] Wocyrz M, Kubiak R, Maciejewski S. X-ray investigation of thermal expansion and atomic thermal vibrations of tin, indium, and their alloys[J]. physica status solidi (b), 1981. 107(1): 245—253.

[10] Crichton W, Vaughan G, Mezouar M. In situ structure solution of helical sulphur at 3GPa and 400 °C[J]. Zeitschrift für Kristallographie 2001. 216(8): 417—419.

[11] Slipukhina I, Bercha D. Elementary energy bands in isovalent IV-CVI orthorhombic and cubic crystals and their solid solutions[J]. physica status solidi (b), 2007. 244(2): 650—668.

[12] Cruz M, Morales J, Espinos J, et al. XRD, XPS and 119 Sn NMR study of tin sulfides obtained by using chemical vapor transport methods[J]. Journal Of Solid State Chemistry, 2003. 175(2): 359—365.

[13] Hazen R M, Finger L W. The crystal structures and compressibilities of layer minerals at high pressure; II, phlogopite and chlorite[J]. American Mineralogist, 1978. 63(3/4): 293—296.

[14] 朱建新, 李永华, 孟繁玲, 等. Ni-Ti合金的第一原理研[J]. 物理学报, 2006. 55(11): 6032—6035.

[15] 张跃, 谷景华, 尚家香, 等. 计算材料学基础[M].北京: 北京航空航天大学出版社, 2007: 83—118.

[16] Clark S J, Segall M D, Pickard C J, et al. First principles methods using CASTEP[J]. Zeitschrift Für Kristallographie, 2005. 220(5/6): 567—570.

[17] Lindan P J D. First-principles simulation: ideas, illustrations and the CASTEP code[J]. Journal of Physics: Condensed Matter 2002. 14(11): 2717—2744.

[18] Tang B Y, Yu W Y, Zeng X Q, et al. First-principles study of the electronic structure and mechanical properties of CaMg2 Laves phase[J]. Materials Science and Engineering A, 2008. 489(1/2): 444—450.

Study of first-principles of Sn-S compounds

PENG Yue-hua

(College of Physics and Information Science, Hunan Normal University, Changsha 410081, China)

In order to understand the properties of Sn-S compounds and optimize the structure of the Sn-S compounds, compounds of Sn-S system have been studied by the first-principles. The result shows that LDA was better to describe exchange-correlation energy of this system than GGA, which in the system for further study, using LDA calculated can get better optimization results. As shown in calculation results for the system compounds formation energy and binding energy, SnS2was preferential formation to Sn2S3in the process of compounds formation.

Sn-S system; density function theory; first-principles; exchange-correlation energy

10.3969/j.issn.1672-6146.2013.03.005

O 561

1672-6146(2013)03-0025-04

email: yhpeng@hunnu.edu.cn.

2013-07-22

湖南师范大学青年科学基金项目(11102), 湖南省教育厅资助科研项目(12C0191).

(责任编校: 江 河)