预测油田水驱油效率四参数模型
2013-05-13刘道杰田中敬龚晶晶
刘道杰,田中敬,龚晶晶
李海东,崔建
(中石油冀东油田分公司勘探开发研究院,河北 唐山063004)
预测油田水驱油效率是油藏工程领域中的一个重要研究内容,对制定油田开发方案,预测油田最终采收率,精细描述剩余油微观分布特征及研究油藏水淹状况具有重要意义。纵观国内外相关文献,预测油田水驱油效率主要采用经验公式、室内试验及数学方法[1~8]。一般相关经验公式及数学方法都是基于数理统计方法获得的,没有考虑油藏物性等内部信息变化特征,其预测精度难以得到保证;而室内水驱岩心试验是在模拟油藏条件下进行的,因而能够准确反映油藏内部信息变化特征,预测的水驱油效率一般比较准确。笔者以室内水驱岩心试验测试的数据信息为基础,建立了四参数模型预测油田水驱油效率的方法。
1 预测水驱油效率的四参数模型
假设油藏采用注水开发,极限驱油效率ηd,lim利用下式进行计算:

式中:ηd,lim为含水率达到1.0时的极限驱油效率,1;Soi,Sor分别为原始含油饱和度、残余油饱和度,1。
对于特定的油藏,Soi一般比较容易确定,而Sor由于受多方面条件限制,其测试值误差较大。因此ηd,lim很难准确计算,一般将其作为一个未知数。
新型增长曲线模型研究了累积产气量与生产时间的关系[9],实际研究表明[10~12],油藏水驱油效率与生产时间的变化关系也符合新型增长曲线模型。因此,笔者尝试以试验测试的数据资料为基础,利用新型增长曲线拟合油藏驱油效率与生产时间的关系:

式中:ηd为油藏驱油效率,1;t为油藏生成时间,a;aj(j=1,2,3)为模型参数。
由于模型中包含ηd,lim、a1、a2、a3共4个未知参数,式(2)可作为预测驱油效率的四参数模型。利用式(2)拟合驱油效率与时间的关系后,就可以利用拟合曲线预测油藏驱油效率。该模型适用于预测不同类型油藏水驱油效率。
四参数模型计算值与试验值的平均相对误差εr,avg由下式计算:

式中:ηd,exp、ηd,cal分别为驱油效率试验值和模型计算值,1;n为试验数据组数。
2 模型求解
对于预测驱油效率的四参数模型,只要求出模型中ηd,lim、a1、a2、a3这4个未知参数,就可以对式(2)进行回归,从而预测油藏不同时间对应的水驱油效率。
利用室内水驱岩心试验获得驱油效率与生产时间的数据序列,首先采用非线性回归方法对离散的数据序列进行回归,获得连续的方程;然后,利用多变量寻优算法求解,获得ηd,lim、a1、a2、a3这4个模型参数。
若试验测定n组数据,将式(2)转化为求解目标函数:
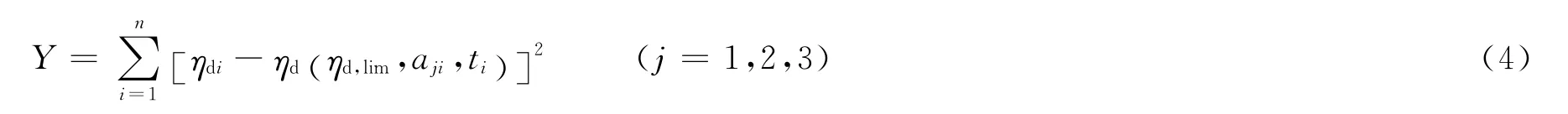
式(4)即为四元非线性方程。若要求解Y的极值,则需满足:

利用泰勒公式对式(4)展开,取至二阶项即可满足精度要求,得:

对式(7)求导:

由式(8)和式(9)求导得到线性化方程组,求解方程组即可获得ηd,lim、a1、a2、a3,从而获得预测油藏驱油效率的拟合方程。
3 实例计算与分析
以某水驱砂岩油田为例。油田地质储量为8240×104t,平均有效厚度为18.2m,孔隙度为36.1%,原始含油饱和度为59%,储层空气渗透率为1810mD。油田自1972年4月投产,两年后实施注水开发。通过室内水驱岩心试验获得驱油效率与生产时间的数据序列,利用四参数模型对试验测试的驱油效率与生产时间进行拟合,对模型求解得到模型的4个参数ηd,lim=0.6943、a1=1.47062、a2=0.92701、a3=-1.30721,相关系数R2=0.9978,其拟合方程式为:

将生产时间代入式(10)中,获得四参数模型计算的驱油效率值,将其与试验值进行对比(图1),拟合值与试验值的平均相对误差为0.57%。由图1可以看出,试验值基本都落在模型拟合曲线上,说明拟合曲线与试验值符合得非常好。
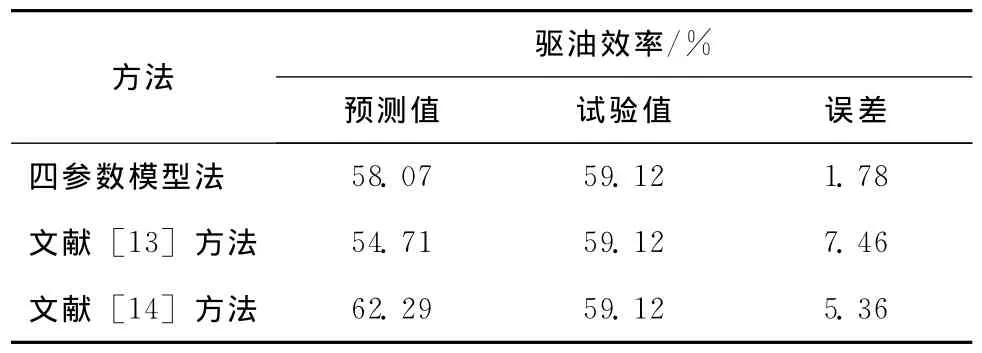
表1 不同方法预测油田水驱油效率对比
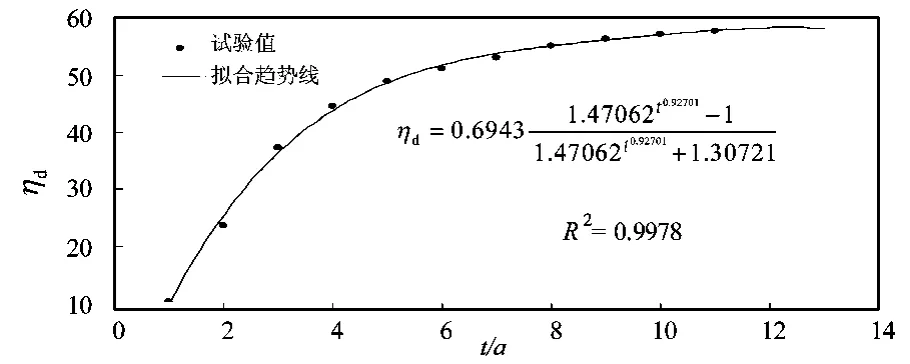
图1 四参数模型拟合曲线
水驱砂岩油田通过室内水驱岩心试验获得的油田水驱油效率为59.12% (表1);文献 [13]利用建立的驱油效率预测模型计算该油田的水驱油效率为54.71%,与试验值的平均相对误差为7.46%;文献[14]利用矿场生产资料预测该油田水驱油效率为62.29%,与试验值的平均相对误差为5.36%。由于四参数模型法考虑了油藏内部信息变化特征对驱油效率的影响,拟合方程式 (10)预测该油田水驱油效率为58.07%,与试验值59.12%非常接近,其平均相对误差为1.78%。由此说明,利用四参数模型预测油田水驱油效率是可行的,准确的。
4 结 论
1)对于一般性的油田,首先通过拟合驱油效率与生产时间的关系,获得四参数模型拟合方程;然后将未来生产时间输入到拟合方程中,即可预测得到不同时间对应的水驱油效率。
2)实例表明,获得的水驱油效率拟合曲线与试验值符合得比较好,说明四参数模型拟合水驱油效率是可行的。
3)利用四参数模型预测某油田的水驱油效率平均相对误差为1.78%,较其他方法预测的平均相对误差7.46%和5.36%更精确。由此论证了该方法的有效性、准确性和可靠性。
[1]Wu Wenxiang,Wang Demin,Jiang Haifeng.Effect of the visco-elasticity of displacing fluids on the relationship of capillary number and displacement efficiency in weak oil-wet cores [J].SPE109228,2007.
[2]Clerke E A.Permeability and microscopic displacement efficiency of M _1bimodal pore systems in Arab-D limestone [J].SPE105259,2007.
[3]刘红现,许长福,覃建华,等 .砾岩油藏孔隙结构与驱油效率 [J].石油天然气学报 (江汉石油学院学报),2010,32(4):189~191.
[4]秦国伟,蒲春生,罗明良,等 .不同粘弹性驱替液下毛管数对驱油效果的影响 [J].石油天然气学报 (江汉石油学院学报),2007,29 (2):97~100.
[5]Trivedi J J,Babadagli T.Efficiency of miscible displacement in fractured porous media [J].SPE100411,2006.
[6]Savery M,Darbe R,Chin W.Modeling fluid interfaces during cementing using a 3Dmud displacement simulator [J].SPE18513,2007.
[7]Afrapoli S,Nikooee E,Alipour S.Experimental and analytical study of microscopic displacement mechanisms of MIOR in porous media[J].SPE143722,2011.
[8]贾忠伟,杨清彦,兰玉波,等 .水驱油微观物理模拟实验研究 [J].大庆石油地质与开发,2002,21(1):46~49.
[9]俞启泰 .预测油气田开发指标的btc因子型增长曲线 [J].天然气工业,2001,21(2):79~81.
[10]何贤科,陈程 .用动态资料预测注水开发油田驱油效率 [J].新疆石油地质,2005,26(3):296~297.
[11]王者琴,吴晓慧,张永梅,等 .水驱曲线和相对渗透率曲线联用计算分类井地质储量 [J].大庆石油地质与开发,2007,26(6):61~63.
[12]王勇刚,文志刚,陈玲 .特低渗透油藏水驱油效率影响因素研究——以西峰油田白马中区长8油层为例 [J].石油天然气学报 (江汉石油学院学报),2009,31 (4):284~288.
[13]李奋 .中高渗砂岩油藏水驱油效率及波及规律研究 [D].东营:中国石油大学 (华东),2009.
[14]颜子 .利用矿场生产资料预测水驱驱油效率方法探讨 [J].油气地质与采收率,2010,17(3):99~101.
