最后要价仲裁机制下的纳什均衡与福利分析①
2013-05-12鲍传健
沈 越 鲍传健
一、引 言
一项经济活动中的参与人就各自的利益讨价还价不能达成一致时,除了诉诸法律外,一个有效率的仲裁制度可以起到很大的作用。目前,有两种仲裁机制被广泛应用。在传统意义上的仲裁制度(Conventional Arbitration,CA)下,给定参与者的要价,仲裁者依据自己的偏好确定一个最终的结果。直觉上这里存在的问题是,一般而言,仲裁者会综合考虑参与方的叫价,折中 (Split the difference)形成最后的解决方案。重要的是,参与人会预期到仲裁者的这种偏好,于是,各自便有激励出更极端的价格。考虑一个劳资纠纷的例子,工会希望高工资,资方偏好低工资,在传统仲裁机制下,如果参与双方预期到仲裁者折中双方叫价,则参与人出相对极端价格的激励是显而易见的。实际中也可以见到这样的例子。而且,有些部门是不允许以罢工等相对极端的形式来达到目的的,典型的如警察和消防员。当这类公共部门产生工资纠纷时,仲裁便可以起作用。正是在这样的背景下,经济学家们提出了一种被称为最后要价仲裁 (Final-Offer Arbitration,FOA)的新机制,意图减轻传统仲裁的这种激冷效应。(chilling effect)Stevens的开创性论文最先提出了这种机制,其核心是,仲裁者在决定最终方案时,不能进行任何的妥协或折中,而只能选择其中一方的出价作为最终解决方案。〔1〕这种机制的设计是希望通过赋与参与者更大的不确定性,促使纠纷双方更严肃地进行谈判或协商,从而达成一致,避免通过仲裁解决。这里的假定是,从福利的角度看,协商解决优于仲裁方案,毕竟后者会至少有一方不满意。正如Long和Feuille指出的那样:“……一个成功的最后要价程序是没有使用的那一个……”。〔2〕Nelson也认为,“FOA的目标是使仲裁成为不必要”。〔3〕
FOA程序在国外被广泛地应用,如美国棒球大联盟球员的工资决定就是经常被引用的例子。实际上可以说,FOA机制在国外的应用已经相对成熟,在劳动纠纷,商业合同纠纷,环境纠纷,民事法改革等场合,都可以看到FOA机制的影子。甚至选举也可以被视作一个FOA程序:两个选举人进行零和博弈,由选民投票决出胜者。设计FOA机制的目的是希望减轻激冷效应,其引致谈判或协商解决方案的能力被视为是否有效的重要指标。可实际效果如何呢?自从Stevens(1966)以后,很多文献从不同角度讨论了FOA的有效性。Crawford分析了FOA结果,对FOA引致协议的能力提出了质疑,并基于Donn(1977)的工作抽出了两种基于FOA的变形。〔4〕Farber在严格的假设下模型化了FOA,将之视为一个分馅饼的过程,两个参与人就各自的所得份额进行讨价还价,并讨论了风险态度对参与人合同区域的影响,认为更加重视风险规避的参与人出价将更加合理,从而,被选择的概率会更高。〔5〕而当不确定性增加时,最后出价将会倾向于发散。其方法被后来的很多文献采用。不过,他对于罗斯切尔德-斯蒂格利茨 (Rothschild-Stiglitz)意义上的风险度量的应用是错误的。〔6〕Brams和Merrill基于Farber的文章讨论了FOA机制下参与人的策略行为,给出了更加直观的表达。〔7〕〔8〕Wittman 首次引入了仲裁者偏见的影响,讨论了纳什均衡存在的条件,证明了参与一方的风险规避的程度增加,并导致双方参与人偏离各自的出价。〔9〕Samuelson将FOA机制模型化为不完全信息下的博弈行为,讨论了参与人风险态度的影响。〔10〕Hurley引入了多个仲裁者对FOA方案的影响,证明,满足一定假设下,参与人的出价确实存在一个收敛的均衡。〔11〕还有一些学者提出了刻画了FOA的变形,以期达到减轻激冷效应的目的。 (参见Brams 和 Merrill〔12〕、Zeng 等〔13〕、Zeng。〔14〕)但这些理论上有理的机制,目前还没有在实际中被采用。另外,实证研究的结果,从目前来看,也是不明朗的。(Ashenfelter 等〔15〕〔16〕,以及 Dickinson 。〔17〕)
相关的文献从不同角度丰富和发展了FOA理论。但据作者所知,目前还没有专门文献从福利的角度研究FOA的结果。本文基于Brams和Merrill(1983;1986),第二部分给出了FOA下的纳什均衡必要条件和充分条件的一个直观表达,第三部分尝试从福利的角度评价FOA机制的结果。第四部分考察FOA在我国应用的可能性,结论部分给出了进一步拓展的方向。
二、模型
本文基于Farber(1980),假设有两个风险中性的参与人,仲裁者的偏好是共同知识①假定有参与人1与参与人2,一件事情是共同知识意味着,参与人1和2都知道这件事,1知道2知道,2知道1知道,1知道2知道1知道……,参见Aumann(1976)。,对仲裁者偏好的不确定性由一个连续的密度函数f来表示,且令其分布函数为F,F'=f。仲裁者偏好的中值为m,参与人1希望仲裁结果 (用数值表示)越大越好,参与人2希望越小越好,仲裁者选择离自己偏好方案最近的出价作为最终裁决。设二人的出价分别为b和α,f(m) >0,f'(m)存在,则参与人2的期望支付为:


判断 (a*,b*)是否为一个局部均衡出价,还需检验二阶条件:

从而可以得出参与人的一组出价为
这里,我们假设f'有定义。将 (a*,b*)代入二阶条件,有:
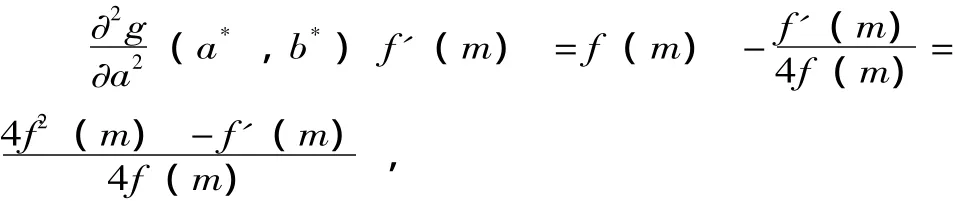
当且仅当f'(m)<4f2(m),取值大于0。
另一方面

当且仅当f'(m)>-4f2(m)时取值小于0。所以,我们有以下结论:(a*,b*)在丨f'(m)丨<4f2(m)时是一个FOA机制下的均衡出价。
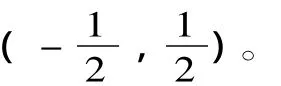


至此,我们完成了模型的解。直观上,我们可以在仲裁者的偏好服从正态分布时考虑上述条件。显然,当不确定性增加时,双方的最优叫价距离会更大。同样,当不确定性减小时,双方的最优叫价趋于接近。也许我们会认为,FOA既然不能为争端提供一个收敛的纳什均衡,那么,设计者的用意就没有被体现出来,从而其相较于CA来说,不能说具有优势。但在实践中我们却发现,FOA被大量应用。英国在上世纪90年代,很多劳动市场签订了应用FOA的协议。新西兰将FOA机制应用于警察补偿纠纷中,智利将这种制度引入水定价问题。纽约时报形容FOA机制在解决棒球大联盟球员的薪水问题上是一个巨大的成功。一个理论解释是,可能在这些问题上,仲裁者非常偏好中值点,双方参与人均意识到这一点,因而出价靠近。
三、一个简单的福利视角
从福利的角度,FOA能在多大程度上反映参与人的信息?我们采用完全信息下的仲裁作为一个比较基准①完全信息的假设相对严格,这里为方便说明问题采用此假设,不完全信息不改变本文的基本结论。。完全信息下,显然存在一个双方参与人的均衡出价,就是仲裁者的偏好方案,任何一方偏离这个唯一的均衡都不是效用最大化的选择。从这个角度,FOA的结果仅仅反映了一方参与人的信息。这是否是FOA至今没有在我国应用的一个原因呢?另一方面,在FOA机制下,一个方案只有在最接近仲裁者偏好的方案时才有可能被选中。这样,有可能出现一方出价的一个很小的变动(由于对仲裁者偏好的估计的改变,但在本文的模型中,仲裁者的偏好被假定为共同知识),就将使最终结果有很大的不同。
对于风险中性的参与人,我们也可以用双方的条件期望收益来衡量福利。根据 Samuelson(1991),FOA机制也可以被模型化为拍卖中的出价。令xi(i=1,2)为参与人i对仲裁者偏好f的估计,且f=0.5x2-0.5x1+μ,不失一般性,我们可以令μ=0。参与人的出价策略为b(·)和a(·),在一个对称均衡中,令a(x)=-b(x),定义b1=x1-b,b2=x2-a作为参与人的投标价,令B(x)=x-a(x),因为参与人i在B()内选择出价,故可令bi=B(z),视为参与人选择z。可以证明,参与i人的期望收益为P(xi,z)=[xi-B(z)]F(z) - ∫∞z[xj-B(xj)]f(xj)dxj。
应用包络定理:dPi/dxi=(∂Pi/∂z)(∂z/∂xi)+(∂Pi/∂xi),在均衡处, (∂Pi/∂z)=0,从而有=dPi/dxi=(∂Pi/∂xi)=F(xi)。
在完全信息下,参与人i的期望收益为:Pi(xi)=0.5xi-0.5E[xj] +μ,其中 μ 为仲裁者偏好的均值。
不难比较,在对偏好的估计值低于仲裁者偏好中值的估计情况下,dPi/dxi增加得比完全信息情况下要慢 (完全信息下,dPi/dxi=0.5),而当估计值高于中值时,dPi/dxi增加得比完全信息下要快。
如果从仲裁成本的角度来考虑福利问题,FOA的优势是显而易见的。因为它的实施只需要相对低的信息要求。在CA机制下,仲裁的实施要求对xi有精确的估计。在FOA下,仲裁者的任务只是选择一个相对更接近于f=0.5x2-0.5x1+μ的出价,而无需知道xi的精确值。而且,当参与人的分歧越大时,给定一个事先设置的正确选择水平,仲裁者可以在对x1的信息更少的情况下达到这个水平,这在实践中是有重要意义的。
四、最后要价仲裁可以应用于中国吗?
尽管FOA在国外得到了广泛的应用,但据笔者所知,国内还没有严格意义上的FOA在实际中的应用。张文运用最后要价仲裁模型对2001年国有股减持政策中的价格确定问题进行了对比分析,认为市场仲裁者缺乏独立的判断和决策权力是证券市场国有股减持失败的深层原因,因而有必要使市场监管和仲裁机构具有更大的独立性。〔18〕李小平考察了我国首次铁路春运价格听证的仲裁模型,认为价格听证获得成功的关键,在于价格听证中博弈双方对价格的呼声是否达到纳什均衡,价格听证需要从仲裁主体、仲裁程序等方面进行规范。〔19〕苑志勇、陈铁英、罗云锋描述了在双边电力市场中基于纳什均衡的竞价策略,认为问题的关键是找到纳什均衡,文章阐述了竞价策略的数学模型,并证明了纳什均衡的存在。〔20〕陈伟、王壬、周晓阳建立了双边电力市场中买卖双方报价的最后要价仲裁模型,认为应用FOA后市场交易员能较好控制电价,同时还可解决暗标拍卖所造成的价格波动。〔21〕郭勇、熊靖引入最后要价仲裁模型,从理论上考察了社区公共行政的博弈难题,认为由于现实中由于寻租现象的存在,FOA的均衡将难以达到。〔22〕
本文基于以上研究,提出一个房地产开发商与居民的博弈模型。开发商希望以较低的价格得到土地,居民希望得到较高的土地赔偿。假设存在一个双方都接受的仲裁者,并规定实行最后要价仲裁,理论上这会让开发商与居民更容易达成协议吗?如果参与人满足本文第二部分模型的假设,则结论依赖于仲裁者对其偏好函数中值点的偏好程度。参与人均衡情况下出价的差为:

不难看出,随着f(m)取值的增加,参与人出价将越来越靠近,即开发商与居民更有可能就征地补偿达成一致。进一步地,可以直观假设仲裁者的偏好服从正态分布来分析。若仲裁者的偏好方案服从N(m,σ2),其中m为均值,σ2是分布的方差,则密度函数可以写为:
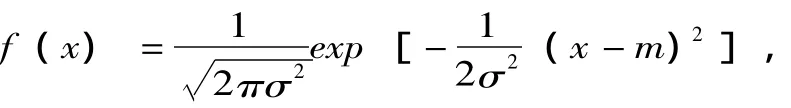
正态分布在均值两侧的分布是对称的,因而其中值等于其均值。从而,参与人均衡情况下的出价的差为:
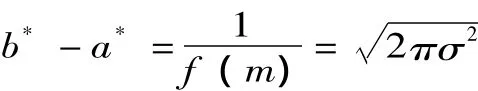
可以看出,要价之差随着参与人对仲裁者偏好方案的不确定性增大而增大。
这里,仲裁者的独立性是一个关键因素。在现实生活中,很容易想到让政府来充当仲裁者这个角色。如果政府的偏好波动性较小,且这个信息对于开发商与居民是共同知识,那么最后要价仲裁就是有效率的。近年常常见诸报端的拆迁矛盾,似乎也给最后要价仲裁留下了一片用武之地。
此结论要求仲裁者是完全独立的,而且其偏好分布对于参与者来说是共同知识。但正如一些文献提及的那样,政府往往有激励偏向某一方参与人。例如,地方政府可能会为了政绩考核,开发更多的房地产项目,拉动GDP,这样,政府便不再独立,因而最后要价仲裁的结论便不可靠了。基于独立性假设在实际中未必满足,考察当仲裁者系统偏向某一参与人时的均衡结果 (如果存在的话),便有了意义。这是本文可以拓展的方向之一。
五、结论与拓展的方向
分析不完全信息下的FOA机制实施问题,本文给出了均衡状态条件。在均衡条件下,FOA机制不能有效地促使参与人出价收敛,从而某种意义上不能实现设计者减轻激冷效应的意图。因为国内没有这方面的实证数据,所以只是给出了理论上的证明。但很显然,本文的假设条件是可以放松的,例如风险中性以及零和博弈的假设,这也是本文可以继续拓展的地方。另外,考虑参与人和仲裁者的关系,一个被称为乐观主义的假设是有道理的。即参与人都乐观地估计仲裁者的偏好分布中值更靠近己方的出价。针对实证的考虑,仲裁者是否系统地偏向于某一方参与人也是值得研究的。这一点,国外的FOA机制使用相对成熟,其经验值得我们借鉴。
〔1〕Stevens,C.M.Is Compulsory Arbitration Compatible with Bargaining?〔J〕.Industrial Relations,1966,5,38-52.
〔2〕Long,G.&Feuille,P.Final Offer Arbitration:“Sudden Death”in Eugene〔J〕.Industrial and Labor Relations Review,1974,27(2):186-203.
〔3〕Nelson,N.E.Final-Offer Arbitration:Some Problems〔J〕.Arbitration Journal,1975,30,50-58.
〔4〕Crawford V.P.On Compulsory-Arbitration Schemes〔J〕.Journal of Political Economy,1979,87(1):131-159.
〔5〕Farber,H.S.An Analysis of Final-Offer Arbitration〔J〕.Journal of Conflict Resolution,1980,24,683-705.
〔6〕Crawford,V.P.A Comment on Farber’s Analysis of Final-Offer Arbitration〔J〕.Journal of Conflict Resolution,1982,26(1),157-160.
〔7〕Brams,S.J.and Merrill S.Equilibrium Strategies for Final-Offer Arbitration:There Is No Median Convergence〔J〕.Management Science,1983,29(8),927-941.
〔8〕Brams,S.J.and Merrill S.Binding Versus Final-Offer Arbitration:A Combination Is Best〔J〕.Management Science,1986,32(10),1346-1355.
〔9〕Wittman,D.Final-Offer Arbitration〔J〕.Management Science,1986,32(12),1551-1561.
〔10〕Samuelson,W.F.Final-Offer Arbitration under Incomplete Information〔J〕.Management Science,1991,37(10),1234-1247.
〔11〕Hurley,W.J.Effects of Multiple Arbitrators on Final-Offer Arbitration Settlements〔J〕.European Journal of Operational Research,2003,145(3),660-664.
〔12〕Zeng,D.,Nakamura,S.and Ibaraki,T.Double-Offer Arbitration〔J〕.Mathematical Social Science,1996,31(3),147-170.
〔13〕Zeng,D.An Amendment to Final-Offer Arbitration〔J〕.Mathematical Social Sciences,2003,46(1),9-19.
〔14〕Zeng,D.How Powerful Is Arbitration Procedure AFOA? 〔J〕.International Review of Law and Economics,2006,26(2),227-240.
〔15〕Ashenfelter,O.and Bloom,D.Models of Arbitrator Behavior:Theory and Evidence〔J〕.American Economic Review,1984,74(1),111-125.
〔16〕Ashenfelter,O.,Currie J.,Farber H.S.& Spiegel M.An Experimental Comparison of Dispute Rates in Alternative Arbitration Systems〔J〕.Econometrica,1992,60(6),1407-1433.
〔17〕Dickinson,D.L.The Chilling Effect of Optimism:The Case of Final-Offer Arbitration〔J〕.The Journal of Socio-Economics,2006,35(1),17-30.
〔18〕张文.国有股减持与市场仲裁的独立性〔J〕.财贸研究,2002,(5).
〔19〕李小平.价格听证:仲裁模型与扩展解释-以我国首次铁路春运价格听证为例〔J〕.重庆工学院学报,2005,(6).
〔20〕苑志勇,陈铁英,罗云锋.基于Nash均衡的电力市场竞价策略分析〔J〕.华中科技大学学报 (自然科学版),2005,(1).
〔21〕陈伟,王壬,周晓阳.双边电力市场的最后要价仲裁模型〔J〕.水电能源科学,2006.(3).
〔22〕郭勇,熊靖.基于社区公共行政的博弈分析〔J〕.当代财经,2007,(5).
(责任编辑:王云川)
