变导程螺旋传动曲面建模与过渡螺旋线设计

张 威，史 翔，李东波

（1. 南京理工大学 机械工程学院，南京 210094；2. 南京工程大学 机械工程学院，南京 210094）

变导程螺旋传动曲面建模与过渡螺旋线设计

张 威1，史 翔2，李东波1

（1. 南京理工大学 机械工程学院，南京 210094；2. 南京工程大学 机械工程学院，南京 210094）

0 引言

传统丝杆只能进行不变导程的螺旋传动，丝杆的转动与螺母的直线运动保持严格的线性关系。为了使螺母运动速度达到设计人员的具体要求，只能通过对驱动丝杆电机进行转速的设计。即使这样，也不能精确满足螺母运动变化要求。在这样的情况下，变导程螺旋传动机构被提出，实现了丝杆转动与螺母平动的非线性关系，并且经过长期的试验和设计，目前在地铁上已经得到了初步应用。

在国内，对变导程螺旋传动副的研究只是刚刚起步，国外已经有学者对变导程螺旋传动进行了相关研究。Ming J. Tsai[1]对变导程螺旋传动机构的传动效率进行了评价分析。Yan 和Cheng[2]对传递滚子的曲面轮廓进行了相关研究。Chiou[3]研究了变导程螺旋传动的动态特性从理论上进行了分析。本文主要针对单滚子螺旋传动机构啮合曲面进行数学建模，并针对螺旋曲面进行设计。

1 螺旋面方程

在工业生产中，丝杠螺纹最常用的加工工艺是铣削加工，本节不考虑加工误差问题，而是把重点放在曲面形状。刀具沿着圆柱螺旋线移动过程和与其形状相同的滚子进行传动过程是相仿的。铣刀半径是不能忽略的，加工出的圆柱螺旋槽实际是不同直径的圆柱上螺旋线的径向排列，它们的导程相等，螺旋角不等，直径越大则螺旋角也越大。图1表示外螺旋线和内螺旋线螺旋升角的比较，N-N’是外螺旋线的法向截面。可以发下，只有外螺旋线与滚子外圆法向截面上相切，而内螺旋线由于其螺旋升角大于外圆螺旋线的，不会与滚子外圆在法向截面相切。这样螺旋槽的法向截型发生变形，即在N-N’截面上，螺旋槽型面上窄下宽。

这样，螺旋面的母线与丝杆轴线不相交，螺旋槽侧面不是正螺旋面。在丝杆坐标系中，Z轴为丝杆轴线，滚子圆周方向为X轴，XYZ符合右手螺旋法则。螺旋面的准线参数方程为：

因为铣刀与螺旋面外轮廓线相切，切点与丝杆轴线有一定偏移量，该偏移量为r·sin（λ），螺旋升角λ与螺旋线半径有关。则螺旋面母线参数方程为：

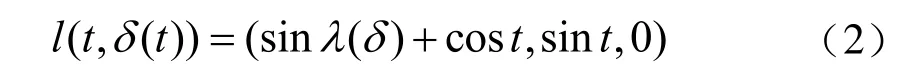
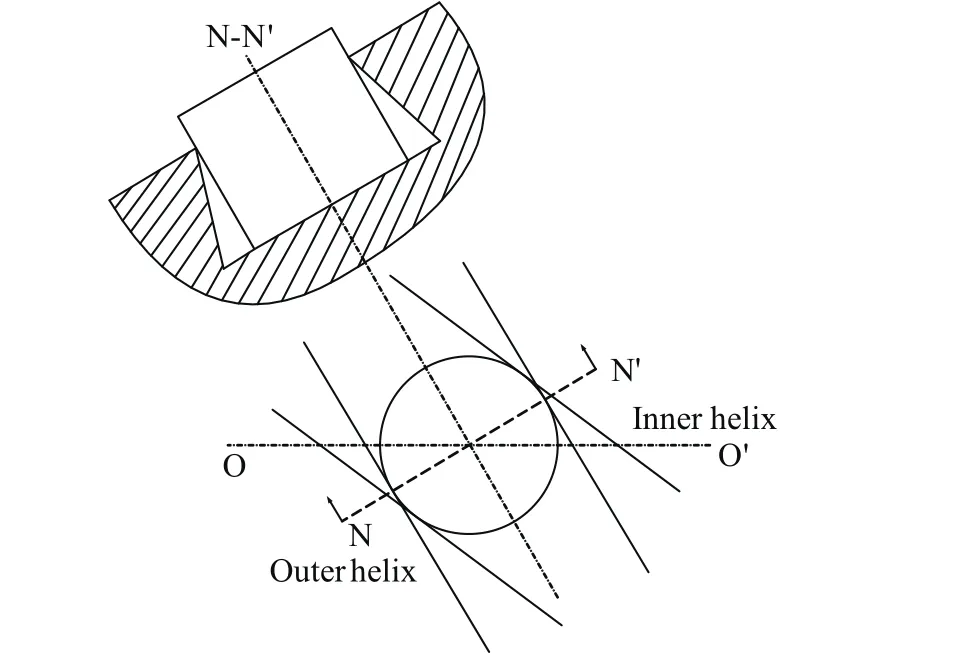
图1 螺旋槽剖面图

根据式（1）、式（2）得到螺旋槽侧面参数方程为：

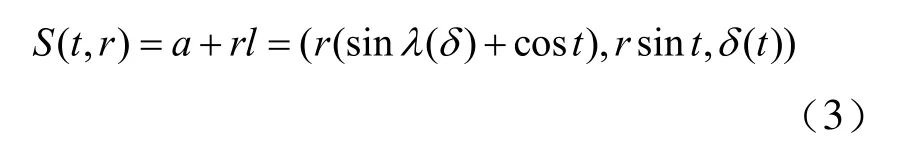
2 变半径变导程螺旋线数学模型

一般螺旋线的参数方程为：

其中，半径r和旋转角度f是轴向位移的函数。

螺旋线的螺旋特性可以由统一的螺旋参数来描述，即螺旋角和导程虽然二者概念不同，但描述螺旋线的同一特性。若考虑螺旋线的旋转半径，则表述了围绕任意旋转体的变导程螺旋线，螺旋线上任意点P坐标（r，θ，z），螺旋升角λ为z的函数。

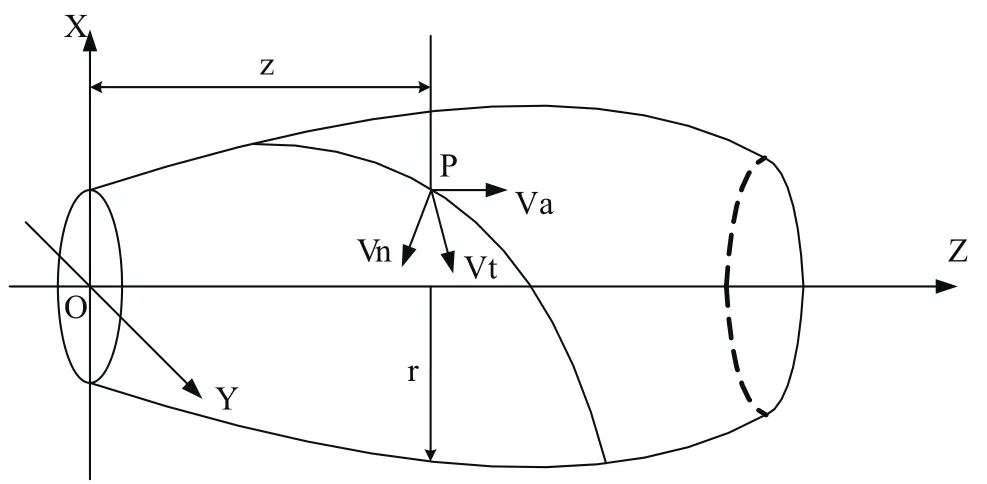
图2 变半径变导程螺旋线坐标系

如图2所示动点P为加工变导程螺旋槽刀具回转轴与旋转体母线的交点，其运动速度的三个分量分别为轴向速度VA，周向速度Vt，径向速度Vg。Vu=VA+ Vg表示沿P点处回转体母线切线方向速度。其中螺旋升角用速度分量表示为：

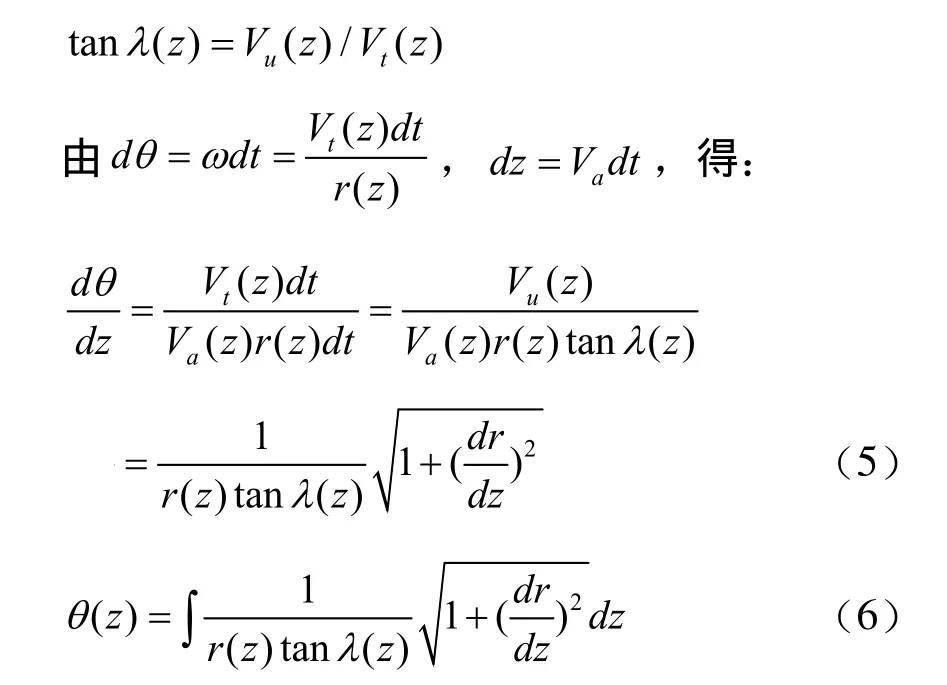
所以旋转体上螺旋线的局部形状由θ（z）、λ（z）和 r（z）完全描述。

螺旋线上任意一点坐标为：

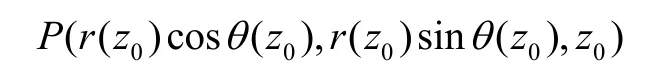
将z用θ表示，则变半径变导程螺旋线的参数方程为：

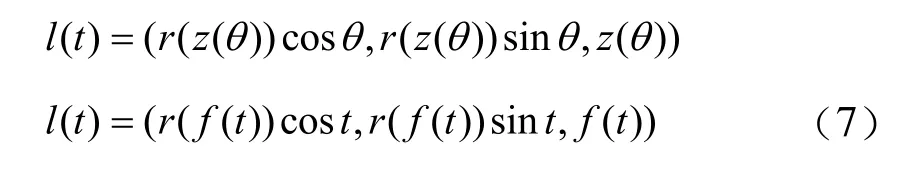
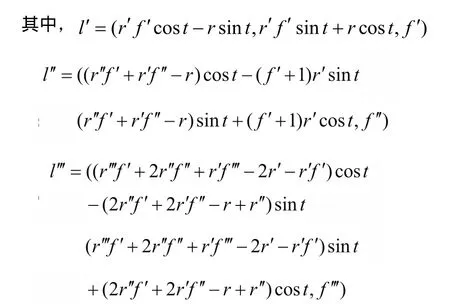
本论文研究对象是变导程螺旋传动中，滚子传动轨迹是圆柱螺旋线。当螺旋线的所在旋转曲面为圆柱面时，r为常数a。则函数f（t）表征了变导程轨迹。

由此，若f = f（t），则：

由此可知，给定任意常半径变导程螺旋线参

数方程l(t)= (ac osθ(t),as inθ(t),f(t))，其任一点

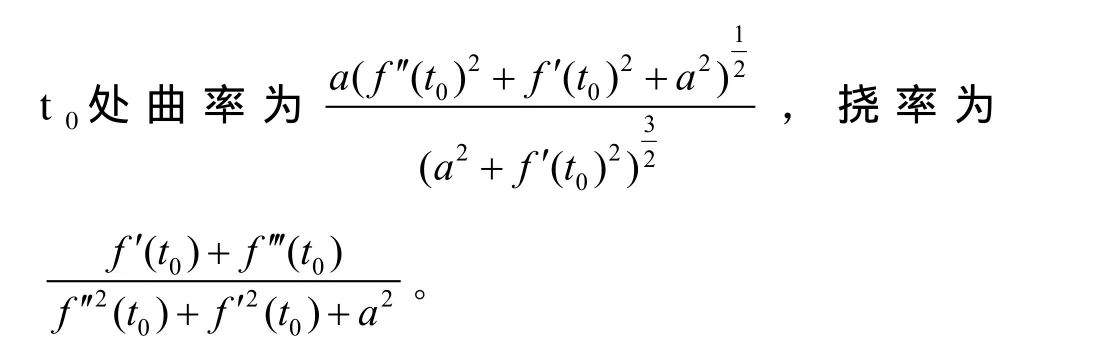
3 圆柱面过度曲线设计

3.1 圆过渡曲线设计

圆柱面上的过渡曲线需要满足在两个连接点处至少一阶连续，过渡圆能满足基本的过渡曲线要求，并且本身具有n阶连续特征。以下对圆柱面上两条常导程螺旋线进行圆过渡。

将圆柱面展开，并使曲线G以圆弧过渡连接曲线L1和L2，如图3所示。

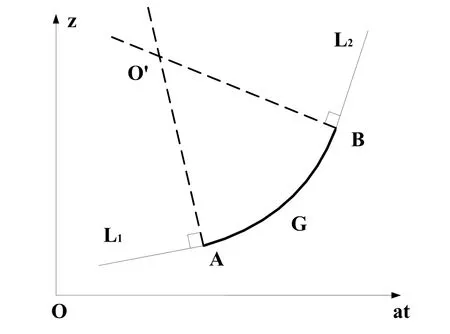
图3 圆过渡曲线

建立展开图中局部坐标系，A点坐标为A(atA,zA)，A点斜率为kA=pA/2πa；B点坐标为B(atB,zB)，B点斜率为kB=pB/2πa。易得O'点坐标为：

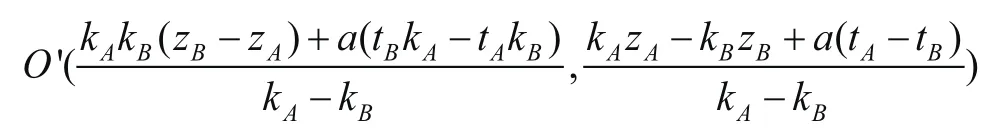
圆弧的曲率半径为：

则在全局坐标系下此圆柱面圆弧曲线方程为：

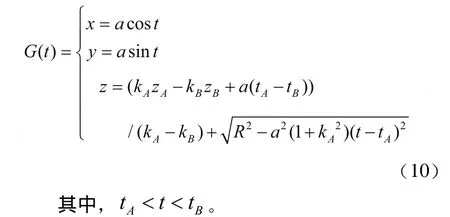
3.2 多项式曲线设计

如图4中，L1是导程为pA的螺旋线，L2是导程为pB的螺旋线，A为L1的端点，其坐标为(acostA,asintA,zA)；B为L2的端点，其坐标为(acostB,asintB,zB)。要求构造一条连接曲线L1，L2的光滑曲线G，使得曲线G分别与L1和L2在A点和B点相切。

图4 连接A、B两点的曲面族示意图

令曲线G参数方程为：

此时将空间曲线转化为平面曲线进行研究，得到了连接曲线L1和曲线L2的过渡曲线族G（t，β），β为曲线形状参数。原螺旋线的坐标转变成直角坐标Sxoy，这时的参数方程为：

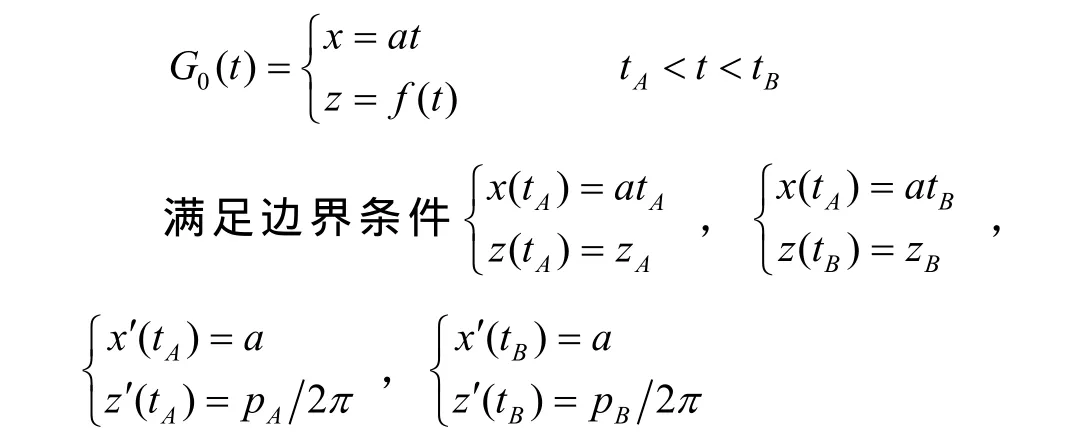
由于需满足四个边界条件，将函数z = f（t）定义为四次多项式函数：

其中，mt为待定系数，β为形状参数。

将边界条件分别代入方程（12），得线性方程组：

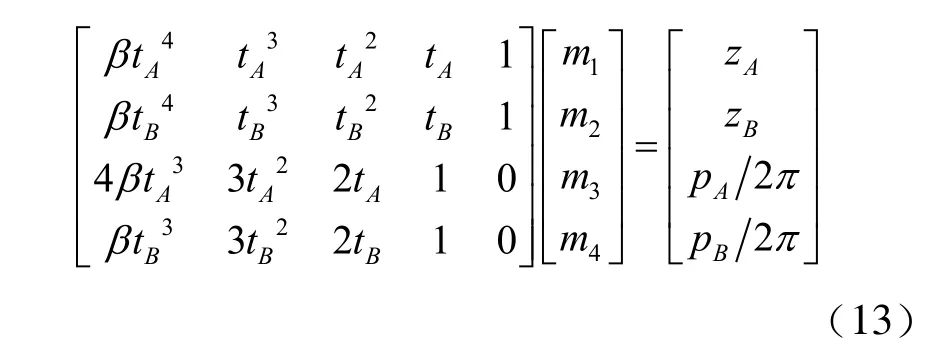
其中β决定了过渡曲线的性质。

[1]Ming J. Tsai；Jan-shiung Sun and Jan-chung Chu.Kinematic design optimization of the variable lead screw mechanism with cone meshing element. Mech. Mach.Theory

[2]J.Y. Liu；H. S. Yan. Surface geometry of variable pitch cylindrical cams with conical meshing elements. ASME Transactions,Jounal of Mechanical Design. 1994,116

[3]S. T. Chiou. Computer integrated design and manufacturing of varialbe pitch lead screw transmission mechanisms.Dynamic designs. 1993,Vol. 31

[4]萧仲敏. 复杂曲面CAM系统设计的研究[J]. 制造业自动化,2011,33(2).

[5]李和. 汽车曲面品质分析及光顺优化方法研究[J]. 制造业自动化,2011,33(2).

Surface modeling and transition helix design for variable lead screw transmission

ZHANG Wei1，SHI Xiang2，LI Dong-bo1

本文对变导程螺旋传动中螺旋面的通用曲面方程进行建模，建立了螺旋面的变半径变导程准线方程，并采用圆过渡和多项式曲线过渡两种方法对螺旋线即准线的过渡部分进行了设计。

变导程；螺旋传动；过渡螺旋线

张威（1982 -），男，河北唐山人，博士研究生，研究方向为机械电子工程。

TH391

A

1009-0134(2013)01(下)-0132-03

10.3969/j.issn.1009-0134.2013.01(下).38

2012-09-13