离散突变－模糊物元法在水路运输组织评价中的应用

辛曼玉

(东莞职业技术学院物流工程系，广东东莞 523808)

0 引言

随着我国产业结构的不断升级和临港物流园区的快速推进，地方经济发展对港口货物运输的依存度不断提升.作为现代港口物流中的重要环节，水路运输组织方案选择的合适与否是提高货物运输效率、降低企业运输成本的重要手段.［1］在面临良好发展机遇的同时，国内物流企业在降低运输成本和提高运输效率上也面临着诸多挑战.因此，进行运输组织评价、选择合适的运输组织方案，对物流企业提高综合竞争力有着重要的作用.

水路运输具有运量大、能耗低、成本低等特点.近年来，我国水运行业不断发展，在综合运输体系中的地位不断提升，国内关于水路运输组织方式的研究也不断深入.目前，国内学者常用人工神经网络等方法对水路运输组织方式进行评价［2］，水路运输组织方式评价存在指标繁多、权重确定难等特点，传统方法在评价的客观性、可靠性上还有待进一步提升.

针对国内水路运输发展的特点，结合数据的可得性，本文从技术性、经济性和社会效益等3方面建立评价指标体系，并运用离散突变－模糊物元法建立评价模型，有效克服各种方法的局限性，增加评价结果的客观性，为水路运输组织方式的评价提供新的思路［3］.

1 离散突变－模糊物元评价模型概述

1.1 传统评价方法概述

当前，国内外学者已针对运输组织方式评价提出的方法有神经网络法、数据包络评价法、模糊综合评价法等.表1对传统评价方法进行概述和优缺点评价.

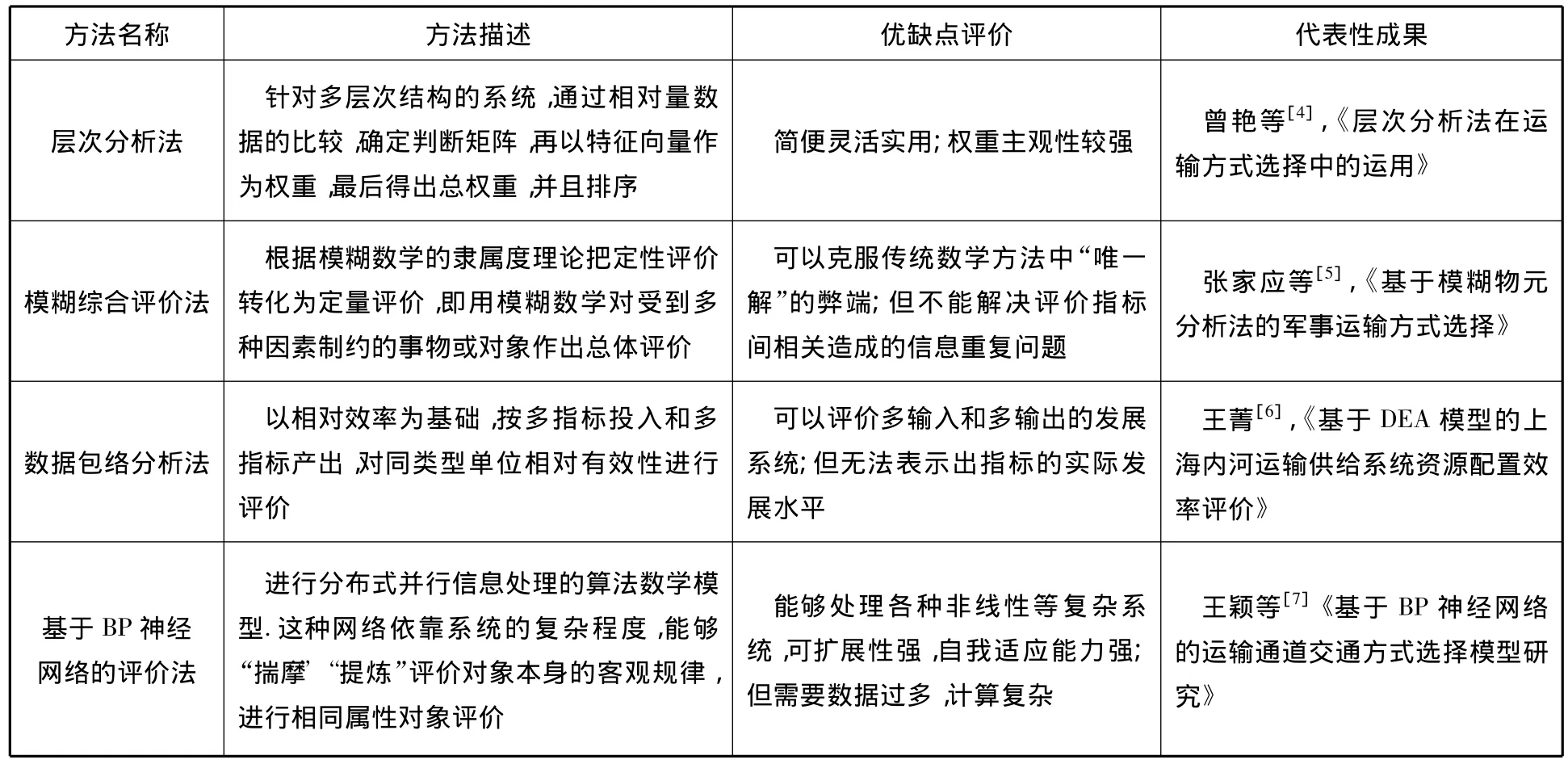
表1 传统评价方法综述

通过以上分析可以看出，层次分析法、模糊综合评价法和数据包络分析法在进行运输方式选择评价时存在着权重取值主观性较强、评价指标信息重复等问题，评价结论的客观性和可靠性难以得到较好保证;神经网络法虽能解决复杂的非线性问题，但对数据量依赖较大，计算也较为复杂，难以实施.

相对传统方法研究该问题的局限性，离散突变－模糊物元法兼顾多种评价方法的优点，能有效提升水路运输组织方式评价研究的客观性和可靠性［8］.在处理数据时所使用的模糊物元法［9］能客观分析指标关系间的模糊性，揭示指标的特征和相互间的联系;通过评价指标体系的分层次，突变评价法阐释评价指标间的上下层隶属关系，以及同层指标的独立性与相关性，并简化计算过程;此外，在突变评价法中引入离散系数法，可以避免评价过程中对同层指标相互关系间的主观判断，保证评价结论的客观性.

1.2 离散突变-模糊物元模型构建

1.2.1 构建模糊物元

根据模糊物元的定义［10］，若待评价的方案有n个指标 C1，C2，…，Cn，与其相应的模糊量值分别为u(r1)，u(r2)，…，u(rn)，则称 R 为 n维模糊物元.若以Rmn表示m个评价样本的n维复合模糊物元，并以Mi表示第i个评价样本，Cj表示第i个样本的第j项评价指标，与其相应的模糊量值为u(rij)(i=1，2，…，m;j=1，2，…，n)，则有:

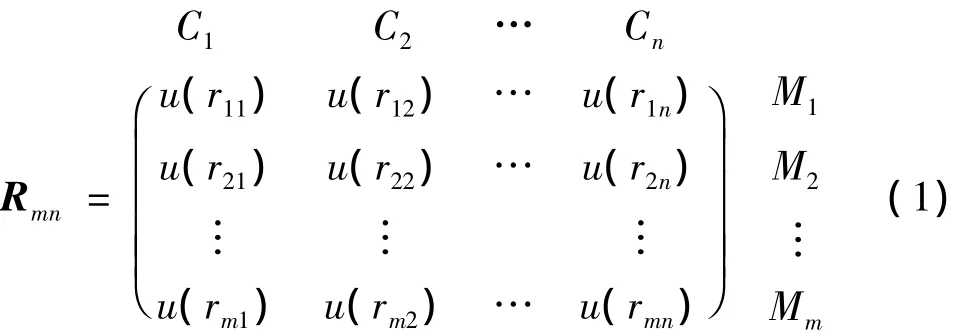
1.2.2 从优隶属度及其准则

由于n个评价指标的含义和计算方法不同，以至于它们的量纲各异.应先对n个评价指标计算值进行标准化处理，即将决策矩阵进行标准化处理.令J+={越大越好的指标}，J－={越小越好的指标}.则有:

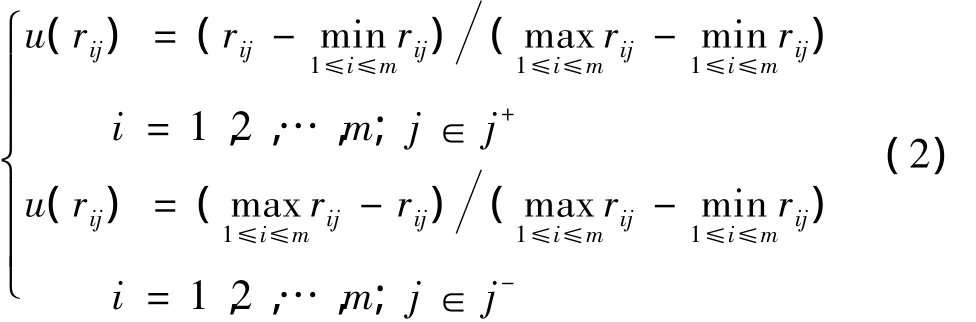
式中:rij为第i个方案第j项指标对应的量值;max rij和min rij分别为各评价方案每一项评价指标所有量值rij中的最大值和最小值.

1.2.3 标准模糊物元与差平方复合模糊物元计算

由式(2)可以构造标准样本n维模糊物元Rin，其中各项由Rmn内各评价样本从优隶属度中的最大值或最小值加以确定，则可得

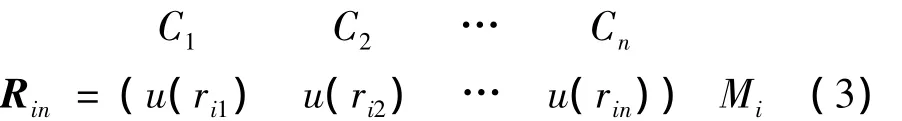
若以 Δij(i=1，2，…，m;j=1，2，…，n)为元素组成的矩阵表示标准模糊物元Rin与复合模糊物元Rmn中各项差的平方，则组成差平方复合模糊物元

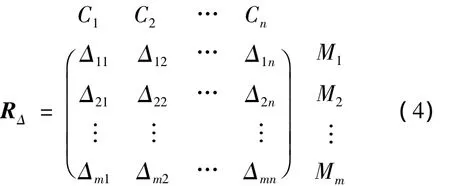
式中:Δij=(u(r0i)－u(rij))2(i=1，2，…，m;j=1，2，…，n)

1.2.4 突变评价

在对基础数据即物元进行相关处理后，选用基于离散系数的突变评价法进行评价.突变评价法即对评价目标进行多层次矛盾分解，然后利用突变模糊势函数，再由归一公式量化运算，最后得到一个参数，即计算出总的隶属函数，从而对评价目标进行排序比较的一种评价方法.

传统的突变理论在进行模糊评价时，一般会考虑两个原则，即“互补”和“取舍”原则.若同一对象各控制变量(如a，b，c，d等)之间不存在明显的相互关联作用，则称该对象各控制变量为“非互补”型，否则称该对象各控制变量为“互补”型.对于“非互补”型的指标，按“大中取小”的取舍原则取值，即取控制变量相应的突变评价值.如果存在“互补性”，则按“平均取值”的互补原则取值.但为了得到更精确的结果，本文在传统的两大原则基础上，引进离散(突变)系数法［11］，是根据各个指标在所有被评价对象上数据值的离散程度大小对其赋权.具体方法如下:

分别求出第j个指标标准化值的平均值b0j和标准差 σj，即

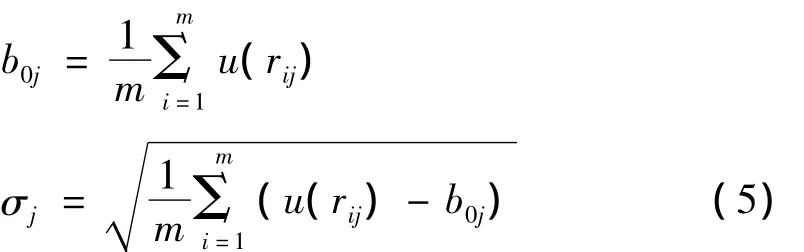
则第j项指标标准化值的离散系数［12］

因此，第j个评价指标的权重

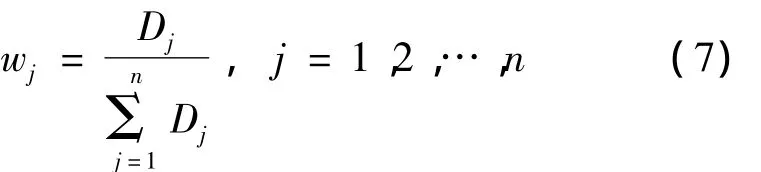
即n个评价指标的权重向量

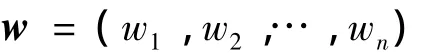
将方案的总决策作为状态变量，将每个次级指标决策值作为控制变量，并采用突变模型对各方案的上层决策值进行测算.假设次级指标以下有n个3 级指标，令 G=(G1，G2，…，Gn)表示为次级指标的决策值，结合以上模糊物元模型，则假设第一个次级指标下面有3个3级指标，为 C1，C2，C3.则

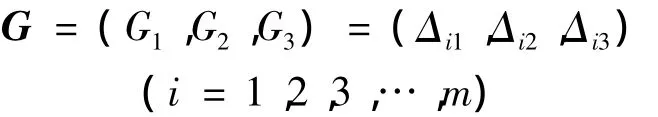
突变测算后可得到3种归一公式.其中，燕尾模型公式为

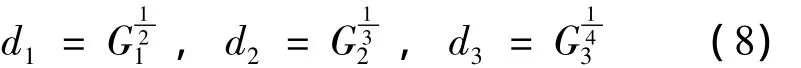
结合以上理论，以3层指标体系和燕尾突变模型为例，则方案突变决策系统评价的步骤:

(1)运用离散系数法，求出第3层指标中各个指标占整个体系的权重，以求得指标体系第2层指标，即次层指标占整个体系的权重，并按权重从大到小的顺序对次级指标下辖的第3层指标进行排序，依次对应排列综合决策值，得出新的决策向量Gk=(Gk1，Gk2，Gk3)(k=1，2，3，…，n).

(2)运用燕尾突变模型归一公式，对Gk进行计算，即

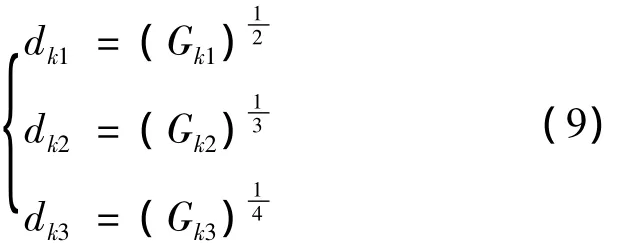
从而得出次级指标的决策分隶属度向量

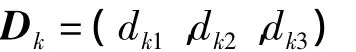
(3)对燕尾归一模型所得值，按互补原则计算，可得k方案的整体综合决策值.在评价指标体系的下层中，可以通过重加权的方式求出某一指标在其所属下层指标体系中的局部权重.即

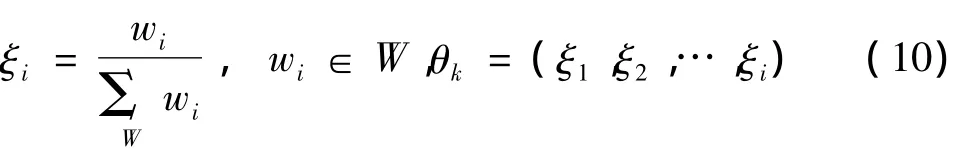
运用局部权重对次级指标的决策分隶属度向量进行加权计算，求得次级指标的突变隶属度值，即

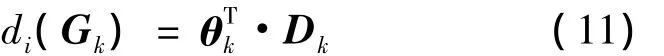
重复前3步，运用次级指标的突变隶属度值，根据次级指标占整个指标体系的权重，计算指标体系最上层的隶属度值，即方案的隶属度值di.

1.2.5 综合评价

贴近度是指被评价样品与标准样品两者互相接近的程度，其值越大表示两者越接近，反之则相离较远［13］.因此，可以依据贴近度的大小对各方案进行优劣排序，也可根据标准值的贴近度进行类别划分.考虑到本文的具体评价意义，通过采用欧氏距离法计算贴近度，并令RP为贴近度复合模糊物元.

各方案的贴近度值:

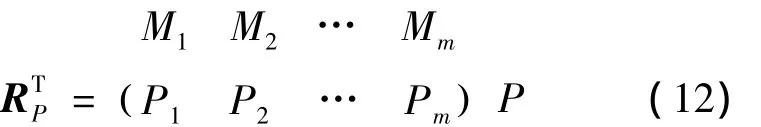
通过上文基于离散系数的突变级数法所得出的隶属度值di，可以得出Pi的值，从而可以得到方案的优劣排序.

2 运输组织评价指标体系的建立与分析

水路运输组织方案的综合评价属于多指标评价.在多指标综合评价体系中，指标体系的建立是进行评价的前提条件.要对评价对象进行系统性分析，找出影响评价对象优劣水平的各相关因素，在参考有关资料和专家意见［14］的基础上加以归纳整理，得到水路运输组织方案综合效益评价指标体系，见表2.

由表2中的指标体系可见，技术性指标B1之下的3个2级指标C1，C2，C3构成燕尾突变，则应先计算xC1，xC2，xC3，再计算其局部权重，并对之进行加权，从而得到B1的隶属度值xB1.同理，经济性指标B2之下的 4 个 2 级指标 C4，C5，C6，C7构成蝴蝶突变，社会效益指标B3之下3个2级指标C8，C9，C10构成燕尾突变.在分别计算其隶属度值之后，3个1级指标构成燕尾突变，由此可求出方案的突变隶属度结果.

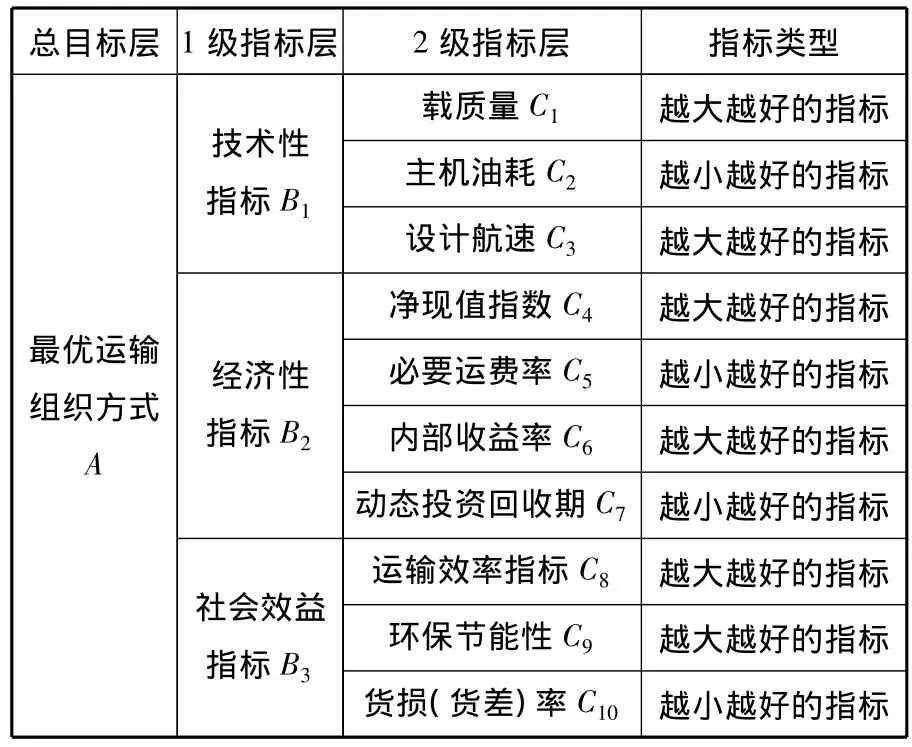
表2 多层次指标体系

3 应用实例

下面以广西红水河能源水路运输组织方式的选择为实例，利用离散突变－模糊物元评价法分别对各运输组织方式进行评价，从而选出最优的组织方式.红水河水运组织方式主要有3种:(1)水路直运完成运输量500万t，可采用500吨级、1 000吨级船舶运输;(2)公路、水路联运完成运输量300万t，可采用300万吨级船舶运输;(3)滚装船舶运输完成运输量300万t以上，可采用40车位和60车位滚装船运输.综合考虑船型和运输方式，把300吨级水路直运、500吨级散货联运、1 000吨级散货联运、40车位滚装船运输、60车位滚装船运输这5个运输方案分别定义为 M1，M2，M3，M4，M5.

在对以上3种方式5种船型的各指标数据用式(2)进行归一化的基础上，运用离散系数计算式(5)～(7)求出各指标权重和局部权重，见表3.

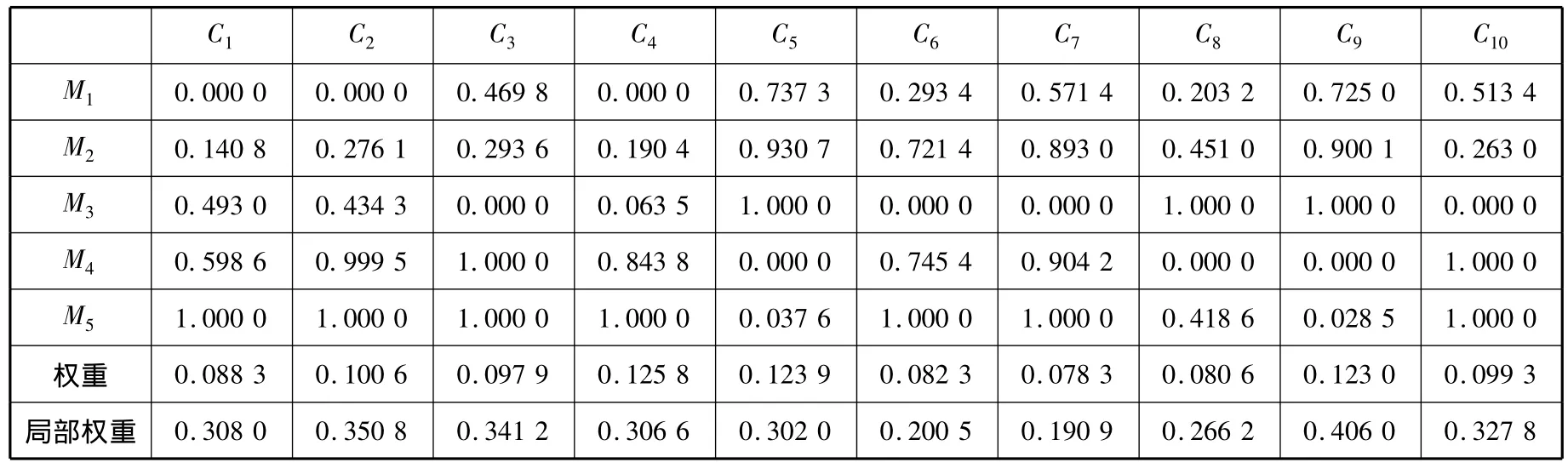
表3 各方案从优隶属度和各指标权重

利用式(3)～(4)，根据标准模糊物元和Rmn构 建差平方复合模糊物元RΔ，见表4.

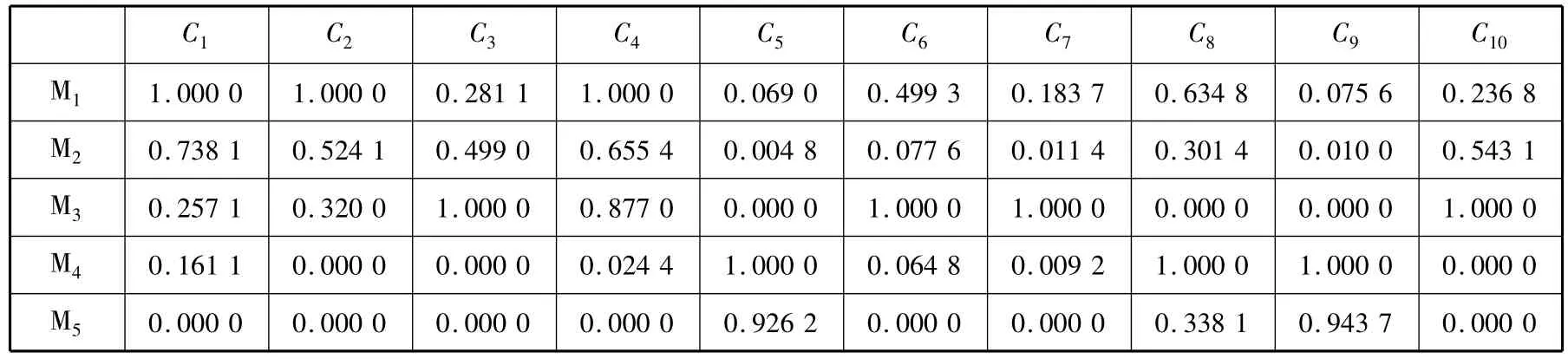
表4 差平方复合模糊物元RΔ

再用离散突变评价法计算各方案的突变隶属度.下文以方案M1为例，介绍其具体操作.

首先，技术性指标B1之下的3个2级指标C1，C2，C3构成燕尾突变，而由表3可知，在3个指标的权重中，w(C2)＞w(C3)＞w(C1)，在指标重要性上的排列为C2，C3，C1，以此对应燕尾突变归一化的隶属度 X=(xC2，xC3，xC1).因此，同理，可求得方案M1所有1级指标的隶属度值为

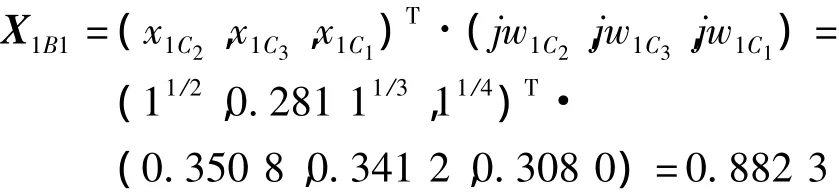
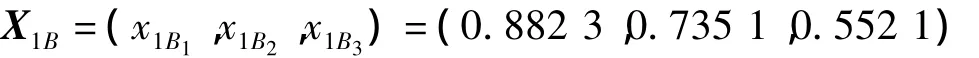
根据表3中通过对1级指标下属2级指标的权重累加可计算出1级指标的权重

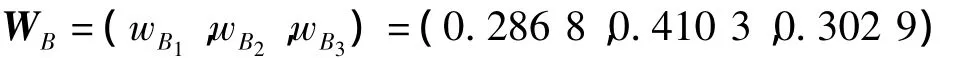
由前文中的分析可知，3个1级指标构成燕尾突变，而从权重中可见w(B2)＞w(B3)＞w(B1)，在指标重要性上的排列为C2，C3，C1，以此对应燕尾突变归一化的隶属度X=(xC2，xC3，xC1).因此，

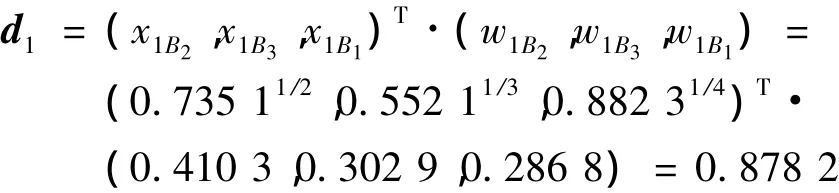
即方案M1的突变隶属度为0.878 2.

同理，可以求出其他方案的突变隶属度，并利用式(15)求得所有方案的贴近度，见表5.

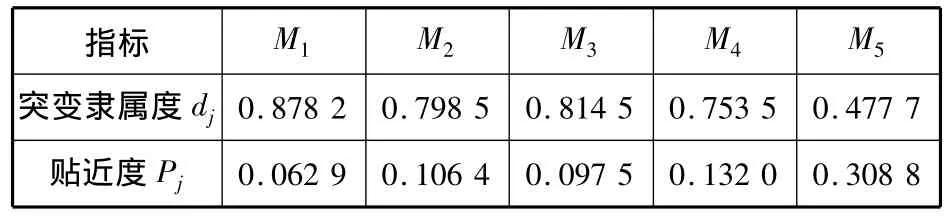
表5 方案的突变隶属度和贴近度

按照贴近度从大到小排序依次为:采用60车位滚装船运输(M5)、40车位滚装船运输(M4)、500吨级散货联运(M2)、1 000吨级散货联运(M3)、300吨级水路直运(M1).M5是最优方案.

此外，本文用其他方法对该案例进行评价，其评价结论以及与本文中运用方法的对比见表6.

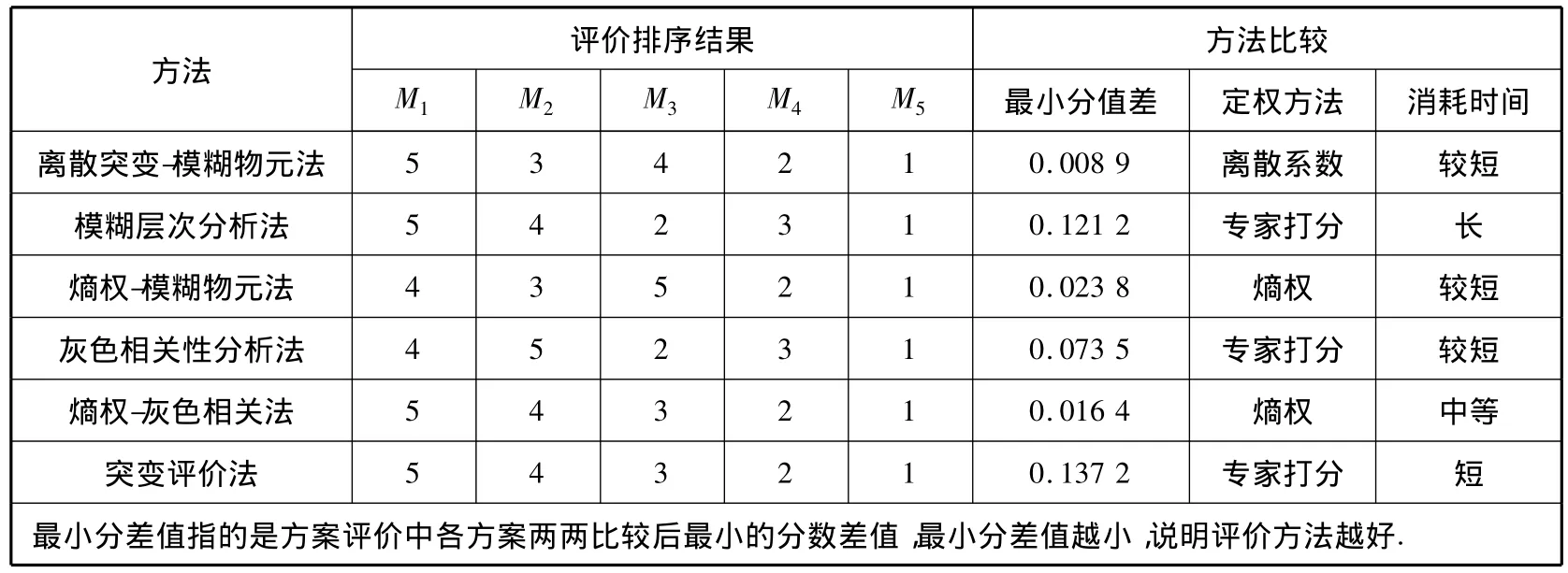
表6 主要评价法的评价排序结果与方法对比

以上结果表明:离散突变－模糊物元法的计算结果与其他常用评价法基本相符，但该方法的最小分值差远小于其他评价方法，说明该方法评价结果较为精确;计算过程耗时较短，表明该方法计算十分简便，应用性较强.因此，该方法对水路运输组织方法的评价选择具有较好的适用性.

4 结束语

内河水路运输是“十二五”期间我国综合交通运输体系建设的重点所在.运输方式如何选择、如何组合是当前交通运输组织的热点和难点.针对水路运输组织方式评价的特点，本文引入基于离散系数的突变评价法，并基于模糊物元分析，根据经济性、技术性、社会性等3方面的评价指标体系，构建离散突变－模糊物元评价模型.通过实例论证，该方法计算简便、结论合理，能提高水路运输组织方式评价的客观性和科学性，并具有较高的实用性.

［1］刘铁鑫.面向复杂货流的综合运输组织方式优化研究［D］.武汉:武汉理工大学，2010.

［2］周丽丽，胡甚平.船舶引航风险成因灰色综合评价模型［J］.上海海事大学学报，2008，29(3):21－25.

［3］朱秋子.长三角公路水路运输一体化保障机制研究［D］.上海:上海海事大学，2007:41－43.

［4］曾艳，余治平，李映红.层次分析法在运输方式选择中的运用［J］.交通标准化，2005(12):14－17.

［5］张家应，鲁凯，吕游.基于模糊物元分析法的军事运输方式选择［J］.国防交通工程与技术，2008(5):67－70.

［6］王菁.基于DEA模型的上海内河运输供给系统资源配置效率评价［J］.物流科技，2010(4):59－62.

［7］王颖，邵春福.基于BP神经网络的运输通道交通方式选择模型研究［J］.物流技术，2010(12):59－62.

［8］万金保，朱邦辉.物元模型在庐山风景名胜区水环境质量评价中的应用［J］.安徽农业科学，2010(6):102－104.

［9］李振福，杨忠振.模糊可拓层次分析法研究［J］.上海海事大学学报，2006，27(3):71－75.

［10］邓丽华.多目标决策中的突变理论方法研究［J］.科技信息:学术研究，2007(21):54－57.

［11］胡启洲，陆化普.基于关联熵与复合物元的公交系统综合测度模型［J］.系统工程理论与实践，2011(1):186－192.

［12］张文青，胡甚平，刘琨，等.基于熵权的海上交通风险成因物元评价模型［J］.上海海事大学学报，2010，31(2):18－27.

［13］李伟，胡甚平，尤庆华，等.港口水域通航风险评价的未确知测度模型［J］.上海海事大学学报，2009，30(3):13－21.

［14］RAFTOYIANNIS I G，CONSTANTAKOPOULOS T G，MICHALTSOS G T，et al.Dynamic buckling of a simple geometrically imperfect frame using catastrophe theory［J］.Int J Mech Sci，2006(48):1021－1030.