带随机排序的进化策略法在电力系统无功优化中的应用

冯兴明

（河海大学能源与电气学院，江苏南京 211100）

无功优化是保证电力系统安全、经济运行的一项有效手段，合理的无功分布可以提高系统电压质量和降低电网损耗。

电力系统无功优化是指在系统有功潮流分布确定的情况下，通过对某些控制变量的优化调节，在满足系统各种约束条件的前提下使系统有功网损最小，它是一个带有多约束条件的非线性组合优化问题[1]。迄今为止，国内外学者对电力系统无功优化进行了大量研究[2-6]，已有多种方法可用于无功优化的求解，如非线性规划法、线性规划法、动态规划法和混合整数法等，但是这些方法都普遍存在对初始解的特殊要求以及不便于对离散变量进行处理等缺陷。

进化策略[7-8]（Evolution Strategy，ES）是由德国科学家I.Rechenberg和H.P.Schwefel于20世纪60年代提出，用于解决多参数优化问题。该方法具有全局收敛性、并行处理特性、通用性及强鲁棒性等优点，在解决多变量、非线性、不连续、多约束的问题时显示出独特的优势，在无功优化领域中的应用日益为人们所重视。惩罚函数法[9-11]是进化算法求解约束问题最常用的方法，但其惩罚系数难以合理确定，需要多次试验不断调整。

本文在前人研究的基础上，将带排序策略的进化策略法应用于电力系统无功优化，有效地避免了罚函数法处理约束问题时罚系数难以确定的缺点，并在编码方法、进化终止判据方面做了改进，有效地提高了无功优化的求解效率。

1 无功优化的数学模型

无功优化的目的是使整个网络的损耗最小，并提高电压质量，节约系统运行费用，使系统稳定安全运行，其数学模型包括目标函数和约束条件。

1.1 目标函数

本文采用的目标函数为系统有功网损最小，同时将状态变量（节点电压和发电机机无功出力）写成罚函数形式：

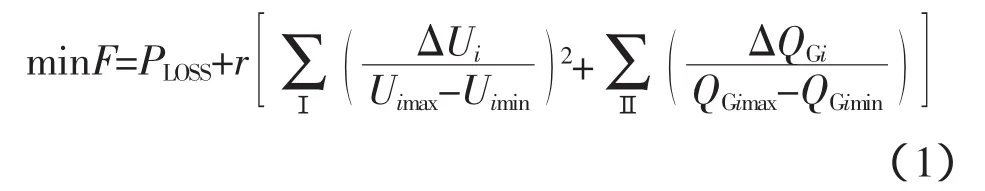
式中，右端第1项为有功网损；第2项为对节点电压幅值越限和发电机无功出力越限的惩罚项；r为罚函数的越限罚因子；I为系统PQ节点的集合；Ⅱ是发电机节点的集合。式中：

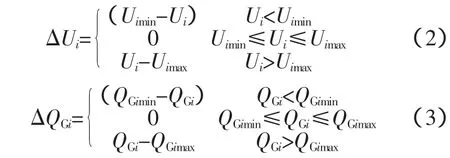
1.2 约束条件

等式约束为节点功率平衡方程式：

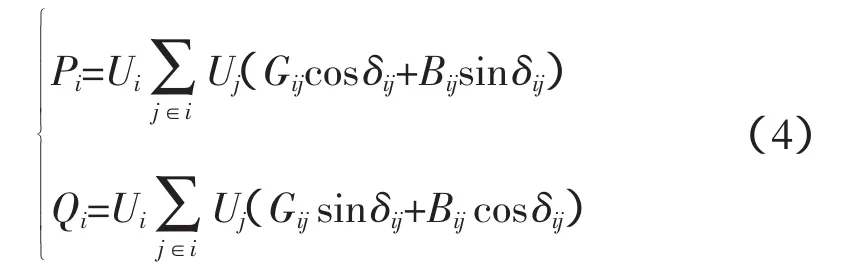
式中，Pi、Qi为节点i处注入的有功、无功；Ui，Uj为节点i，j的电压幅值；Gij、Bij、δij分别为节点i、j之间的电导、电纳和电压相角差。

控制变量约束方程：

状态变量约束方程：

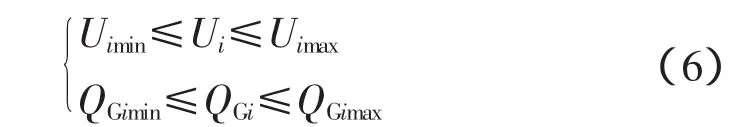
式中，TK为可调变压器分接头位置；QCi为容性无功补偿容量；UGi为发电机机端电压；Ui为节点电压；QGi为发电机无功出力。

2 改进进化策略法的无功优化

2.1 随机排序策略

惩罚函数法试图在目标函数和惩罚项中找到一个好的平衡，文献[12]在对目标函数值和约束违反程度关系分析的基础上，提出了随机排序的方法，很好地平衡了目标函数和罚函数，克服了惩罚系数难以选取的难题。算法采用了参数Pf表示在不可行区域中仅适用目标函数比较个体的概率，即当比较两个相邻个体时，若两个个体都是可行解，则比较他们的目标函数的概率为1，否则参数Pf将决定是否采用目标函数或约束违反程度来比较个体。

随机排序策略如图1所示。图中，N表示群体规模，u表示产生的满足一致分布随机数，Pf表示随机排序概率，Ij表示进化个体，准（Ij）表示个体j的罚函数值，f（If）表示个体j的目标函数值，Swap（Ij，Ij+1）表示交换相邻个体Ij和个体Ij+1。

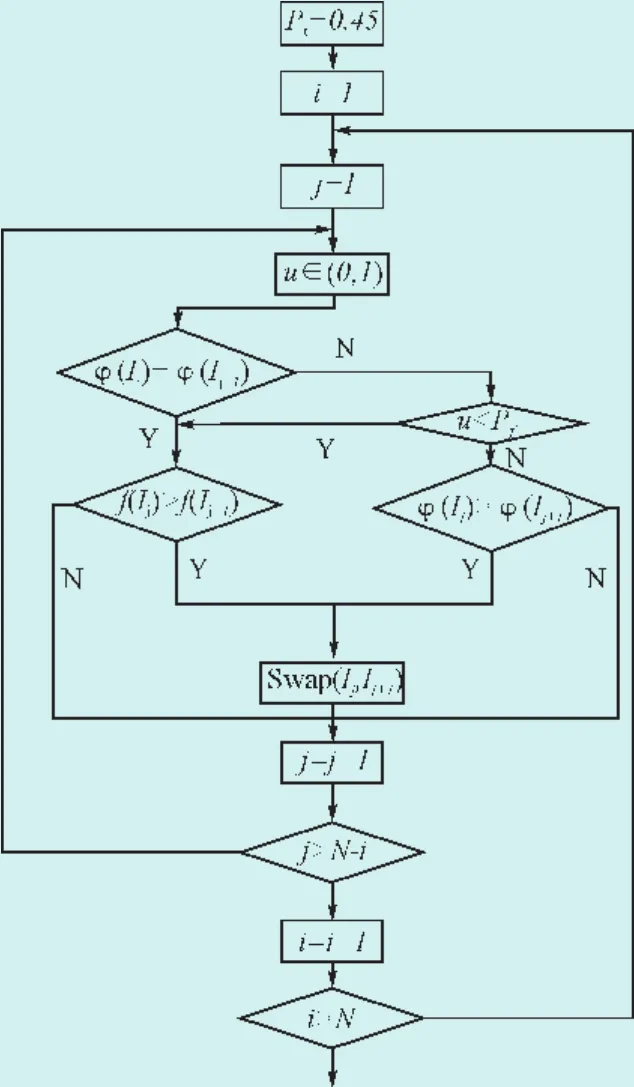
图1 随机排序策略Fig.1 The strategy of stochastic ranking

2.2 带随机排序的ES算法

本文采用（μ，λ）-ES进化策略算法进行无功优化，改进措施和算法流程如下：

1）编码

本文采用二元表达方式，开始时采用随机的方法给出λ个个体的一代，其取值在各自范围内，均值取某运行方式下的潮流解。

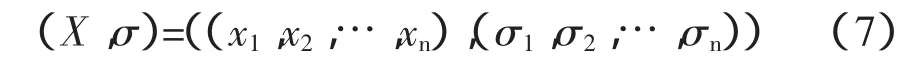
式中，X=[T，C，Ug]，T、C为变压器分接头和电容器组数，为整型变量；Ug为发电机机端电压，为实型变量。

2）变异

由随机排序策略对初始群体进行排序，选出μ个最好的个体作为下一代的个体，截断水平μ/λ≈1/7。随后从μ个老个体中产生λ个新的策略参数，平均步长按照log-normal更新规则更新：

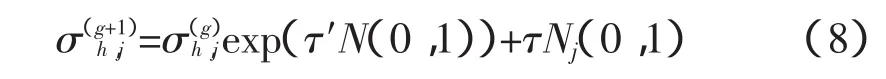
式中，h=1，…，λ；j=1，…，n，N（0，1）是服从标准正态分布的随机变量；Nj（0，1）表示为每个j的值重新生成随机数。“学习速率”τ和τ′分别设置成和是收敛的期望率。

在应用更新规则之前进行自适应参数的重组，尤其是两个父母之间的全局中间重组（平均）采用如下实施：

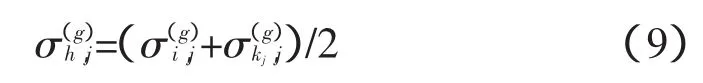
式中，kj是为每个j随机产生和更新的指数，kj∈{1，…，μ}。

改变了策略参数之后，每个个体（xi，σi），平均创造λ/μ个后代，这样就总共产生了λ个后代。

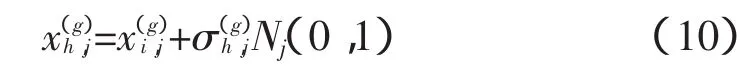
为保证优化能收敛，步长σ会越来越小，若对变异后的整型变量直接取整，将导致陷入局部最优，本文采用加0.5再取整。

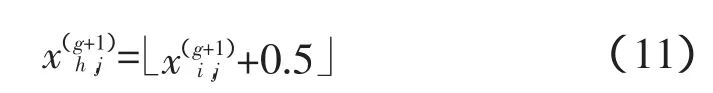
3）选择

按照公式（1）分别计算个体适应函数值和罚函数值，并依据本文2.1给出的随机排序策略对个体进行排序，从λ个个体中选择前μ个进入下一代。

4）终止

将目标函数值和优化控制变量的变化程度作为优化终止判据，预设一可配置变换的阈值，计算连续若干代目标函数和优化控制变量的方差，若方差小于阈值，可推断算法已收敛，提前终止优化进程。本文采用最大进化代数和优化终止判据相结合的方法来判断是否终止优化过程。

2.3 算法流程

算法流程见图2。

3 算例分析

为了验证本文改进算法的优化效果，用C++编程对IEEE-14和IEEE-118节点系统进行优化，系统的接线图和原始数据可参考文献[15-16]，基准功率取100 MVA。

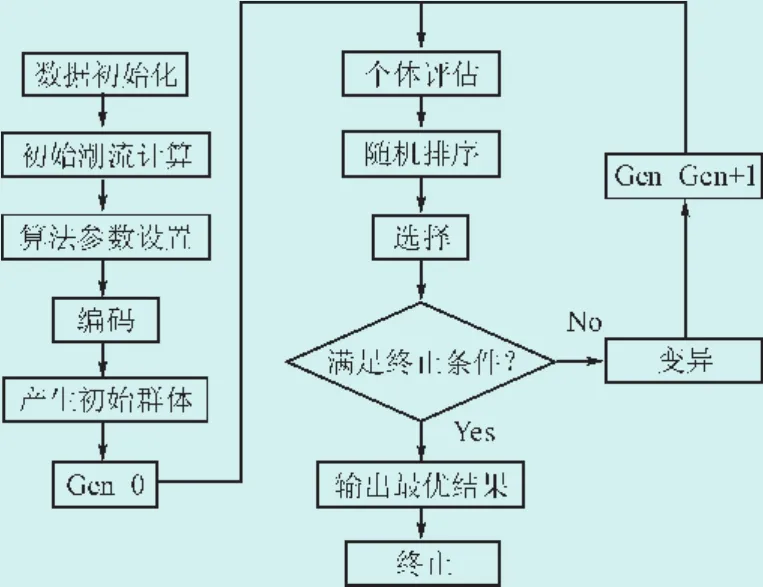
图2 算法流程Fig.2 Flow chart of ES with stochastic ranking

IEEE-14系统中共有5台发电机，机端电压连续可调。3台变压器，其变比调节范围[0.9，1.1]，共有9档分接头，调节步长2.5%。各节点电压上下限为[0.95，1.05]（标幺值，下同）。节点9装有无功补偿装置，分5档投切，步长为0.1，其补偿上限为0.5（标幺值）。初始系统的有功损耗为0.138。

IEEE-118节点系统，共有118个节点，186条支路，54台发电机，14个无功补偿节点，其中69号为平衡节点。变量变化范围如表1所示。进行算法测试之前，先配置相关参数，具体如表2。

方差用来做进化终止判据，当连续计算目标函数值的次数达到方差计算代数（本文取值20）时，且这连续20次目标函数的方差不大于方差（本文取值0.000 1），则终止进化；若不满足方差条件，则进化到300代终止进化过程。

表1 变量变化范围Tab.1 The range of variables

表2 算法参数设置Tab.2 Algorithm parameters setting

表中μ表示父代个体，λ表示子代个体，Pf表示比较概率，Emax为最大进化代数，Efcds为方差计算代数。

由于本文采用随机的概率搜索技术，随机数不同时初始量不同，计算结果也不同。算法优化后14节点和118节点系统网损值比初始值降低了4.43%和4.3%，如表3分别为30次计算结果的统计值；表4比较了在ES算法中分别使用随机排序策略、恒定罚系数、线性罚系数和指数罚系数下网损情况。结果表明，处理约束问题的效果和罚系数的处理方式有关，合理设置罚系数十分复杂，随机排序的方法在避免了罚系数难以选取的同时，仍能保证较好的优化效果。

表3中网损方差值仅为0.000 004和0.000 057，体现了算法的收敛稳定性，而图3表明算法能在稳定的进化代数内收敛。从计算时间来看，本文提出的基于随机排序的进化策略方法（SR-ES）计算时间明显少于普通进化策略算法（ES），从表5知，对于14节点系统SR-ES平均计算时间只有ES的81.5%，明显提高了计算效率。

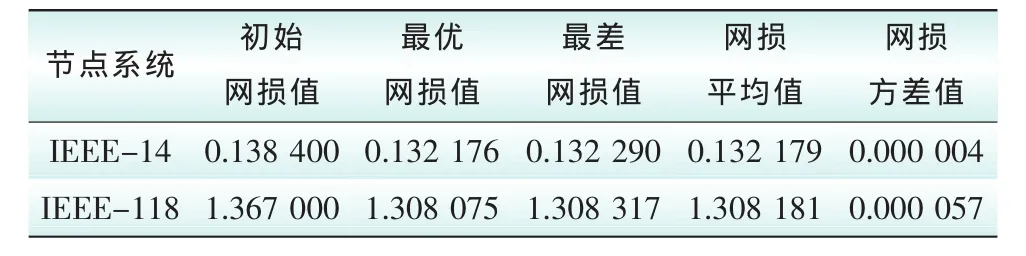
表3 优化后网损情况（30次）Tab.3 Network loss after optimization（30 times）

表4 4种情况下网损情况比较（30次）Tab.4 Comparisons of network loss by four methods（30 times）

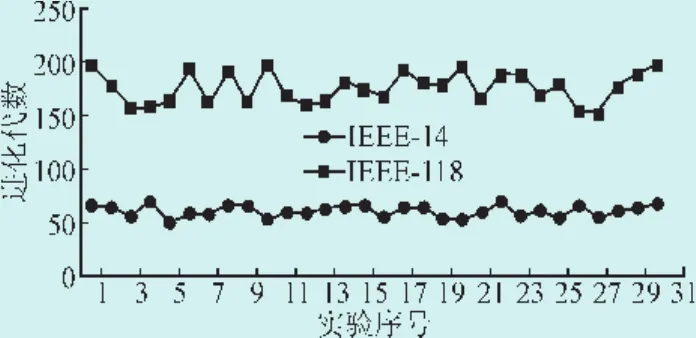
图3 算法进化代数情况Fig.3 The evolution algebra of the improved ES algorithm

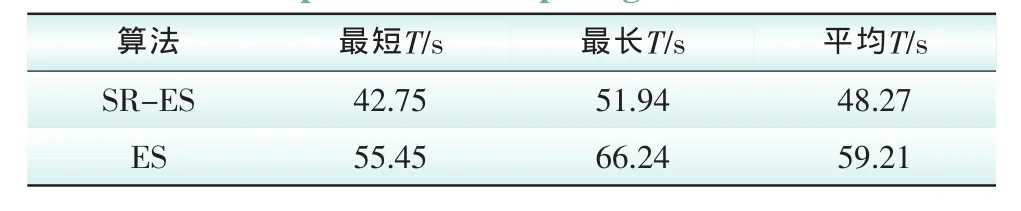
表5 IEEE-14系统计算时间比较Tab.5 Comparison of computing time for IEEE-14

4 结语

本文将带随机排序策略的进化算法应用到无功优化问题中，有效地避免了罚函数法处理约束问题时罚系数难以确定的缺点，并在编码方法、进化终止判据方面做了改进，有效地提高了算法收敛稳定性和计算效率。算例说明了改进算法的有效性。

[1]周晓娟，蒋炜华，马丽丽.基于改进遗传算法的电力系统无功优化[J].电力系统保护与控制，2010（7）:37-41.ZHOU Xiao-juan，JIANG Wei-hua，MA Li-li.Reactive power optimization of power system based on improved genetic algorithm[J].Power System Protection and Control，2010（7）:37-41（in Chinese）.

[2]刘桂龙，王维庆，张新燕，等.无功优化算法综述[J].电网与清洁能源，2011（1）:04-08.LIU Gui-long，WANG Wei-qing，ZHANG Xin-yan，et al.Overview of VAR optimization algorithm[J].Power System and Clean Energy，2011（1）:04-08（in Chinese）.

[3]姚李孝，肖靓，王磊，等.基于改进遗传算法的配电网无功优化[J].电网与清洁能源，2009（4）:24-28.YAO Li-xiao，XIAO Liang，WANG Lei，et al.Reactive power optimization based on improved genetic algorithms in distribution system[J].Power System and Clean Energy，2009（4）:24-28（in Chinese）.

[4]许文超，郭伟.电力系统无功优化的模型及算法综述[J].电力系统及其自动化学报，2003（1）:100-104.XU Wen-chao，GUO Wei.Summarize of reactive power optimization model and algorithm in eletric power system[J].Proceedings of the Chinese Society of Universities for Electric Power System and its Automation，2003（1）:100-104（in Chinese）.

[5]苏玲，赵冬梅，韩静.电力系统无功优化算法综述[J].现代电力，2004（6）:40-45.SU Ling，ZHAO Dong-mei，HAN Jing.Summarization of reactive power optimization algorithm in electric power system[J].Modern Electric Power，2004（6）:40-45（in Chinese）.

[6]盛戈皞，涂光瑜，罗毅.人工智能技术在电力系统无功电压控制中的应用[J].电网技术，2002（6）:22-27.SHENG Ge-hao，TU Guang-yu，LUO Yi.Application of artificial intelligence techniques in reactive power/voltage control of power system[J].Power System Technology，2002（6）:22-27（in Chinese）.

[7]韩敬东，董峰，鞠平.电力系统无功优化规划的进化策略法[J].电力系统自动化，2000（17）:16-19.HAN Jing-dong，DONG Feng，JU Ping.An evolutionary strategy method for reactive power planning of power systems[J].Automation of Electric Power Systems，2000（17）:16-19（in Chinese）.

[8]董峰，鞠平.进化策略方法在电力系统无功优化中的应用[J].河海大学学报：自然科学版，2000（5）:30-33.DONG Feng，JU Ping.Application of evolution strategy methods to reactive power optimization of power systems[J].Journal of Hohai University （Natural Sciences），2000（5）:30-33（in Chinese）.

[9]夏可青，赵明奇，李扬.用于多目标无功优化的自适应遗传算法[J].电网技术，2006（13）:55-60.XIA Ke-qing，ZHAO Ming-qi，LI Yang.A self-adaptive genetic algorithm for multi-objective reactive power optimization[J].Power System Technology，2006（13）:30-33（in Chinese）.

[10]聂宏展，张冰冰，王新，等.基于改进粒子群优化算法的电力市场下的无功优化[J].电网技术，2007（21）:85-90.NIE Hong-zhan，ZHANG Bing-bing，WANG Xin，et al.Research on MPSO algorithm based reactive power optimization in electricity market[J].Power System Technology，2007（21）:85-90（in Chinese）.

[11]程莹，刘明波.含离散控制变量的大规模电力系统无功优化[J].中国电机工程学报，2002（5）：54-60.CHENG Ying，LIU Ming-bo.Reactive-power optimization oflarge-scale power systems with discrete control variables[J].Proceedings of the CSEE，2002（5）:54-60（in Chinese）.

[12]Runarsson T P，Xin Y.Stochastic ranking for constrained evolutionary optimization[J].Evolutionary Computation，IEEE Transactions on，2000，4（3）:284-294.

[13]ABDULLAH N R H，MUSIRIN I，MURTHADA M.Constrained reactive powercontrolusing evolutionary computation technique for static security enhancement[C].//2009 Second International Conference on Computer and Electrical Engineering，Dubai:EECS，2009:612-616.

[14]JOINES J A，HOUCK C R.On the use of non-stationary penalty functions to solve nonlinear constrained optimization problems with GA’s [C]//Proceedings of the first IEEE conference on evolutionary computation，Orlando，Florida：IEEE，1994:579-584.

[15]SCHWEFEL H P.Evolution and Optimum Seeking[M].Berlin:A Wiley-Inter science Publication John Wiley&Sons Inc，1994.

[16]张伯明.高等电力网络分析[M].北京：清华大学出版社，1996：323-328.