静止轨道卫星连续式等间隔脉冲推力东西位置保持策略
2013-05-09常建松李全军
常建松,李全军,袁 勇
(1.北京控制工程研究所,北京 100190;2.空间智能控制技术重点实验室,北京 100190;3.西安卫星测控中心,西安 710043)
中国地球静止轨道卫星在轨管理初期,在位保模式下进行东西位置保持控制,出现喷气次数多、轨控精度差、燃料消耗大、测控时段长等一系列问题,文献[1]针对这一现象,设计了正常模式下由地面控制推力器打脉冲东西位置保持策略,全过程需要在地面监控下执行.随着技术的发展,新型地球静止轨道卫星在正常模式下设计有专门的控制方式和算法用来实施东西位保,地面只需要注入位保控制参数,包括喷气脉宽、喷气周期和喷气次数,星上即可自主完成东西位置保持控制.
但是,上述策略均采用传统的集中式位置保持管理方法,根据卫星定点位置摄动加速度和位置保持环大小,定期进行东西位置保持控制,通常控制周期为2至3周,且每次位保都要进行姿态控制方式转换、控制参数的计算和注入,需要发送大量遥控指令,操作过程十分复杂.因此,本文提出了一种新东西位置保持策略,在正常模式下利用星上控制算法,连续不断地通过等间隔脉冲推力作用,克服卫星所受摄动力的影响,控制卫星东西方向经度位置保持不变.
1 传统东西位置保持控制策略介绍
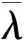
(1)


图1 东西位置保持环
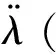
目标轨道的平经度漂移率
(2)
控制周期
(3)
每次控制半长轴改变量
(4)
所需要的速度增量
(5)
其中地球同步轨道半径rs=42164.17km,地球自转角速度ωe=7.2921158×10-5rad/s=360.9856(°)/d.
2 连续式等间隔脉冲推力东西位保策略
2.1 摄动分析
静止轨道卫星在东西方向上的经度漂移主要受地球非球形引力摄动影响.由于地球是质量分布不均匀形状不规则的扁球体,其引力位函数一般形式为[3]

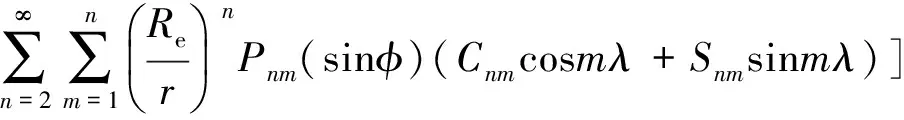
(6)
其中r为地心距,φ为纬度,λ为经度,Re为地球半径,μ为地球引力常数,Jn为带谐项系数,Cnm和Snm为田谐项系数,Pn和Pnm为勒让德多项式.式中的三项可以分别记为
中心引力位
(7)
带谐项引力位
(8)
田谐项引力位

Pnm(sinφ)(Cnmcosmλ+Snmsinmλ)
(9)
当只考虑J2和J22项摄动时,地球引力位函数可以简化成[2]
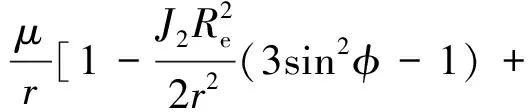
(10)
式中带谐项系数J2=1.08263×10-3,田谐项系数J22=1.81543×10-6,赤道椭圆长轴地理经度λ22=-14.929°.
从式(8)可知,带谐项产生径向和法向摄动,对于地球静止轨道卫星φ≈0,此时法向摄动力约为0,忽略不计.而径向摄动力相当于增大了地球对卫星的中心引力,是长期摄动项,克服长期摄动最简单的办法是调整卫星高度,设考虑地球非球形摄动后的标称静止轨道半长轴为ac,这个值不同于当地球为均匀球体时的同步圆轨道半径as(即rs),定义Δa=ac-as,则根据平经度变化率摄动方程[4]:
(11)

由平均轨道角速度公式,得:


(12)
(13)
只考虑带谐项J2摄动时,沿径向方向的摄动加速度为:
(14)
将式(14)代入式(13),得:
(15)
则带谐项主项J2摄动使标称静止轨道的半长轴增大约2.089km,J2项摄动使卫星发生恒定向东的经度漂移,漂移率为9.77(°)/年.调整卫星轨道高度至标称半长轴ac后,东西位置保持不再考虑带谐项摄动因素,卫星在轨道平面内摄动仅与田谐项有关,东西位置保持控制只需要消除田谐项影响[5].
由式(9)分析可知,对于地球静止轨道卫星,田谐项主要产生径向和切向摄动,其中径向摄动加速度与带谐项相比小得多,可以忽略不计.切向摄动产生加速度使卫星在东西方向漂移,加速度大小与卫星定点位置有关,文献[2]分析二阶田谐项摄动是最主要的,占85%左右,因此对于轨道控制问题仅考虑二阶田谐项即可,沿轨道切线方向的摄动加速度为:
(16)
根据平经度漂移率定义:
平经度漂移加速度
(17)
再根据静止轨道卫星摄动方程,可知:
(18)
最终可以求得:

≈0.00168sin2(λ-λ22)
(19)
2.2 控制策略
假设卫星平经度漂移率为0,采用连续式等间隔脉冲推力方式对卫星实施东西位置保持控制,每天半长轴的控制量等于田谐项摄动加速度引起的半长轴变化量,则卫星平经度可基本保持不变.具体的控制策略如下:
1)采用传统位置保持控制将卫星星下点经度调整至定点位置λs,且半长轴大小为标称静止轨道半长轴ac;
2)在正常模式下,采用连续式等间隔脉冲推力控制方式补偿摄动加速度影响;
3)根据测轨结果,标定推力器实际效率,适时调整补偿量;
4)若卫星平经度漂移至东西保持环边界,则返回步骤1).
该策略相关控制参数计算公式为:
设定卫星质量msat,位保喷气推力Fth,喷气脉宽Pw和喷气效率η,计算一个脉冲推力对轨道半长轴的改变量Δath
(20)

(21)
将克服摄动所需的喷气脉冲次数平均分配到一天中,得到位保喷气周期Pd.
(22)
新策略利用星上正常模式东西位置保持控制算法,仅需要注入喷气脉宽和周期,即可持续地自主完成东西位置保持任务,且注入的控制参数长期有效,不再需要频繁制定位保控制策略,位保过程也不再涉及控制方式的转换,减少了遥控指令,简化了控制流程.新策略将摄动影响平均分配到一天之中控制,每次脉冲喷气控制量小、误差影响小,连续的脉冲推力作用下卫星平经度变化缓慢,位置保持精度高.
2.3 影响分析
新策略通过连续的脉冲推力抵消田谐项引力摄动加速度影响,卫星轨道半长轴基本保持不变.等间隔同方向推力长期作用下沿轨道面平均分布,各次脉冲引起的偏心率变化量相互抵消,其综合控制效果是偏心率基本不受影响,当偏心率在摄动作用下超出保持圆范围时,需要进行专门的偏心率矢量控制操作.东西位保推力方向沿轨道切向,不会改变卫星轨道倾角.根据测轨结果,适时调整补偿量(脉宽或周期),可以确保卫星平经度长期保持在漂移环范围内.
正常模式下实施东西位置保持控制,要考虑轨控推力引起的姿态扰动力矩影响.卫星东西位保使用成对推力器工作,由于推力器的推力差别、推力偏斜及安装误差等原因,会存在对星体的干扰力矩.在干扰力矩影响下,每次轨道控制均会引起姿态变化,因此在执行连续式等间隔脉冲推力东西位置保持控制时,需要选择合适喷气脉宽,使得姿态扰动不会超过控制精度要求.另外干扰力矩最终会被动量轮吸收,当轮子饱和后,需及时地进行角动量卸载,确保动量轮转速在规定范围内.
对于依靠推力器喷气进行角动量管理的卫星,需要根据推力器布局方式,分析喷气卸载对轨道的影响.文献[6]指出使用单个推力器进行喷气卸载时,会改变卫星的平经度漂移率,提出了一种考虑角动量卸载喷气摄动的东西位置保持策略优化方法,有效延长了位保控制周期.若喷气卸载采用力耦控制方式,即通过两个对称推力器同时喷气,姿态控制力矩效果叠加,而轨道切线方向作用力相互抵消,则不影响卫星平经度漂移率,此类卫星不必考虑角动量管理对东西位置保持策略的影响.
2.4 仿真验证

1)半长轴变化趋势
图2为半长轴一年的变化趋势,从图中可以看出连续式等间隔脉冲推力控制方式可以充分消除田谐项摄动加速度影响,一年内半长轴大小基本不变,始终保持在标称静止轨道半长轴ac附近,使得平经度漂移率趋近于0,卫星能够长期保持在定点位置附近.
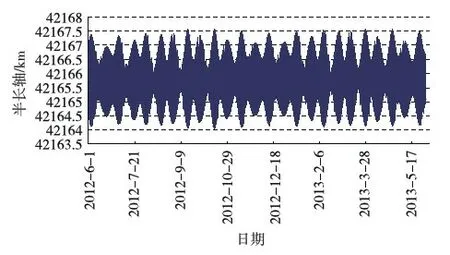
图2 半长轴一年变化趋势
2)偏心率变化趋势
图3与图4分别给出了连续式等间隔脉冲推力控制下与无控制情况下偏心率矢量一年内的变化趋势.从图中可以看出,两者变化规律基本一致,差值小于0.5×10-4,说明连续式等间隔脉冲推力控制基本不改变偏心率矢量变化规律.

图4 偏心率大小一年变化趋势
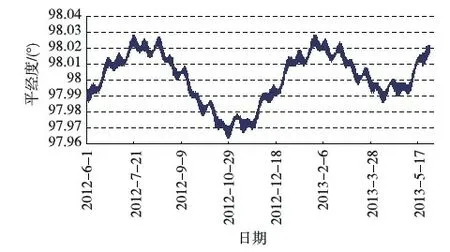
图5 平经度一年变化趋势
3)平经度变化趋势
图5为平经度一年内变化趋势,可以看出平经度始终保持在98°±0.05°范围内.进行连续式等间隔脉冲推力东西位置保持控制时,需根据平经度变化趋势,适时调整补偿量.若观察平经度具有向西漂移趋势,则适当缩短喷气周期,增加喷气次数;反之,若具有向东漂移趋势,则适当延长喷气周期,减少喷气次数.本仿真实例一年内仅微调过3次位保喷气周期,与原来需每2至3周执行一次东西位置保持任务相比,有效减轻了地面测控站工作量.
3 结束语
本文提出的连续式等间隔脉冲推力东西位置保持策略,简化了位保控制流程,减少了地面站操作指令,该策略可以有效地延长东西位置保持控制周期,启动一次控制可以连续工作数月,不再需要频繁地执行东西位置保持任务,极大地减轻了卫星长期管理工作量.
在连续式等间隔脉冲推力作用下,卫星平经度变化十分缓慢,有利于通信卫星的载荷使用,该策略已成功应用于某地球静止轨道通信卫星东西位置保持任务,取得了较好的控制效果,可推广应用到同类型卫星的在轨管理工作中.
参 考 文 献
[1]邓红兵, 李栋林.三轴卫星向西轨道控制策略研究与应用[J].弹箭与制导学报,2003, 23(3): 69-73
Deng H B, Li D L. The research and implementation of a 3-axises geostationary satellite westward longitude maneuver[J]. Journal of Projectiles Rockets Missiles and Guidance, 2003, 23(3): 69-73
[2]章仁为.卫星轨道姿态动力学与控制[M].北京: 北京航空航天大学出版社,1998
[3]杨嘉墀.航天器轨道动力学与控制[M].北京: 宇航出版社,1995
[4]李恒年.地球静止卫星轨道与共位控制技术[M].北京: 国防工业出版社,2010
[5]李于衡.地球静止轨道通信卫星位置保持原理及实施策略[J].飞行器测控学报.2003,22(4): 53-61
Li Y H. The principle of station-keeping and maneuver strategies of geostationary communication satellites[J]. Journal of Spacecraft TT&C Technology, 2003,22(4): 53-61
[6]陈宏,郑军,李于衡.偏置动量卫星东西位置保持策略优化方法[J].上海航天,2011,28(3): 37-41
Cheng H, Zheng J, Li Y H. Optimum strategy of east-west station-keeping for biased momentum satellite[J]. Aerospace Shanghai, 2011, 28(3): 37-41
