基于线性最小均方差估计的星敏感器故障诊断*
2013-05-09何英姿
袁 泉,何英姿,邢 琰,熊 凯
(1.北京控制工程研究所,北京 100190; 2.空间智能控制技术重点实验室,北京 100190)
对1980年到2005年间的156起在轨航天器故障统计显示,大约32%的故障出现在姿态与轨道控制系统,而且其中超过50%的故障是由陀螺、动量轮等姿态测量与控制系统部件引起的[1].因此,很多学者对航天器姿态控制系统的故障诊断方法进行了大量研究[2-4].其中,基于解析模型的故障诊断方法得到了广泛的关注,一般包括残差生成和残差评价两个过程[4].
根据航天器姿态控制系统自身的解析冗余[2],可以通过设计观测器、等价空间等方法获得包含故障特征的残差.通常,用于生成残差的观测器可以分为Luenberger型和Kalman型两种.利用陀螺和红外地球敏感器的冗余关系,文献[5]设计Luenberger型观测器,得到包含敏感器故障信息的残差;文献[6]获得了可以隔离红外地球敏感器与陀螺故障的残差生成器;文献[7]进一步在能观性分解基础上设计奉献观测器,得到隔离不同敏感器故障的残差组.基于Kalman型观测器的航天器姿态控制系统故障诊断残差设计方法可参考文献[8-10].航天器姿态运动学方程具有双线性的形式,是一种简单的非线性系统,其系统噪声以乘性形式出现.文献[11]研究了由星敏感器安装矩阵引起的测量方程中含乘性噪声的滤波问题.文献[12]将基于Luenberger型观测器的残差生成方法推广到双线性系统,并与Kalman型的残差生成器进行了对比分析.
残差评价是从残差中提取故障信息的过程.根据残差生成方法的不同,残差的方向[13]或大小[6]反映了故障信息.对于后者,常对一组残差求取(加权)范数[6,9],再与设定的阈值对比,以确定是否发生故障.阈值一般根据无故障时,残差评价值的近似统计特性,或在某些不确定因素影响下的残差评价值的上界值来确定.
目前,基于解析模型的航天器姿态控制系统故障诊断方法多以陀螺和红外地球敏感器为研究对象[4-7,10].与之相比,以陀螺和星敏感器为诊断对象的研究[8-9]相对较少.此外,在设计用于故障诊断的观测器时,多将对象近似线性化后取加性系统噪声,而对于姿态运动学一类的系统,理论上乘性系统噪声形式的描述更加准确.因此,本文以航天器姿态运动学关系为基础,利用陀螺测量信息与星敏感器的矢量观测信息,并考虑乘性系统噪声的影响,研究星敏感器的故障诊断问题.文章结构安排如下:第一节介绍相关的研究现状,第二节给出姿态运动学模型及星敏感器故障的数学描述,第三节提出基于线性最小均方差的故障诊断算法,第四节为仿真验证.
1 对象模型与问题描述
考虑圆轨道上三轴稳定对地观测航天器,轨道倾角为0°,轨道角速度大小为ωo.轨道参考坐标系OXrYrZr的原点O位于航天器质心,OZr轴沿当地垂线指向地心,OXr轴沿轨道平面与当地水平面的交线指向前进方向,OYr轴垂直于轨道平面并与其余两轴满足右手法则.航天器沿本体主轴方向安装有三正交陀螺,测量本体相对惯性系的角速度; 沿滚动轴和俯仰轴方向安装星敏感器,测量滚动轴方向恒星和俯仰轴方向恒星的单位方向矢量在本体系中的分量.
本节将给出航天器的姿态运动学模型,陀螺和星敏感器的观测模型以及星敏感器的故障模型,其中,小偏差情形下的模型将用于残差生成器的设计问题.
1.1 姿态运动学方程
航天器姿态采用单位四元数[14]表示,即q=[q0q1q2q3]T表示本体坐标系相对惯性坐标系的变换.ω=[ω1ω2ω3]T表示本体系相对惯性系的角速度在本体系中的分量.从而得到航天器姿态运动学模型[14-15]如式(1).

(1)
其中,符号⊗代表四元数乘法[14],类比于复数的表达方式,矢量ω可以看作实部为0的四元数(下同),即ω=0+ω1i+ω2j+ω3k,i,j,k分别表示航天器本体系的坐标轴矢量.
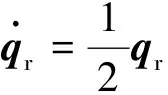


(2)

在小角度下,对式(2)按步长Δt进行一阶离散化,并取k为离散时间变量,可以得到姿态运动学的双线性离散时间模型[12]
(3)
其中,
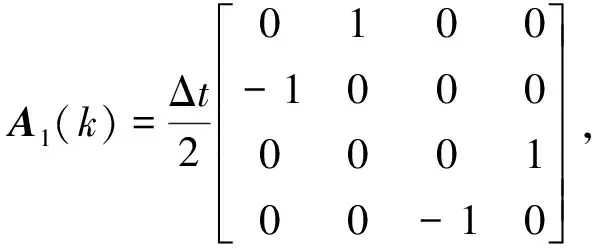

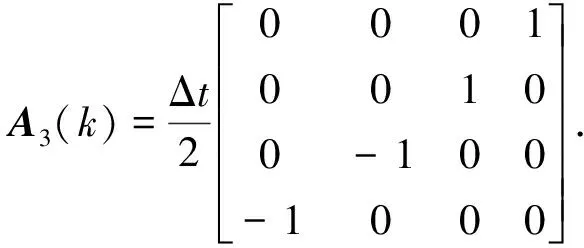
1.2 测量模型
陀螺是航天器上常用的惯性敏感器,提供本体相对惯性系的角速度信息.随着使用时间的增长,陀螺易产生漂移,测量值取为[8]
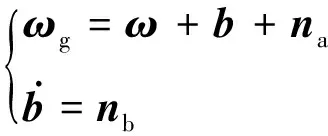
(4)

考虑到一般的姿态测量与确定系统会实时估计陀螺测量偏差b,使其处于较小的区间内,故不失一般性,可以认为仿真初始时b=0.因此,近似的陀螺测量模型可以取为
ωg=ω+na
(5)
星敏感器是高精度姿态敏感器,通过对比测量得到的恒星方向矢量在本体系的分量和由星表提供的恒星方向矢量在惯性系中的分量,来确定航天器本体相对惯性空间的姿态.假定星敏感器识别的恒星沿其光轴方向.记si为任一星敏感器识别的恒星方向单位矢量在惯性系中的分量,记sbm为该恒星方向单位矢量在航天器本体系中的分量.由于不考虑星敏感器的安装误差,因此可以得到该星敏感器的测量值[9]为
(6)
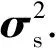
将式(6)改写成误差四元数qe的表示形式
sbm(k)=C(k)qe+ns
(7)

1.3 故障模型
参照式(6),得到星敏感器存在测量偏差式(8)[9]和测量精度逐渐降低式(9)[16]两种故障模型
(8)
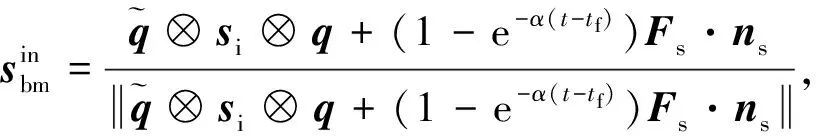
t∈[tf,∞)
(9)



图1 执行机构故障和敏感器故障分离原理
2 基于线性最小均方差估计的诊断算法
2.1 残差生成器
记xqe,uωg,ysbm,由式(2,4,7~9)有

(10)
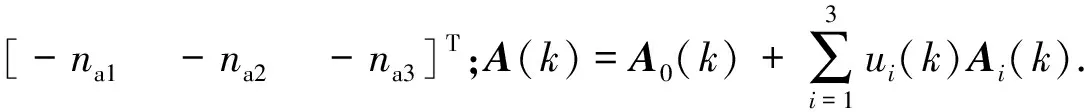
针对无故障情况下的系统(10),设计如下形式的线性最小均方差估计器[17]:



Q(k+1)=A(k)Q(k)AT(k)+
P(k+1)=A(k)P(k)AT(k)+
(11)
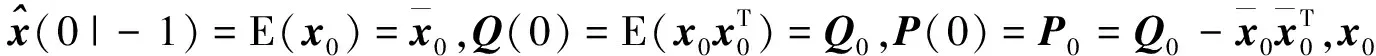
选取残差

(12)
2.2 残差性质分析
取状态估计误差
xe(k)
(13)
则不考虑系统噪声与测量噪声时,由式(10~12),有
r(k)=C(k)A(k)xe(k-1)+f(k)
(14)
xe(k)=(A(k-1)-K(k)C(k)A(k-1))xe(k-1)-
K(k)f(k)
(15)
xe(k)=A(k-1)xe(k-1)-K(k)r(k)
(16)
其中,K(k)=P(k)CT(k)M-1(k)为估计器的增益阵.
首先,分析无故障(f=0)时,残差的收敛问题,分为系统(10)是否满足可观测(或可检测)条件两种情况讨论.
在式(10)满足系统可观测(或可检测)的条件下,由式(11)得到的状态估计误差xe具有依概率E(xe(k))→0,k→∞的特点,且其均方差在统计意义下是所有线性状态估计中最小的[17].从而,由式(12)得到的残差在均方差统计意义下是所有线性反馈增益残差生成器中最优的.
当式(10)不满足系统可观测(或可检测) 的条件时,可将状态变量看作可观(或可检测)和不可观(或不可检测)两部分,此时,由式(11)得到的可观(或可检测)部分的状态估计值的均方差在统计意义下是所有线性状态估计中最小的,而由不可观(或不可检测)的定义(即不可观(或不可检测)状态不会影响观测量)可知,由式(12)生成的残差在均方差统计意义下依然是所有线性反馈增益残差生成器中最优的.
然后分析有故障发生(f≠0)时,残差的收敛问题,并且为了简化分析,不考虑噪声的影响.由无故障情况下的分析知道,只要系统(10)不是完全不可观测的(或完全不可检测的),系统的可观测性(或可检测性)不会影响到由式(12)得到的残差.故不失一般性,认为系统是可观测的(或可检测的).由式(14)可知,故障发生时刻r≈f≠0.由式(15)知,故障会引起状态估计的偏差,且状态估计误差xe与故障f近似满足线性动力学关系.一般地,认为式(16)中的系统矩阵A(k)是稳定且慢时变的,由此可以得到稳态解关系式
(17)
其中,下标ss表示稳态值.至此可以看出,故障会引起残差和状态估计误差偏离零值,并且会在稳定后使得二者的偏离幅值近似满足关系式(17).
2.3 残差评价与阈值
残差评价是从生成的残差中提取故障信息的关键步骤.选择残差加权平方和[6-7,9]形式的残差评价函数
(18)
其中,N是认为选定的数据窗长度.为了减少计算量,实现对故障的快速检测,可以取N=1.此时,Jr表示故障检测时间窗口长度为1的残差的大小.

再参照残差评价函数式(18)的形式,可以由式(19)近似地确定阈值
(19)
其中,n为常数,一般可取3-5.
故障检测逻辑取为
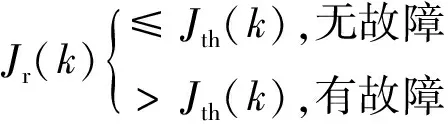
(20)
3 数值仿真
相关仿真参数如表 1所示,动力学与控制相关参数参看文献[15].
故障注入时刻为100s,仿真结果如图2~5.由图2~5可以看出,不论是星敏感器的常值偏差型故障还是精度降低型故障,由以线性最小均方差估计器(式(11))为基础的两个残差生成器(式(11),(12))和相应的残差评价函数(式(13)),阈值(式(14))组成的故障隔离方法可以有效地实现故障隔离.对于常值偏差型故障,残差评价值在故障发生时刻后逐渐降低(图2,4),其出现原因是状态估计误差值对残差值的抵消作用(式(17)); 对于测量精度降低型故障,残差评价值会在故障发生一段时间后才超过设定的阈值(图3,5),其出现原因是故障幅值是缓慢增强的,只有当其幅值达到一定程度后才能成功地检测到.

表1 仿真参数
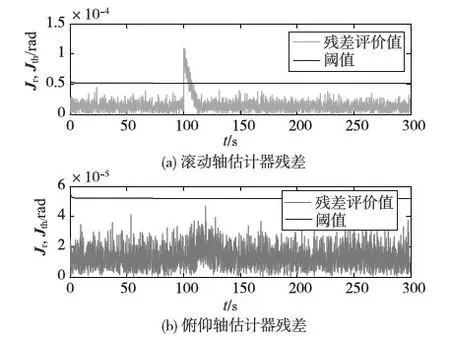
图2 滚动轴方向星敏感器常值偏差情况下故障隔离残差组
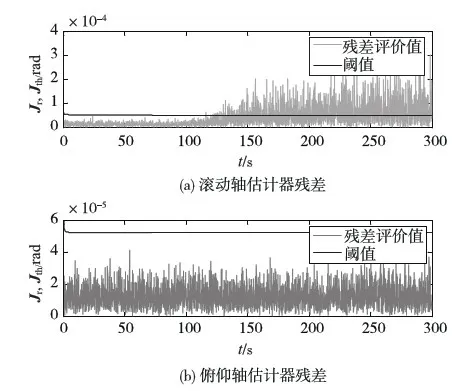
图3 滚动轴方向星敏感器测量精度降低情况下故障隔离残差组

图4 俯仰轴方向星敏感器常值偏差情况下故障隔离残差组

图5 俯仰轴方向星敏感器测量精度降低情况下故障隔离残差组
4 结 论
针对使用两个星敏感器进行姿态测量的姿态控制系统,利用其输出值与陀螺输出值的解析冗余关系,设计两个基于线性最小均方差估计器的残差生成器.通过计算残差评价值,与阈值进行对比,实现了对不同星敏感器的故障隔离.仿真验证了方法的有效性.
本文提出的方法仅要求系统配置可以测量航天器三轴角速度的陀螺和两个测量不共线恒星矢量的星敏感器作为姿态测量部件,而不需红外地球敏感器或太阳敏感器的辅助即可实现星敏感器的故障隔离,且对陀螺和星敏感器的安装角度无特殊限定要求.
参 考 文 献
[1]Tafazoli M. A study of on-orbit spacecraft failures[J]. Acta Astronuatica, 2009, 64: 195-205
[2]Patton R J . Fault detection and diagnosis in aerospace systems using analytical redundancy[J]. Computing & Control Engineering Journal, 1991, 3(2): 127-136
[3]邢琰,吴宏鑫,王晓磊,等.航天器故障诊断与容错控制技术综述[J].宇航学报,2003,24(3): 221-226
Xing Y, Wu H X, Wang X L, et al. Survey of fault diagnosis and fault-tolerant control technology for spacecraft[J]. Journal of Astronautics, 2003, 24(3): 221-226
[4] Marzat J, Piet-Lahanier H, Damongeot F, et al. Model-based fault diagnosis for aerospace systems: a survey[J]. Proc. IMechE Part G: J. Aerospace Engineering, 2012, 226(10): 1329-1360
[5]舒辉旋,秦世引,燕飞.某卫星姿态角的确定和对测量部件的故障诊断[J].航天控制,2007,25(2): 78-81
Shu H X, Qin S Y, Yan F. Attitude determination of a satellite and fault diagnosis for the attitude sensors[J]. Aerospace Control, 2007, 25(2): 78-81
[6]邢琰,吴宏鑫.一种红外地球敏感器和陀螺的故障隔离方法[J].计算技术与自动化,2003,22(2): 74-76
Xing Y, Wu H X. A fault isolation method for infrared earth sensors and gyroscopes[J]. Computing Technology and Automation, 2003, 22(2): 74-76
[7]江耿丰,邢琰,王南华.利用奉献观测器诊断红外地球敏感器故障的新方法[J].航天控制,2007,25(3): 38-42
Jing G F, Xing Y, Wang N H. A new fault diagnosis approach for infrared earth sensors based on dedicated observers[J]. Aerospace Control, 2007, 25(3): 38-42
[8]Mehra R, Seereeram S, Bayard D, et al. Adaptive Kalman filtering, failure detection and identification for spacecraft attitude estimation[C]. The 4thIEEE Conference on Control Applications,Albany, NY, Sept. 28-29, 1995
[9]彭蓉,秦永元.基于多敏感器卫星姿态确定系统故障检测方法研究[J].机械强度,2007,29(3): 487-491
Peng R, Qin Y Y. Research on fault detection method of satellite attitude determination system based on multi-sensors[J]. Journal of Mechanical Strength, 2007, 29(3): 487-491
[10]Xiong K, Chan C W , Zhang H Y . Detection of satellite attitude sensor faults using the UKF[J]. IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(2): 480-491
[11]王炯琦,矫媛媛,周海银,等.适合处理乘性噪声估计卫星姿态的非线性迭代滤波算法[J].电子学报,2011,39(6): 1417-1422
Wang J Q, Jiao Y Y, Zhou H Y, et al. An iterative filter for nonlinear satellite attitude determination system with multiplicative stochastic matrix[J]. Acta Electronica Sinica, 2011, 39(6): 1417-1422
[12]Kinnaert M. Robust fault detection based on observers for bilinear systems[J]. Automatica, 1999, 35: 1829-1842
[13]何英姿,张兵,吴宏鑫.FDF鲁棒决策方法研究[J].宇航学报,1998,19(3): 33-40
He Y Z, Zhang B, Wu H X. The research of FDF robust decision method[J]. Journal of Astronautics, 1998, 19(3): 33-40
[14]Arribas M, Elipe A , Palacios M . Quaternions and the rotation of a rigid body[J]. Celestial Mech Dyn Astr, 2006, 96: 239-251
[15]Sidi M. Spacecraft dynamics and control: a practical engineering approach[M]. Cambridge: Cambridge University Press, 1997
[16]Boem F , Ferrari R M G, Parisini T, Polycarpou M M. A eistributed fault detection methodology for a class of large-scale uncertain input-output discrete-time nonlinear systems[C]. The 50thIEEE Conference on Decision and Control and European Control Conference, Orlando, FL, USA, 12-15, 2011
[17]Costa O L V , Benites G R AM. Linear minimum mean square filter for discrete-time linear systems with Markov jumps and multiplicative noises[J]. Automatica, 2011, 47: 466-476
