一种具有跳跃能力的自平衡两轮机器人动力学建模与越障控制
2013-05-08孙汉旭张延恒贾庆轩
肖 寒,孙汉旭,张延恒,贾庆轩
(北京邮电大学 自动化学院,北京100876)
0 引言
移动机器人作为机器人的一种重要类型,因其相对于固定机器人在功能和应用范围上具有明显优势[1~4],为了扩大星际漫游车的活动范围,NASA曾推出了一系列弹跳机器人[5~8]。美国明尼苏达大学推出一种弹跳机器人UNM Scout[9],可实现跳跃、滚动、停止等动作,哈尔滨工业大学的韩庆虎等人曾研制出一款小型两轮弹跳机器人[10],当其运动时弹跳机构以辅助轮形式拖于地面,需要越障时弹跳机构撞击地面,使两轮机器人越障,取得了不错的越障效果。
自平衡两轮机器人较普通移动机器人具有转弯灵活、无刹车系统及体积小巧[11]等特点,而具备跳跃能力后将会解决其越障能力不足的缺陷。本文针对所研制出的一种具有跳跃能力的自平衡两轮车。本文针对该两轮机器人,建立了其在弹跳准备阶段的动力学模型,并给出了一种模糊滑模控制器实现其自平衡与越障的控制。分析了两轮机器人的最大可控角、起跳条件以及越障条件。规划出机器人在腾空阶段的弹跳轨迹,并给出了落地恢复方案。最后将所设计弹跳控制方案用于两轮机器人弹跳控制中,实验研究验证了所用控制方案的有效性。
1 跳跃准备阶段动力学建模
1.1 机器人越障流程
具有跳跃能力的自平衡两轮机器人见图1,其弹跳越障流程:①根据障碍物外形尺寸规划出机器人跳跃越障的最佳轨迹,确定机器人的起跳速度和角度;②根据确定的起跳角度和速度计算出机器人起跳瞬间所需的水平移动速度和竖直弹跳速度;③设计模糊滑模控制器控制其水平移动速度与弹跳腿角度;④根据所确定的机器人起跳瞬间竖直方向速度控制弹簧的压缩量,实现对竖直速度的控制。
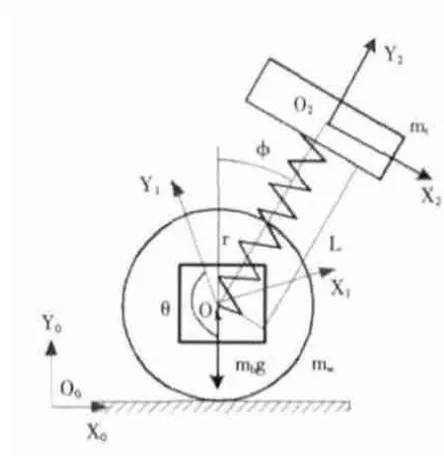
图1 机器人参数定义Fig.1 Robot parameter definition
1.2 动力学建模
由于机器人的弹跳运动过程转向运动会增加系统的不稳定性,而机器人又具有零半径转弯功能,因此在弹跳准备阶段的控制为直线运动控制。机器人的参数定义如图1所示。机器人在地面的直线运动具有两个自由度,分别为车轮滚动角θ,弹跳腿摆角φ,系统输入为长轴电机作用于轮上输入转矩。两轮机器人在运动任意位置处动能计算如下:
其中,mt—弹跳腿上重块质量;mb—机器人底盘质量;mw—机器人两个车轮的质量;r—车轮半径;l—弹跳腿上重块质心到车轮轴线的距离;Jw,Jb,Jt分别为车轮,底盘,上重块相对于车轮轴线的转动惯量。将式 (1)代入拉格朗日方程化简得到:
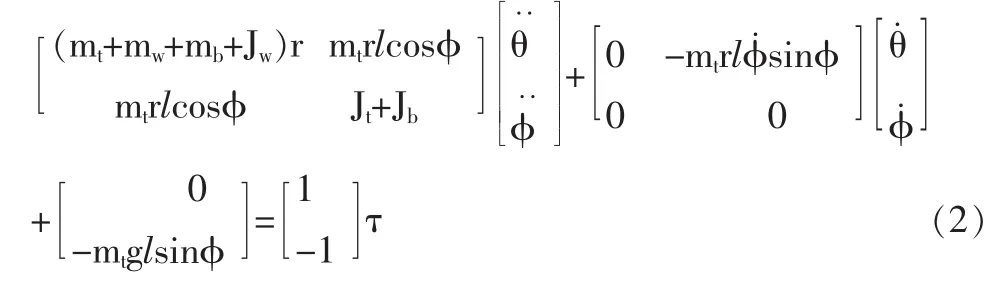
1 .3最大可控角分析
针对所设计机器人,分两种情况分析其最大可控角的影响因素。当机器人处在临界驱动摆角时,电机输入力矩达到最大输入时有:

式中:Mw—此时电机输入力矩,计算可得:

式(4)为此种情况下计算出的最大驱动摆角。而当机器人处在临界驱动摆角时,地面摩擦力为最大滑动摩擦力时有:

式(5)为此种情况下计算出的最大驱动摆角,其中M为机器人整体质量。则机器人的最大可控角为:

由上式看出,可以通过提高电机驱动力矩,增大车轮与地面的摩擦系数,减小偏心质量占机器人总质量比重的办法来增大机器人的最大可控角。
2 跳跃准备阶段模糊滑模控制器设计
将式(2)化为如下的非线性状态空间形式(化简过程略):
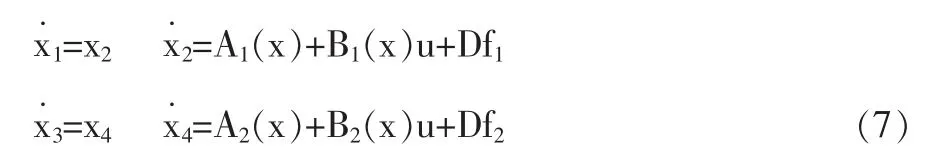
其中,Df1,Df2为未知参数摄动与环境扰动。
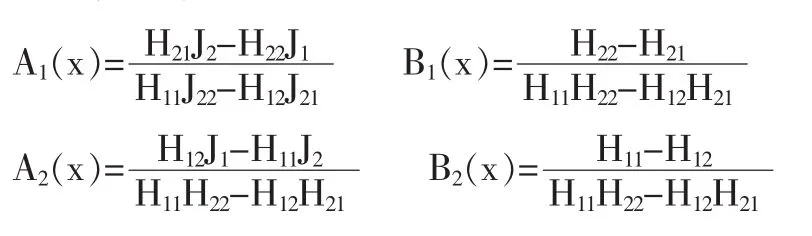


其中:λ2—滑模面S2的系数,也即总滑模面的斜率,通过调整λ2的大小,可以改变总滑模面中两级分滑模面的权重,从而实现了控制优先级的调整。
由于固定不变的λ1,λ2,仅适用于初始条件不变的情况,同时,环境的变化也会造成控制效果的不理想,因此,本文采用模糊在线调整的办法,实现对λ1,λ2的最优配置。将λ1,λ2分别取值如下:
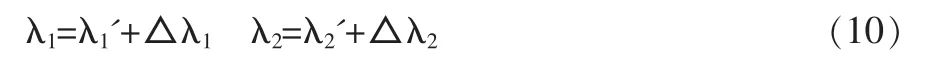
其中,λ1',λ2'—针对系统控制目标,通过遗传算法优化参数所得到的初始值;△λ1,△λ2—模糊控制器输出调整值。
对λ1在线调整构造模糊控制器,输入为弹跳腿摆角φ,输出为△λ1,通过对机器人实物参数的计算可知机器人最大可控角,设为a rad,则取输入论域为(-a,a),输出论域为(-0.3,0.3),隶属度函数取为三角型,模糊控制规则为一一对应。
对λ2在线调整构造模糊控制器,输入为滑模面S1,输出为△λ2,通过对机器人越障参数的计算可知,设定的水平速度为b rad/s,则取输入论域为(0,b),输出论域为(0,0.3),隶属度函数取为三角型,模糊控制规则为一一对应。
所设计模糊滑模控制器最终输出为电机的输入力矩U,此模糊控制器的输入为系统总滑模面函数S及其导数S˙,在此,对传统模糊控制器做一定改进,使其输入输出论域范围可以随当前输入误差做相应调整,以提高模糊控制器的控制精度,我们取滑模面S的输入论域为[-c,c],S˙输入论域为[-d,d],输出力矩 U 的论域为[-c,c],其中 c=1/|2S|,d=1/|2S˙|,相应的隶属度函数取三角型, 模糊控制规则如表1所示。从表中模糊规则的设计可以看出,当S与S˙的取值同号时,模糊规则的控制输出为使S S˙取值减小趋于0,当S与S˙的取值异号时,模糊规则的控制为0,因此SS˙<0时系统趋于稳定,且状态量误差趋于0,由此可见此模糊规则的设计可以满足滑模控制稳定性要求。
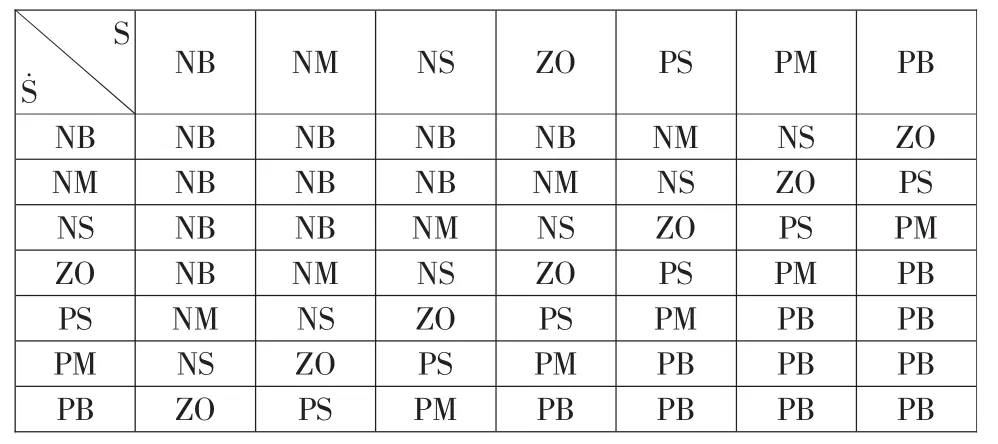
表1 模糊规则表
3 起跳阶段动力学分析
通过控制机器人水平方向与竖直方向运动速度的方法来实现对机器人弹跳角度与速度的控制,弹跳腿维持竖直状态保证系统稳定。机器人在起跳阶段,系统能量守恒:

式中:vty—弹簧恢复原长时弹跳腿以上部分竖直方向的速度;ht—此时上部质心竖直方向上升高度;x—弹簧初始压缩量;k—弹簧劲度系数,由上式可以得出机器人的离地条件为vty>0,计算可得机器人的离地条件为:

弹簧在恢复到原长时,机器人整体锁定,上下部分以相同的速度向上运动,此时由动量守恒有:

v0即为起跳瞬间,机器人的竖直速度,而水平速度为在准备阶段机器人移动速度vx=θ˙r。
4 运动学分析及轨迹规划
要确定机器人在空中的运动轨迹,首先需要根据障碍物外形确定空中运动轨迹的最高点,设机器人在空中运动轨迹抛物线的最高点坐标为(xm,ym),可以解得:

根据机器人所选电机可以确定其最大运动速度为3m/s,由式(14)可以计算出机器人在腾空阶段质心最高点的集合为一实心抛物线。当机器人水平方向速度为最大值,在不同的弹簧压缩量下,机器人质心最高点的轨迹集合为上述实心抛物线的最外层抛物线,而当水平速度不为最大时,则抛物线内的任何一点都可能是跳跃轨迹的最高点。
根据障碍物的类型不同,可以分为沟渠、竖直障碍物以及平台类型障碍物三种,但越障条件均为机器人最低点轨迹高于障碍物。以越过竖直类型障碍物为例,做出如图2所示越障轨迹规划。其中两实心抛物线的相交区域为机器人质心可越障的最高点集合,区域越大,可供选择的越障轨迹方案也就越多,不相交则不可越障。越障轨迹最高点横坐标取0,然后根据起跳点与落地点关于障碍中线对称且保证轨迹与障碍物相离的原则,三点确定出其越障轨迹的抛物线方程。
图2 越障轨迹规划Fig.2 Obstacle navigation trajectory planning
其中起跳点与落地点的选择根据实验所用障碍物所确定的越障轨迹的坐标,实验所选障碍为竖直障碍,高度为15cm,越障轨迹取为距离障碍物最外侧5cm的距离,则由起跳点与最高点坐标可得机器人越障轨迹:

其中最高点坐标为(x0,y0),起跳点坐标为(w,0), w=2r+d/2,d—障碍物宽度。而机器人在水平与竖直方向的运动规律为:
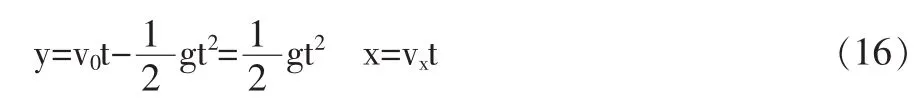

化简可得运动方程为:
由上式的对应项系数相等可以得到:
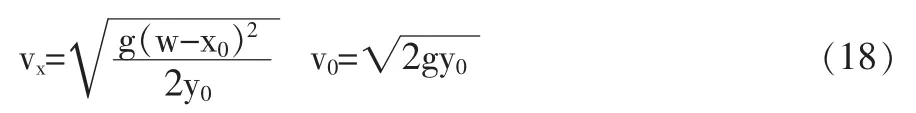
至此,分析得到了机器人在准备阶段与起跳阶段的两个控制目标值,水平速度vx与竖直速度v0。
5 实验
两轮机器人实物的物理参数为mt=1.2kg,mb=0.45kg,mw=0.2kg,r=0.08m,l=0.05m,Jw=0.00064kg·m2,Jb=0.000141kg·m2,Jt=0.003kg·m2, a=0.64rad, b=3rad/s。
实验所用竖直障碍物高度为15cm,设定弹跳高度为20cm,根据前述轨迹规划方法可得规划轨迹方程为:

两轮机器人越障实验过程如图3所示。其实物物理参数与动力学建模参数相同。越障实验机器人水平滚动角速度实验曲线如图4所示,摆角角度曲线如图5所示,从图中可以看出两轮机器人水平速度可以在较短的时间内收敛到期望值,稳态误差极小,摆角及摆角速度也在很短的时间内收敛到0,震荡很小,电机输入力矩无抖振,力矩值在电机最大力矩范围之内,越障运动轨迹符合预期。机器人水平速度、摆角等控制量均可以在较短时间内收敛到期望值,控制效果达到预期,验证了所用控制方法的有效性。

图3 机器人越障实验Fig.3 The robot obstacle navigation experiment
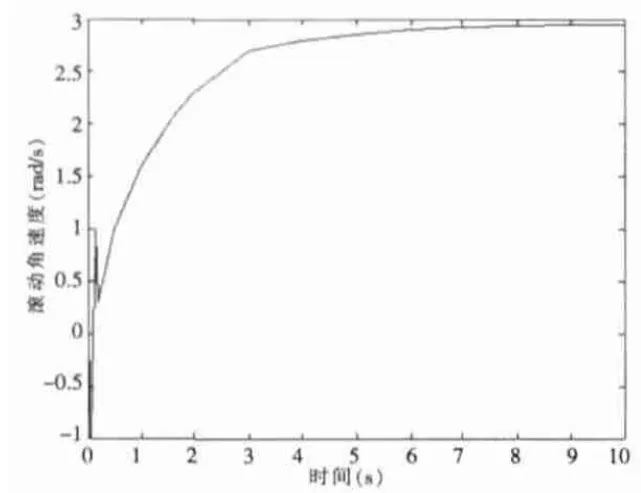
图4 两轮机器人滚动角速度实验曲线Fig.4 Robot rolling angular velocity curves
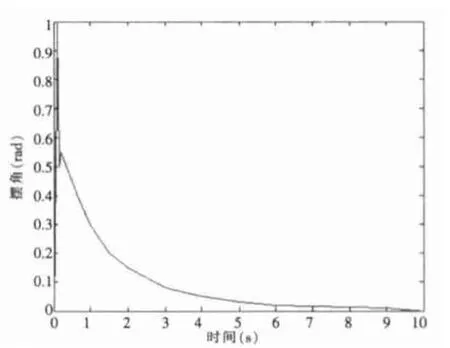
图5 机器人摆角角度实验曲线Fig.5 Robot swinging angle curve
6 结论
本文针对一种具有跳跃能力的两轮机器人的越障控制问题,建立了其动力学模型;利用模糊滑模控制做了机器人弹跳准备阶段的控制;根据障碍物的外形,做了越障轨迹规划,计算得到机器人准备阶段与起跳阶段的控制目标。通过实验验证了所用控制方法具有较好的控制效果,实现了两轮机器人的跳跃越障。
[1]M.H.Kaplan,H.Seifert.Hopping transporters for lunar exploration.Journal of Spacecraft and Rockets.1969,3.
[2]刘壮志,席文明,等.弹跳式机器人研究[J].机器人,2003,6.
[3]刘壮志,朱剑英,吴洪涛.间歇性单足弹跳机器人落地稳定性分析[J].机械科学与技术,2004,9.
[4]刘壮志.弹跳机器人若干关键技术研究[D].南京航空航天大学, 2000,1~5.
[5]Paolo Fiorini,Samad Hayati,Matt Heverly,et al.A Hopping Robot for Planetary Exploration[J].In Proc.of IEEE Aerospace Conf.,March 1999.
[6]E.Hale,N.Schara,J.Burdick,et al.A minimally actuated hopping rover for exploration of celestial bodies[J].In ICRA’2000.
[7]Paolo Fiorini,Joel Burdick.The Development of Hopping Capabilities for Small Robots[J].Auto-nomous Robots,14,2003.
[8]Mirko Confente,Claudio Cosma,Paolo Fiorini,et al.Planetary Exploration Using Hopping Robots[A].7th ESA Workshop on Advanced Space Technologies for Robotics and Automation'ASTRA2002'ESTEC,Noordwijk,the Netherlands,November 19~21,2002.
[9]J.L.Pearce,P.E.Rybski,S.A.Stoeter,N.Papani-kolopoulos.Dispersionbehaviorsforateamofmultipleminiaturerobots.IEEEConferenceonRoboticsandAutomation,Taipei,Taiwan,September,2003.
[10]韩庆虎.小型两轮弹跳机器人的研究[D].哈尔滨工业大学,2007.
